浙江省春晖中学高三数学综合训练试卷（理科）
一、选择题 :（本大题共10小题, 每小题5分, 共50分.）
1．满足条件
1，2
=
的所有集合的个数是 ( )
A．1 B．2 C．3 D．4
2．已知数列
，且
，则 （ ）
(A)
是数列中的项
(B)
是数列中的项
(C)
是数列中的项
(D)
是数列中的项
3．若条件
，条件
，则
是
的 ( )
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．既不充分又不必要条件
4．在等差数列
中，
则前n项和
的最小值为 ( )
A．
B．
C．
D．
5．已知
，
，
与
的夹角为
，如果
，
，则
等于（ ）
A．
B．
C．
D．
6．如果命题P:
, 命题Q:
,那么下列结论不正确的是（ ）
A“P或Q”为真 B．“P且Q”为假 C．“非P”为假 D．“非Q”为假
7.．若直线
被圆
截得的弦长为4，
则
的最小值是 （ ）
A.2
B.4
C.
D.
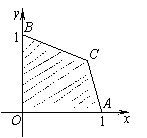
8．如图，目标函数
仅在封闭区域
内（包括
边界）的点
处取得最大值，则
的取值范围是( )
A.
B.
C.
D.
9、函数
的图象大致是
( )
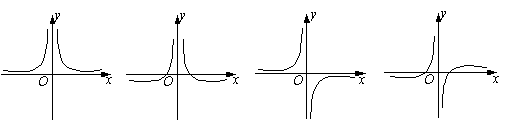
A B C D
10．若
，
，定义
，例如
，则函数
的奇偶性为 （ ）
(A)偶函数 (B)奇函数 (C)既是奇函数又是偶函数 (D)既不是奇函数又不是偶函数
二、填空题:（本大题有4小题, 每小题4分, 共16分.）
11．已知抛物线y=x2+bx+c在点(1,2)处与直线y=x+1相切，则b-c=_________．
12．设等比数列
的前
项和为
，若
，则
等于
．
13．函数
的最大值为 。
14．以下同个关于圆锥曲线的命题中：
①设A、B为两个定点，k为非零常数，
，则动点P的轨迹为双曲线；
②过定圆C上一定点A作圆的动点弦AB，O为坐标原点，若
则动点P的轨迹为椭圆；
③方程
的两根可分别作为椭圆和双曲线的离心率；
④双曲线
有相同的焦点.
其中真命题的序号为 ．（写出所有真命题的序号）
三、解答题 :（本大题有6小题, 共84分. 解答应写出文字说明, 证明过程或演算步骤.）
15.（本小题满分14分）若
，
,
且
，其中Z为整数集,求实数
的取值范围。
16．（本小题满分14分）若
中，a，b，c分别是
的对边，且
，
（1）求
；（2）若
，的面积为
，求b+c的值。
17．（本小题满分14分）已知数列
的前项和为
，数列
满足：
，前项和为
，设
。
⑴ 求数列的通项公式； ⑵ 求证：数列
是单调递减数列；
18．（本小题满分14分）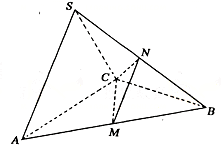
在三棱锥S—ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2
，M、N分别为AB、SB的中点.
（Ⅰ）证明：AC⊥SB；
（Ⅱ）求二面角N—CM—B的大小；
（Ⅲ）求点B到平面CMN的距离.
19.（本题满分14分）定义：离心率
的椭圆为“黄金椭圆”。已知椭圆
：
的一个焦点为
，
为椭圆上的任意一点.
（1）试证：若
不是等比数列，则一定不是“黄金椭圆”；
（2）设E为黄金椭圆，问：是否存在过点F、P的直线L，使L与y轴的交点R满足
？若存在，求直线L的斜率k；若不存在，说明理由。
（3）已知椭圆E的短轴长是2，点S
(0, 2 )，求使
取最大值时点P的坐标。
20．（本小题满分14分）已知
在
上有定义，
，且满足
有
，对数列
，
。
（1）证明：在
上为奇函数；（2）求
的表达式；
（3）是否存在自然数m ,使得对于任意n∈N*，有
成立? 若存在，求出m的最小值。
参考答案
一、选择题：
DDBCB BBCDA
二、填空题：
11．-3 12．512 13．
14．③④
三、解答题：
15．解：．
，
（………………2分）
(1) 当
时,
不符合题意.（…………………5分）
(2当
时,
得
（……………………9分）
(3)当
时,
不符合题意。（…………………12分）
综上所得
（…………………14）
16解：（1）由得：
，
可得：
，
，
。
（2）
，
。
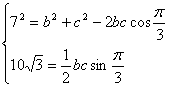
17．⑴ 
，当
时，
∴
⑵ 
∵
∴数列是单调递减数列。
18．解：（Ⅰ）取AC中点D，连结SD、DB.
∵SA=SC，AB=BC，
∴AC⊥SD且AC⊥BD，
∴AC⊥平面SDB，又SB
平面SDB，
∴AC⊥SB.
（Ⅱ）∵AC⊥平面SDB，AC平面ABC，
∴平面SDB⊥平面ABC.
过N作NE⊥BD于E，NE⊥平面ABC，
过E作EF⊥CM于F，连结NF，
则NF⊥CM.
∴∠NFE为二面角N－CM－B的平面角.
∵平面SAC⊥平面ABC，SD⊥AC，∴SD⊥平面ABC.
又∵NE⊥平面ABC，∴NE∥SD.
∵SN=NB，∴NE=SD=
=
=
，且ED=EB.
在正△ABC中，由平几知识可求得EF=MB=，
在Rt△NEF中，tan∠NFE=
=2，
∴二面角N—CM—B的大小是arctan2.
（Ⅲ）在Rt△NEF中，NF=
=
，
∴S△CMN=CM·NF=，S△CMB=BM·CM=2.
设点B到平面CMN的距离为h，
∵VB-CMN=VN-CMB，NE⊥平面CMB，∴
S△CMN·h=S△CMB·NE，
∴h=
=
.即点B到平面CMN的距离为.
（此题也可建空间直角坐标系利用向量求解，略）
19．(I)证明：
假设E为黄金椭圆，则
即
与已知矛盾，故椭圆一定不是“黄金椭圆” 
(II)解：依题假设直线L的方程为
令
点P在椭圆上
,
故
，与
矛盾
所以，满足题意的直线不存在
（III）依题有
，由点P
在E上知
（ⅰ）
故
时取得最大值，此时点P的坐标是（0，-1）
（ⅱ）当
时
时取得最大值，
此时点P的坐标是
20．解：（1）当
=
=0时，
；
令=0，得
即
∴对任意的
，
故在上为奇函数。
（2）∵{
}满足，。∴
，
∵∴
，
在上为奇函数。
∴
；
由，，∴
从而=
。
（3）
=
=
=
假设存在自然数m ,使得对于任意n∈N*，有
成立
即
恒成立。
∴
解得
∴存在自然数，使得对于任意n∈N*，有
成立。
此时，m的最小值为16。