高考浙江省五校联考数学（理）

浙 江 省 五 校 联 考

数学试卷（理科）

本试卷分第Ⅰ卷和第Ⅱ卷两部分。满分150分，考试时间120分钟

第Ⅰ卷

一、选择题：本大题共12题，每小题5分，共60分.在每小题给出的4个选项中，只有一项是符合题目要求的.

1．已知集合可以取的一个值为　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．0　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．1　　　　　　　　　　　　

　　　 C．2　　　　　　　　　　　　　　　　　　　　　　　　　　　　D．3

2．已知l,m为两条直线，则下列条件中可以判断平面平行的是　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　　　　　D．

3．下列函数中是奇函数，且在上为增函数的是　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　B．　　　　

　　　 C．　　　　　　　　　　　　　　　　　　 D．

4．已知△ABC中AB=AC，则下列各式中不一定成立的是　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　 D．

5．某简单多面体有V个顶点和F个面，已知每个面均为四边形，每个顶点上有三条棱.则

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．V=8，F=6　　　　　　　　　　　　　　　　　　　　　B．V=6，F=8

　　　 C．V=8，F=8　　　　　　　　　　　　　　　　　　　　　D．V=6，F=6

6．若复数z满足　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　　　　B．　　　　　　　　　

　　　 C．　　　　　　　　　　　　　　　　　　　　　　　　D．

7．函数的反函数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　B．

　　　 C．　　　　　D．

8．函数　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　　　D．

9．方程满足的性质为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．对应的曲线关于y轴对称　　　　　　　　　 B．对应的曲线关于原点成中心对称

　　　 C．x可以取任何实数　　　　　　　　　　　　　　　 D．y可以取任何实数

10．按一次电视机遥控器上的电源开关，电视机可能出现以下三种情况：①由原来的关机状态转为开机状态；②由原来的开机状态转为关机状态；③电视机保持原来的状态不变.由于电视机从关机状态转为开机状态要等待一段时间，一台电视机处于关机状态时，某人连续按了4次电源开关，结果使电视转为开机，则他所按的4次中可以发生的所有的情况种数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．8　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．12　　　　　　　　　　　

　　　 C．16　　　　　　　　　　　　　　　　　　　　　　　　　　　D．20

11．已知数列当T_n取到最大值时，n的值为　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．9　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．8　　　　　　　　　　　　

　　　 C．8或9　　　　　　　　　　　　　　　　　　　　　　　　 D．7或8

12．已知直线l过点p(2,4)且与抛物线相切于P，若圆C满足下列两个条件：①与直线l切于点P，②与y轴相切.则圆C的方程为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．

　　　 B．

　　　 C．

　　　 D．

第Ⅱ卷

二、填空题：本大题共4小题，每小题4分，共16分.把答案填入答卷纸相应的位置.

13．　　　　　　　　  .

14．某校对全校男女学生共1200名进行健康调查，选用分层抽样法抽取一个容量为200的样本.已知男生比女生多抽了10人，则该校的男生人数应是　　　　　　　　  .

15．若　　　　　　　　  .

16．已知向量“*”的意义为则下列命题①　 ②

③　④中，正确的是　　　　  .

三、解答题：本大题6小题，共74分，解答应这与出文字说明，证明过程或演算步骤.

17．（本小题满分12分）函数

（1）化简f (x)并求出其最小正周期；

（2）f (x)的图象经过怎样的平移变换可以过点？并求出平移后的函数解析式.（只需给出符合条件的一种平移方式及其解析式）

18．（本小题满分12分）已知函数

（1）求f (x)的单调递减区间；

（2）当

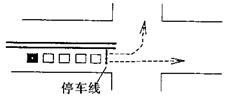
19．（本小题满分12分）如图，一辆车要通过某十字路口，直行时前方刚好由绿灯转为红灯.

该车前面已有4辆车依次在同一车道上排队等候（该车道只可以直行或左转行驶）.已知每辆车直行的概率为，左转行驶的概率.该路口红绿灯转换间隔均为1分钟.假设该车道上一辆直行的车驶出停车线需要10秒，一辆左转行驶的车驶出停车线需要20秒.求：

（1）前面4辆车恰有2辆左转行驶的概率为多少？

（2）该车在第一次绿灯亮起的1分钟内能通过该十字路口的概率（汽车驶出停车线就算通过路口）.

（3）假设每次由红灯转为绿灯的瞬间，所有排队等候的车辆都同时向前行驶，求该车在这十字路口停车等候的时间的数学期望.

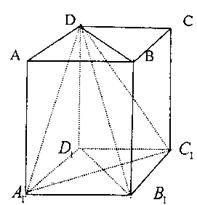
20．（本小题满分12分）直四棱柱A₁B₁C₁D₁—ABCD底面是边长为1的菱形，侧棱长为

（1）求证：平面A₁DC₁⊥平面BB₁DD₁；

（2）若异面直线B₁D与A₁D₁所成角为60°，求二面角A₁—DB₁—C₁的平面角的余弦值；

（3）判断∠DB₁C₁能否为钝角？请说明理由.

21．（本小题满分12分）已知点B（－1，0），C（1，0），P是平面上一动点，且满足

（1）求点P的轨迹C对应的方程；

（2）已知点A（m,2）在曲线C上，过点A作曲线C的两条弦AD，AE，且AD，AE的斜率k₁、k₂满足k₁·k₂=2.求证：直线DE过定点，并求出这个定点.

22．（本小题满分14分）已知数列

（1）求证：

（2）

（3）对于

　　

2004 年 浙 江 省 五 校 联 考

数学试卷（理科）参考答案及评分标准

一、选择题

1	2	3	4	5	6	7	8	9	10	11	12
D	B	B	B	A	C	A	C	D	A	C	B

二、填空题

13．54　　　 14．630　　　　 15．3　　　16．④

三、解答题

17．（1）

（2）方法1.向右平移

方法2：向右平移

（注：答案可有多种）

18．（1）

19．（1）

（2）

（3）设该车在十字路口停车等候时间为t，则时间 t的分布列为

时间t(min)	1	3
概率P

则停车时间的数学期望为

20．（1）∵BB₁⊥平面A₁B₁C₁D₁，A₁C₁平面A₁B₁C₁D₁∴BB₁⊥A₁C₁

又∵A₁B₁C₁D₁为菱形，∴B₁D₁⊥A₁C₁，∴A₁C₁⊥平面BB₁DD_1.

∵A₁C₁平面A₁DC₁，∴平面A₁DC_­1⊥平面BB₁DD₁. …………（3分）

（2）过A₁作A₁H⊥DB₁于H，连HC₁.∵A₁C⊥面BDD₁B₁，∴A₁C₁⊥DB₁，∴DB₁⊥面A₁C₁H，∴HC₁⊥DB₁，∴∠A₁HC₁为二面角A₁—DB₁—C₁的平面角.∵B₁C₁//A₁D₁,∠DB₁C₁（或其补角）为DB₁和A₁D₁所成的角.∴∠DB₁C₁=60°或120°.（5分）

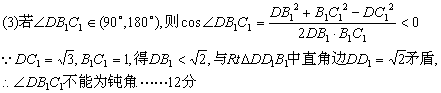
21．（1）设

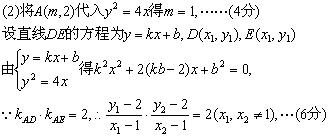
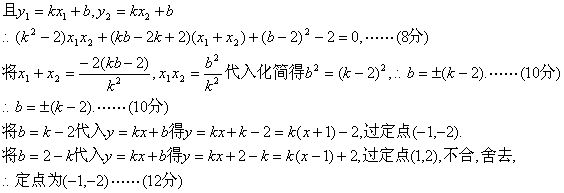22．（1）1°当n=1时，0<a₁<1时,

2°假设n=k时0<a_k<1成立，当n=k+1时，a_k+1=－（a_k－1）²+1，