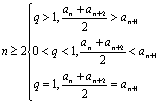高考中国地质大学附属中学高三年级检测试题数学

中国地质大学附属中学2005—2006学年度高三年级检测试题

数 学

一、选择题（本题共12题，总分60分）

1．以T₁，T₂，T₃分别表示函数的最小正

　 周期，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．T₁<T₂<T₃　　　　　 B．T₃<T₂<T₁　　　　　　C．T₂<T₁<T₃　　　　　 D．T₂<T₃<T₁

2．（理）复数z=(m²－4m+3)+(2m²－9m+4)i对应的点Z在第三象限，则实数m的取值范围

　 是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．（2，4）　　　　　　　B．（，4）　　　　　　C．　　D．（1，3）

　（文）设全集U={1，3，5，7，9}，集合A={1，a，9}，　A={5，7}则a的值是（　　）

　　　 A．1　　　　　　　　　　　　B．3　　　　　　　　　　　　C．5　　　　　　　　　　　　D．7

3．（理）已知，则a的值为　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　 D．

　 （文）设x, y∈R，且x+y=4, 则2^x+2^y的最小值是　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．6　　　　　　　　　　　　B．2　　　　　　　　　C．8　　　　　　　　　　　　D．3

4．若等比数列{a_n}中，a₂+a₅+a₁₁=2, a₅+a₈+a₁₄=6，则a₂+a₅+a₈+a₁₁+a₁₄的值为　　　　（　　）

　　　 A．8　　　　　　　　　　　　B．大于8　　　　　　　　 C．　　　　　　　　　D．

5．设a>0，f(x)=x³－ax是上的单调函数，则a的最大值是　　　　　　　　　　　　　 （　　）

　　　 A．0　　　　　　　　　　　　B．1　　　　　　　　　　　　C．2　　　　　　　　　　　　D．3

6．函数f(x)的定义域为[－1，1]，值域为[－3，3]，其反函数为f^－1(x)，则f^－1(3x－2)的（　　）

　　　 A．定义域为，值域为[－1，1]　 B．定义域为，值域为[－3，3]

　　　 C．定义域为，值域为[－1，1]　　　　D．定义域为，值域为[－3，3]

7．已知则　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　　 B．　　　　　　　　

　　　 C．　　　　　　　　　　　　　　　D．

8．函数，若对任意x∈R，都有f(x₁)<f(x)≤f(x₂)成立，则x₁－x­₂的最

　 小值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．4　　　　　　　　　　　　B．2　　　　　　　　　　　　C．1　　　　　　　　　　　　D．

9．过抛物线焦点F的直线与抛物线交于M，N两点，若M，N在抛物线的准线上的射影分

　 别为M₁，N­₁，则∠M₁FN₁等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．30°　　　　　　　　　 B．45°　　　　　　　　　 C．60°　　　　　　　　　 D．90°

10．a, b, c, d ∈R，下列命题正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　 B．

　　　 C．D．

11．已知函数f(x)是R上的减函数，A(0,－2), B(－3,2)是其图象上的两点，那么不等式

f(x－2)>2的解集是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．（－1，2）　　　　　　　　　　　　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　　　　　D．

12．已知直线ax+by+c=0(abc≠0)与圆x²+y²=1相切，则三条边长分别a,b,c 的三角形是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．锐角三角形　　　　B．直角三角形　　　　 C．钝角三角形　　　　D．不存在

二、填空题（本题共4题，共16分）

13．等差数列{a_n}中，a₁+a₂+a₃=15，a_n+a_n－1­+a_n－2=78, S_n=155,则n=　　　　 

14．双曲线 的两个焦点为F₁，F₂，点P在双曲线上，若，则P到x轴的距离为　　　　  

15．设x₁, x₂∈R定义运算×：x₁×x₂=(x₁+x₂)²－(x_­1－x₂)²,若x≥0，常数m>0，则动点

　　P(x, 的轨迹方程是　　　　　　　  

16．已知f(x)=4^x－(k+1)·2^x+2，当x∈R时，f(x)恒为正值，则k的取值范围是　　　　 

三、解答题（本题共6题，共74分）

17．（12分）已知函数

　 （1）求函数f(x)的最小正周期和最大值；

　 （2）作出函数上的图象

18．（12分）已知函数f(x)是定义在R上的周期函数，周期为5，函数y=f(x)在[－1，1]上是奇函数，且在[0，1]上是一次函数，在[1，4]上是二次函数，且在x=2时，取最大值5.

　 （1）求f(1)+f(4)的值；

　 （2）求y=f(x)在[1，4]上的解析式；

　 （3）求y=f(x)在[4，9]上的解析式.

19．（12分）解不等式.

20．（12分）某项希望工程准备兴办一所分校，投资1200万用于硬件建设.为了考虑社会效益和经济利益，对该地区教育市场进行调查，得出一组数据列表（以班为单位）如下：

	班级学生数	配备教师数	硬件建设(万元)	教师年薪(万元/人)
初中	60	2.0	28	1.2
高中	40	2.5	58	1.6

根据有关规定，除书本费、办公费外，初中生每年可收取学费600元，高中生每年可收取学费1500元，因生源和环境等条件限制，办学规模以20对30个班为宜.根据以上情况，请你合理规划办学规模使年利益最大，最大利润是多少万元？（利润=学费收入－年薪支出）

21．（12分）椭圆中心为原点O，焦点F₁，F₂在x轴上，F₁为左焦点，过F₁作斜率为的直线交椭圆于求椭圆方程.

22．（理）（14分）已知数列{a_n}满足

　 （1）求数列{b_n}的通项公式；

　 （2）设数列{b_n}的前项和为S­_n，试比较S_n与的大小，并证明你的结论.

　 （文）数列{a_n}的前n项和S_n，已知S_n是各项为正数的等比数列，试比较

的大小，证明所得的结论.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

数学参考答案

一、选择题：1.C　 2.理D　 文B　　3.理D　 文C　　4.C　 5.D　 6.A　

7.C　 8.B　 9.D　　10.B　　11.C　　12.B

二、填空题：13.10　　  14.　 15.y²=2mx(y≥0)　 16. k<2－1

三、解答题：

17．（1）　 （2）图略

18．（1）0；　 （2）f(x)=－2(x－2)²+5　x∈[1,4]　（3）

19．（1）　　　　　　　　　　　　 （2）

　 （3）a=3, x<0　　　　　　　　　　　　　　　　　　　　　 （4）a>3, <x<0

20．初中班有18个，高中班有12个时，有最大利润为45.6万元.

21．椭圆方程

22．（理）（1）

　 （2）

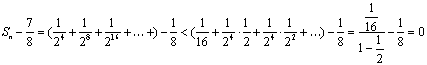
　 （文）