四川省实验中学2005-2006学年度上学期高三统一调研检测
数学试卷
第Ⅰ卷(选择题)
一、选择题：(每小题5分，共60分)
1．已知集合M={(x,y)3x+4y-12<0,x,y∈N°}则集合M的真子集个数是
A.8 B.7 C.6 D.4
2．如果命题“非p或非q”是假命题，则在上列各结论中，正确的为
①命题“p且q”是真命题 ②命题“p且q”为假命题
③命题“p或q”是真命题 ④命题“p或q”为假命题
A.①③ B.②④ C.②③ D.①④
3．对于任意a∈[-1，1]函数f(x)=x +(a-4)x+4-2a的值大于零，那么x的取值范围是
A.(1，3) B.(-∞，1)∪(3，+∞)
C.(1,2) D.(3，+∞)
4.设a>0，a≠1，函数f(x)=log ax-x在[3,4]上是增函数，则a的取值范围是
A.
≤a＜
或a＞1 B.
≤a≤或a＞1
C.a>1 D.
≤a≤或a＞1
5．已知数列{an},“对任意的n∈N+,点Pn (n,an)都在直线y=3x+2上”是“{an}为等差数列”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6．若等比数列{a n}中，a2+a5+a11=2,a5+a8+a14=6,则a2+a5+a8+a11+a14的值为
A.8 B.大于8 C.
D.
7．设sin2x-sin2y=m,则sin(x+y)sin(x-y)的值为
A.m B.-m C.
D.-
8．不等边三角形ABC中，a为最大边，如果a2＜b2+c2那么角A的取值范围是
A.90°<A<180° B.45°<A<90°
C.60°<A<90° D.0°<A<90°
9．已知向量a=(2cosθ,2sinθ),θ∈(
，π),b=(0,-1),则向量a与向量b的夹角α为
A.
-θ B.+θ C.θ- D.θ
10.已知xy=
,0<x<y<1,u=log
xlogy,则
A.u≤1 B.u<1 C.u>1 D.u≥1
11.容器A中有m升水，将水缓慢注入空容器B中，t分钟后容器A中剩余水量y符合指数
函数y=me-at (e=2.718…为自然对数的底数，a是正常数).假设经过5分钟时，容器A和容器B中的水量相等，再经过n分钟时容器A中的水只有 ，则n的值为
A.7 B.8 C.9 D.10
12.对于函数f(x)=
,设f2 (x)=f(f(x)),f3(x)=f(f2(x)),…,fn+1
(x)=f(f(x)).令M={xf2005(x)=x,x∈R}，
则M
A.等于￠ B.等于R
C.为单元素集合 D.为二元素集合
第Ⅱ卷(非选题)
二、填空题：(每题4分，共24分).
13.使集合M={xax2+2x+a=0,a∈R}中有且仅有一个元素的所有a的值组成的集合N为_________________.
14.已知函数f(x)=sinx+5x，x∈(-1,1)，如果f(1-a)+f(1-a2)＜0，则a的取值范围是_____________.
15.已知cosx+cos2x=1,则sin2x+sin8x=__________________.
16.设坐标原点为O，抛物线y2=2x与过焦点的直线交于A、B两点，则
·
等于_________.
17.等差数列{an}的公差不为0，且a1,a2,a4成等比数列，则
=__________________.
18.已知函数f(x)=
，若f(x)=m有一解，则m的范围是__________________.
三、解答题(本大题共5小题，共66分.解答应写出文字说明、证明过程或演算步骤.)
19.(本小题12分)
已知6sin2α+sinαcosα-2cos2α=0,α∈
，求sin(2α+
)的值.
20.(本小题12分)
已知等差数列{an}的前n项和为Sn，且a3=5，S15=225；数列{bn}是等比数列，b3=a2+a3,b2b5=128.
(1)求数列{an}的通项an及数列{bn}的前8项和T8；
(2)求使得
＞成立的正整数n.
21.(本小题14分)
已知ΔABC中，
=(2，3)，
=(1，k)且ΔABC的一个内角为直角，求k值.
22.(本题满分14分)
已知f(x)在(-1,1)上有定义，f(
)=1，且满足当x,y∈(-1,1)时，有f(x)-f(y)=f(
),数列{xn}中有x1=,xn+1=
.
(1)证明：f(x)在(-1，1)上为奇函数；
(2)求f(xn)的表达式；
(3)是否存在自然数m，使得对于任意n∈N+，有 
+
+…+
＜
成立？若存在，求出m的最小值.
23.(本小题14分)
已知函数f(x)=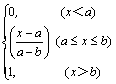
.
(1)证明：对于任意的x≥
，都有f(x)≥
(2)是否存在实数c，使之满足f(c)≥若存在，求出它的取值范围；若不存在，请说明理由.
参考答案
一、（每小题5分）
1．B 2.A 3.B 4.A 5.A 6.C 7.A 8.C 9.A 10.B 11.D 12.A
二、(每小题4分)
13.{-1,0,1} 14.(1,
) 15.3-
16.-
17. 18.m=0或m＞1
三、解答题
19.解：显然cosα≠0故将条件等式两边同除以cos2α，得
6tan2α+tanα-2=0 4分
解得tanα=-
或tanα(舍去). 8分
∴sin(2α+
)=sin2α·cos+cos2α·sin
=sinαcosα+
(cos2α-sin2α) 10分
=
+×
=
+×
=-
+
12分
20.解：(1)设等差数列{an}首项为a1，公差为d，由题意，得：
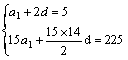2分
解得
∴an=1+(n-1)2=2n-1 4分
设等比数列{bn}的首项为b1,公比为q
∵b3=a2+a3=3+5=8
b2·b5=128
∴
6分
解得
∴bn=2n
∴T8=
=510 8分
(2)∵an=2n-1
∴＞可化为
＞ 10分
解得4＜n＜6
∵n为正整数
∴n=5， 12分
21.解：(1)当∠A=90°时，
=0，
有2×1+3k=0,得k=. 5分
(2)当∠B=90°时，
=(-1,k-3)
=0,
有2×(-1)+3(k-3)=0，得k=
. 10分
(3)当∠C=90°时，
=0，
有-1+k(k-3)=0，
即k2-3k-1=0，解得k=
. 14分
22.(1)证明：当x=y=0时，f(0)=0； 1分
令x=0,得f(0)-f(y)=f(-y)，即f(y)+f(-y)=0 3分
∴对任意的x∈(-1,1)有f(x)+f(-x)=0.
故f(x)在(-1,1)为奇函数. 4分
(2)解：∵{xn}满足x1=，xn+1=
∴0＜xn＜1 6分
∴f(xn)-f(-xn)=f[
]=f
7分
又f(x)在(-1，1)为奇函数
∴f(xn+1)=f(xn)
由f()=1，x1=，有f(x1)=1
从而f(xn)=2n-1 9分
(3)解:
+…+
=1++
+…+
=2- 10分
假设存在自数m，使得对于任意的n∈N+,
有
+
+…+=＜成立，
即2-＜恒成立 11分
∴≥2，解得m≥16 13分
∴存在自然数m≥16,使得对于任意n∈N+，有
++…+=＜成立.
此时，m的最小值为16. 14分
23.解：(1)当x≥时，
①若≤x≤b，则f(x)=
(x-a)2是增函数，故
f(x)≥
=; 3分
②若x＜b,则f(x)=1≥.
故x≥＞1时，f(x)≥成立. 6分
(2)①当a+b≤0时，∵f(x)≥0,
∴对任何c∈R,f(c)≥恒成立； 8分
②当＞1时，∵f(x)≤1，
∴这时c不存在； 10分
③当0＜≤1时，若c≥b，则f(x)=1;
若a≤c≤b时，f(c)=
≥,
解之，得(b-a)
+a≤c≤b
故c≥(b-a)+a，使f(c)≥
. 13分
综上所述，当a+b＞2时，不存在实数c，使f(c)≥;
当a+b≤0时，不存在实数c，使f(c)≥；
当0＜a+b≤2时，c∈
，使f(c)≥. 14分