苏、锡、常、镇四市高三教学情况调查
数 学
第Ⅰ卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么 正棱锥、圆锥的侧面积公式
P(A+B)=P(A)+P(B)
![]()
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B) 其中c表示底面周长,l表示斜高或母线长
如果事件A在一次试验中发生的概率是 球的体积公式
P,那么n次独立重复试验中恰好发生k
![]()
次的概率![]() 其中R表示球的半径
其中R表示球的半径
一、选择题:本大题共12小题,每小题5分,共60分.在每小题的四个选项中,有且只有一项是符合题目要求的.请将正确答案前的字母填在题后的括号内.
1.不等式![]() 的解集是 ( )
的解集是 ( )
A.![]() B.(3,+∞) C.(2,3) D.
B.(3,+∞) C.(2,3) D.![]()
2.设![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
3.设条件A:几何体的各个面都是三角形,条件B:几何体是三棱锥,则条件A是条件B的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
|
|
5.设集合M={a,b,c},N={0,1},映射f:M→N满足![]() ,则映射f:M→N的个数为 ( )
,则映射f:M→N的个数为 ( )
A.1 B.2 C.3 D.4
6.设二项式![]() 的展开式的各项系数的和为P,所有二项式系数的和为S.若有P+
的展开式的各项系数的和为P,所有二项式系数的和为S.若有P+
S=272,则n等于 ( )
A.4 B.5 C.6 D.8
7.圆心在抛物线![]() 上,并且与抛物线的准线及y轴都相切的圆的方程为( )
上,并且与抛物线的准线及y轴都相切的圆的方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.过△ABC的重心任作一直线分别交AB、AC于点D、E.若![]() 则
则![]() 的值为 ( )
的值为 ( )
A.4 B.3 C.2 D.1
9.给出下列四个命题:
(1)各侧面在都是正方形的棱柱一定是正棱柱.
(2)若一个简单多面体的各顶点都有3条棱,则其顶点数V、面数F满足的关系式为2F-V=4.
(3)若直线l⊥平面α,l∥平面β,则α⊥β.
(4)命题“异面直线a、b不垂直,则过a的任一平面与b都不垂直”的否定.
其中,正确的命题是 ( )
A.(2)(3) B.(1)(4) C.(1)(2)(3) D.(2)(3)(4)
10.一个正方体,它的表面涂满了红色.在它的每个面上切两刀,可得27个小立方块,从中任取2个,其中恰有1个一面涂有红色,1个两面涂有红色的概率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.设三棱锥的三个侧面两两互相垂直,且侧棱长均为![]() ,则其外接球的表面积为( )
,则其外接球的表面积为( )
A.48![]() B.36
B.36![]() C.32
C.32![]() D.12
D.12![]()
12.设![]() 是函数F(x)的单调递增区间,将F(x)的图象按a
是函数F(x)的单调递增区间,将F(x)的图象按a![]() 平移得到一个新的函数G(x)的图象,则G(x)的单调递减区间必定是 ( )
平移得到一个新的函数G(x)的图象,则G(x)的单调递减区间必定是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中的横线上.
13.某单位有职工160名,其中业务人员120名,管理人员16名,后勤人员24名.为了解职工的某种情况,要从中抽取一个容量为20的样本,若用分层抽样的方法,抽取的业务人员、管理人员、后勤人员的人数应分别为 .
14.若双曲线![]() 过点
过点![]() ,则该双曲线的焦距为
.
,则该双曲线的焦距为
.
15.某地区预计2004年的前x个月内对某种商品的需求总量![]() (万件)与月份
(万件)与月份![]() 的近似关系式是
的近似关系式是![]() ,则2004年的第x月的需求量g(x)(万件)与月份x的函数关系式是
.
,则2004年的第x月的需求量g(x)(万件)与月份x的函数关系式是
.
16.若直线y=x是曲线![]() 的切线,则a=
.
的切线,则a=
.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
张华同学骑自行车上学途中要经过4个交叉路口,在各交叉路口遇到红灯的概率都是![]() (假设各交叉路口遇到红灯的事件是相互独立的).
(假设各交叉路口遇到红灯的事件是相互独立的).
(1)求张华同学某次上学途中恰好遇到3次红灯的概率.
(2)求张华同学某次上学时,在途中首次遇到红灯前已经过2个交叉路口的概率.
18.(本小题满分12分)
已知函数![]() 的周期为
的周期为![]()
(1)求ω的值.
(2)设△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,求此时函数f(x)的值域.
19.(本小题满分12分)
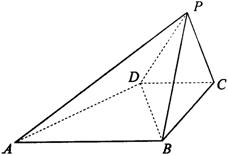
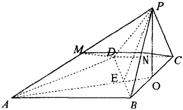
如图,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2CD,侧面PBC⊥底面ABCD.
(1)PA与BD是否相互垂直,请证明你的结论.
|
(3)求证:平面PAD⊥平面PAB.
20.(本小题满分12)
设函数![]()
(1)求函数![]() 的单调区间、极值.
的单调区间、极值.
(2)若当![]() 时,恒有
时,恒有![]() ,试确定a的取值范围.
,试确定a的取值范围.
21.(本小题满分12分)
设二次函数![]() 的所有整数值的个数为g(n).
的所有整数值的个数为g(n).
(1)求g(n)的表达式.
(2)设![]()
(3)设![]() 的最小值.
的最小值.
22.(本小题满分14分)
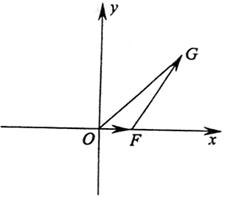
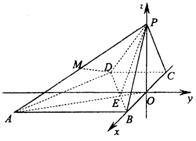
以O为原点,![]() 所在直线为x轴,建立如图所示的直角坐标系.设
所在直线为x轴,建立如图所示的直角坐标系.设![]() 点F的坐标为(t,0),
点F的坐标为(t,0),![]() ,点G的坐标为
,点G的坐标为![]()
(1)求![]() 关于t的函数
关于t的函数![]() 的表达式,判断函数
的表达式,判断函数![]() 的单调性,并证明你的判断.
的单调性,并证明你的判断.
(2)设△OFG的面积![]() ,若以O为中心,F为焦点的椭圆经过点G,求当
,若以O为中心,F为焦点的椭圆经过点G,求当![]() 取得最小值时椭圆的方程.
取得最小值时椭圆的方程.
(3)在(2)的条件下,若点P的坐标为![]() ,C、D是椭圆上的两点,且
,C、D是椭圆上的两点,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
|
数学参考答案
一、选择题
1.D 2.B 3.B 4.C 5.C 6.A 7.C 8.B 9.A 10.C 11.B 12.D
二、填空题
13.15、2、3 14.![]() 15.
15.![]() (注:未写x的取值范围可视作正确) 16.1或
(注:未写x的取值范围可视作正确) 16.1或![]()
三、解答题
17.(1)经过各交叉路口遇到红灯,相当于独立重复试验,所以恰好遇到3次红灯的概率为
![]() …………6分
…………6分
(2)记“经过交叉路口遇到红灯”事件A.
张华在第1、2个交叉路口末遇到红灯,在第3个交叉路口遇到红灯的概率为
![]() …………10分
…………10分
=![]() …………12分
…………12分
18.(1)![]() …………3分
…………3分
由函数![]() 的周期
的周期![]() …………5分
…………5分
函数![]() 的表达式为
的表达式为![]() …………6分
…………6分
(2)由题意,得![]() …………8分
…………8分
又![]() ∴
∴![]() …………9分
…………9分
∴![]() ………………10分
………………10分
∴![]()
即函数![]() 的值域为[-1,
的值域为[-1,![]() ].…………12分
].…………12分
19.解答一:
(1)PA与BD相互垂直.证明如下:
|
连结PO.…………1分 ∵PB=PC,∴PO⊥BC.
又∵平面PBC⊥平面ABCD,
平面PBC∩平面ABCD=BC,
∴PO⊥平面ABCD.…………2分
在梯形ABCD中,可得Rt△ABO≌Rt△BCD,
∴∠BEO=∠OAB+∠DBA=∠DBC+∠DBA=90°,
即AO⊥BD. ∴PA⊥BD. …………4分
(2)连结PE,由PO⊥平面ABCD,AO⊥BD,可得PE⊥BD,…………5分
∴∠PEO为二面角P—BD—C的平面角.………………6分
设AB=BC=PB=PC=2CD=2a,则在Rt△PEO中,PO=![]()
![]() ∴二面角P—BD—C为
∴二面角P—BD—C为![]() …………8分
…………8分
(3)取PB的中点N,连结CN,由题意知:平面PBC⊥平面PAB,则同“(1)”可得CN⊥平面PAB. ………………9分
取PA的中点M,连结DM、MN,则由MN//AB//CD,MN=![]() AB=CD,得四边形MNCD为平行四边形. ∴CN//DM. …………10分 ∴DM⊥平面PAB.…………11分
AB=CD,得四边形MNCD为平行四边形. ∴CN//DM. …………10分 ∴DM⊥平面PAB.…………11分
∴平面PAD⊥平面PAB.………………12分
解答二:
|
△PBC是等边三角形,
得PO⊥底面ABCD.…………1分
以BC中点O为原点,以BC所在直线为x轴,
过点O与AB平行的直线为y轴,
建立如图所示的空间直角坐标系O—xyz.……2分
设CD=1,则在直角梯形中,AB=BC=2,
在等边三角形PBC中,PO=![]() .…………3分
.…………3分
∴A(1,-2,0),B(1,0,0)、D(-1,-1,0)、
P(0,0,![]() ).
).
![]() …………4分
…………4分
(1)PA与BD相互垂直.证明如下:∵![]()
∴![]() …………6分
…………6分
(2)连结AO,设AO与BD相交于点E;连结PE.
由![]() 得
得![]()
又∵AO为PA在平面ABCD内的射影,
∴PE⊥BD,∠PEO为二面角P—BD—C的平面角.…………8分
在Rt△BEO中,OE=OB·![]()
在Rt△PEO中,![]()
∴二面角P—BD—C为![]() ……9分
……9分
(3)取PA的中点M,连结DM,则M的坐标为(![]() ).……10分
).……10分
又![]() ,
,![]() ,
,
∴![]()
![]()
∴![]() ………………11分
………………11分
∴DM⊥平面PAB. ∴平面PAD⊥平面PAB.…………12分
20.(1)![]() …………1分
…………1分
令![]() …………2分
…………2分
由表
| x | a |
| 3a |
| |||
| f′ | - | 0 | + | 0 | - | ||
| f | 递减 |
| 递增 | b | 递减 |
可知:当![]() 时,函数
时,函数![]() 为减函数,当
为减函数,当![]() 时。函数
时。函数![]() 也为减函数;当
也为减函数;当![]() 时,函数
时,函数![]() 为增函数.…………5分
为增函数.…………5分
当x=a时,![]() 的极小值为
的极小值为![]() 时,
时,![]() 的极大值为b.……6分
的极大值为b.……6分
(2)由![]() ……7分
……7分
∵0<a<1, ∴![]() 上为减函数.……8分
上为减函数.……8分
∴![]() …………9分
…………9分
于是,问题转化为求不等式组![]() 的解.…………10分
的解.…………10分
解不等式组,得![]() …………11分
…………11分
又0<a<1, ∴所求a的取值范围是![]() …………12分
…………12分
21.(1)当![]() 时,函数
时,函数![]() 的值随x的增大而增大,则
的值随x的增大而增大,则![]() 的值域为
的值域为![]() …………2分
…………2分
∴![]() …………3分
…………3分
(2)![]() …………4分
…………4分
①当n为偶数时,
![]()
=-[3+7+……+(2n-1)]=-![]() …………6分
…………6分
②当n为奇数时,
![]()
=-![]() ………………8分
………………8分
∴![]()
(3)由![]() , ①
, ①
①×![]() ,得
,得![]() ②…………9分
②…………9分
①-②,得![]()
=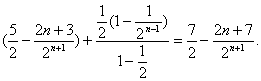
∴![]() ………………11分
………………11分
则由![]() ,可得l的最小值是7.…………12分
,可得l的最小值是7.…………12分
22.(1)由题意知:![]() ………1分
………1分
解得![]() …………2分
…………2分
设![]()
=![]()
∵![]() ∴
∴![]()
函数![]() 在区间[3,+∞)上单调递增.…………4分
在区间[3,+∞)上单调递增.…………4分
(2)由![]() …………5分
…………5分
∴点G的坐标为![]() …………6分
…………6分
∵函数![]() 在区间[3,+∞]上单调递增,
在区间[3,+∞]上单调递增,
∴当t=3时,![]() 取得最小值,此时点F、G的坐标分别为
取得最小值,此时点F、G的坐标分别为
(3,0)、(![]() ).……7分
).……7分
由题意设椭圆方程为![]() …………8分
…………8分
由点G在椭圆上,得![]() 解得b2=9.
解得b2=9.
∴所求椭圆方程为![]() …………10分
…………10分
(3)解答一:设C、D的坐标分别为(x,y)、(m,n),
则![]()
由![]() ………11分
………11分
∵点C、D在椭圆上,∴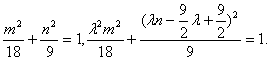
消去m,得![]() …………12分
…………12分
又∵![]() ∴
∴![]() …………13分
…………13分
∴实数λ的取值范围是![]() …………14分
…………14分
解答二:设点A、B的坐标分别为(0,3)、(0,-3),过点A、B分别作y轴的垂线,交直线PC于点M、N.
若![]() ∴1
∴1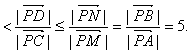
则![]() …………12分
…………12分
若![]() 同理可得
同理可得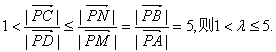 ……13分
……13分
综上,实数λ的取值范围是![]() …………14分
…………14分