襄樊市高三年级统考试题(2004．3)
数学参考答案及评分标准(理工农医类)
一．选择题：ADCBB ACDAA DA
二．填空题：13．1 14．19 15．(p＋0.1)a 16．(1，+∞)
三．解答题：
17．解：a · b
2分
a＋b 
4分
∴cos x≥0，因此 a＋b ＝2 cos x
∴f (x)＝a · b－2
｜a＋b｜即
6分
∴0≤cos x≤1
①若＜0，则当且仅当cos x＝0时，f (x)取得最小值－1，这与已知矛盾； 8分
②若0≤≤1，则当且仅当cos x＝时，f (x)取得最小值
，
由已知得
，解得：
10分
③若＞1，则当且仅当cos x＝1时，f (x)取得最小值
，
由已知得
，解得：
，这与
相矛盾．
综上所述，
为所求． 12分
18．解：取3个球的方法数为
2分
设“3个球全红色”为事件A，“3个全蓝色”为事件B，“3个球全黄色”为事件C，则
，
4分
∵A、B、C为互斥事件 ∴P(A＋B＋C)= P(A)＋P(B)＋P(C)
即 
Þ P(A)＝0 6分
∴红球的个数≤2，又∵n≥2，故n ＝2 8分
记“3个球中至少有一个是红球”为事件D，则
为“3个球中没有红球”
12分
19．(1)解：∵
的第二项为
，∴q＝x 2分
∴an＝xn－1，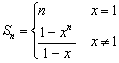
6分
(2)解：当x＝1时，
又
∴
，An＝n · 2 n－1 8分
当x≠1时，
10分
∴
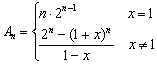12分
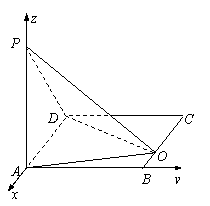
20．方法一
(1)解：以
为x、y、z轴建立空间直角坐标系，则
B(0，
，0)，C(－a，，0)，D(－a，0，0)，P(0，0，4)
2分
设Q(t，，0)，则
＝(t，，－4)，
＝(t＋a，，0)
∵PQ⊥QD，∴
＝0
即t2＋at＋3＝0 ①
∴△＝a2－12≥0 Þ a≥2． 4分
(2)解：∵BC上存在唯一点Q，使PQ⊥QD，
∴△＝a2－12＝0 Þ a＝2，t＝－
6分
＝(－，，0) ，
＝(－2，0，－4)
∴cos
故异面直线AQ与PD所成角为arccos
．
8分
(3)解：过Q作QM∥CD交AD于M，则QM⊥AD，M(t，0，0)
∵PA⊥平面ABCD，∴PA⊥QM，又QM⊥AD，∴QM⊥平面PAD
过M作MN⊥PD于N，连结NQ，由三垂线定理知QN⊥PD
∴∠MNQ是二面角A－PD－Q的平面角
设N (m，0，n)，则
＝(t－m，0，－n)，
＝(t－m，，－n)
＝(－4－m，0，－n)
∵MN⊥PD，ND、PD共线，∴
得：m＋n－t＝0，m－n＝4 ②
由①得：t＝－1或t＝－3，由②得：n＝2＋
t
当t＝－1时，
，当t＝－3时，
∴二面角A－PD－Q的大小为
或
．
12分
方法二
(1)解：设BQ＝t，则PQ2＝19＋t2，QD2＝3＋(a－t)2，PD2＝16＋a2
由PQ⊥QD得：19＋t2＋3＋(a－t)2＝16＋a2，即t2－at＋3＝0 ①
∴△＝a2－12≥0 Þ a≥2．
4分
(2)解：∵BC上存在唯一点Q，使PQ⊥QD，
∴△＝a2－12＝0 Þ a＝2，t＝，故Q是BC中点
取AD中点R，PA中点S，连RS、RC，则RS∥PD，RC∥AQ
∴∠RSC就是异面直线AQ与PD所成角
6分
，
，
∴
故异面直线AQ与PD所成角为arccos．
8分
(3)解：同方法一得∠MNQ是二面角A－PD－Q的平面角
10分
在Rt△PAD中，
在Rt△PQD中，
由①得t＝1或t＝3
当t＝1时，
，当t＝3时，
∴二面角A－PD－Q的大小为或．
12分
21．(1)解：
，∴曲线y＝f (x)在点M (x1，f (x1))处的切线的斜率
∴切线l的方程为
，即
4分
(2)解：令y＝0得
①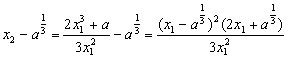
≥0 (*)
∴
，当且仅当
时等号成立． 6分
②∵
，∴(*)中“＝”不成立，故
8分
∵
∴
，故x2＜x1
∴当时，
成立． 12分
22．(1)解：∵a＝xi＋(y＋2)j，b＝xi＋(y－2)j ，且 a ＋ b ＝8
∴点M(x，y)到两个定点F1(0，－2)，F2(0，2)的距离之和为8 2分
∴轨迹C为以F1，F2为焦点的椭圆，方程为
4分
(2)解：
过
轴上的点(0，3)，若直线是轴，则A、B两点是椭圆的顶点
∴
0，∴P与O重合，与四边形OAPB是矩形矛盾． 6分
∴直线的斜率存在，设方程为y＝kx＋3，A(x1，y1)，B (x2，y2)
由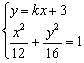
得：
8分
此时，
恒成立，
且
10分
∵
，∴四边形OAPB是平行四边形
若存在直线，使得四边形OAPB是矩形，则OA⊥OB，即
0
∴
12分
即
Þ 
解得：
∴存在直线l：
，使得四边形OAPB是矩形． 14分