朝阳区2002—2003学年第二学期高三综合练习(一)
数 学(文史类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3至8页。共150分,考试时间120分钟。
第Ⅰ卷(选择题,共50分)
参考公式:
|
![]()
![]()
![]()
![]()
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有
一项是符合题目要求.
1.复数![]() 的共轭复数是 ( )
的共轭复数是 ( )
A.1+2i B.![]() C.1-2i D.
C.1-2i D.![]()
2.若a>b>0,集合![]() 表示的集合为 ( )
表示的集合为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.函数![]() 是以
是以![]() 为周期的奇函数,且
为周期的奇函数,且![]() 那么
那么![]() 等于 ( )
等于 ( )
A.![]() B.-
B.-![]() C.1 D.-1
C.1 D.-1
4.设![]() 、b、c为三条不同的直线,
、b、c为三条不同的直线,![]() 、
、![]() 、
、![]() 为三个不同的平面,下面四个命题中真命题的个数是 ( )
为三个不同的平面,下面四个命题中真命题的个数是 ( )
①若![]() ∥
∥![]() ②若
②若![]() ∥
∥![]() .
.
③若![]() 、
、![]() ④若
④若![]() ∥
∥![]()
A.1个 B.2个 C.3个 D.4个
5.已知直线![]() ,在直角坐标平面上,集合
,在直角坐标平面上,集合
![]() 表示 ( )
表示 ( )
A.过l1和l2交点的直线集合 B.过l1和l2交点的直线集合,但不包括直线l2
C.平行直线l1的集合 D.平行直线l2的集合
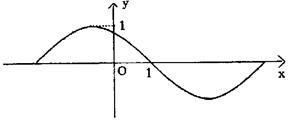
6.如图是周期为![]() 的三角函数
的三角函数![]() 的图象,那么
的图象,那么![]() 可以写成 ( )
可以写成 ( )
|
B.![]()
C.![]()
D.![]()
7.圆周上有12个不同的点,过其中任意两点作弦,这些弦在圆内的交点个数最多是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设椭圆的两焦点分别为(-2,1)、(2,1),两准线间的距离为13,则椭圆的方程是
( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
9.过点(0,2)的直线l与双曲线![]() 的左支交于不同的两点,则直线l的斜率的取值范围是 ( )
的左支交于不同的两点,则直线l的斜率的取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.若函数![]() 的图象关于直线
的图象关于直线![]() 对称,则a的值等于
对称,则a的值等于
( )
A.![]() B.1或-1 C.1或-2 D.-1或2
B.1或-1 C.1或-2 D.-1或2
第Ⅱ卷(非选择题,共100分)
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
11.已知函数![]() 的定义域为R,值域为[1,+∞),则a的值为
的定义域为R,值域为[1,+∞),则a的值为
.
12.直线![]() 截得的弦长为8,则
截得的弦长为8,则![]() 的值为
的值为
.
13.要制造一个底面半径为4cm,母线长为6cm的圆锥,用一块长方形材料做它的侧面,这样的长方形的长与宽的最小值分别是 .
14.抽象函数是由特殊的、具体的函数抽象而得到的.如正比例函数![]() ,
,
![]() 可抽象为
可抽象为
![]() 写出下列抽象函数是由什么特殊函数抽象而成的(填入一个函数即可).
写出下列抽象函数是由什么特殊函数抽象而成的(填入一个函数即可).
| 特 殊 函 数 | 抽 象 函 数 |
|
| |
|
| |
|
| |
|
|
三、解答题:本大题共6小题,共84分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分14分)
已知函数f(x)=![]()
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)解不等式f(x)<0.
16.(本小题满分14分)
已知函数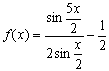
(Ⅰ)将![]() 的整式;
的整式;
(Ⅱ)若![]() 的图象在
的图象在![]() 内至少有一个公共点,试求a的取值范围.
内至少有一个公共点,试求a的取值范围.
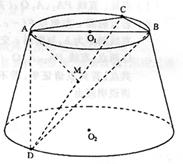
17.(本小题满分14分)
如图,AB是圆台上底面⊙O1的直径,C是⊙O1上不同于A、B的一点,D是下底面⊙
O2上的一点,过D、A、C的截面垂直于下底面,M为DC的中点,AC=AD=2,
∠DAC=120°,
|
(Ⅰ)求证:AM⊥平面DBC;
(Ⅱ)求二面角A—DB—C的正切值;
(Ⅲ)求三棱锥D—ABC的体积.
18.(本小题满分14分)
某加油站需要制造一个容积为![]() 的圆柱形储油罐,已知用来制作底面的铁板每平方
的圆柱形储油罐,已知用来制作底面的铁板每平方
米价格为40元,用来制作侧面的铁板每平方米价格为32元,若不计制作损耗.
(Ⅰ)设储油罐底面半径为x(m),材料成本价为y(元),试用变量x表示y;
(Ⅱ)问储油罐底面半径和高各为多少时,制作的储油罐的材料成本价y最低?
19.(本小题满分14分)
已知函数![]()
(Ⅰ)求![]() 的反函数,并指出其定义域;
的反函数,并指出其定义域;
(Ⅱ)设数列![]() 的前n项和为
的前n项和为![]() ,若对于所有大于1的自然数n都有
,若对于所有大于1的自然数n都有![]() 的通项公式;
的通项公式;
(Ⅲ)令![]()
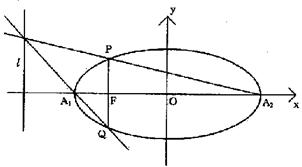
20.(本小题满分14分)
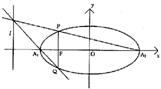
已知:如图,过椭圆![]() 作垂直于长轴A1A2
作垂直于长轴A1A2
的直线与椭圆c交于P、Q两点,l为左准线.
(Ⅰ)求证:直线PA2、A1Q、l共点;
(Ⅱ)若过椭圆c左焦点F(-c,0)的直线斜率为k,与椭圆c交于P、Q两点,直线PA2、A1Q、l是否共点,若共点请证明,若不共点请说明理由.
|
朝阳区2002—2003学年第二学期高三综合练习(一)
数学(文史类)参考答案及评分标准
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| B | C | C | A | D | B | D | A | D | C |
二、填空题
| 11 | 12 | 13 | 14 |
|
|
| 12cm, 9cm | 幂函数 指数函数 对数函数 正切函数 |
三、解答题
15.(Ⅰ)解: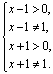 ………………2分 解得:
………………2分 解得:![]() .
.
∴函数f(x)的定义域为![]() ……………………………………4分
……………………………………4分
(Ⅱ)![]()
(1)当![]() …………………………………………………6分
…………………………………………………6分
![]() ∴原不等式显然成立,解为
∴原不等式显然成立,解为![]() ……8分
……8分
(2)当![]() .…………10分
.…………10分 ![]()
∴原不等式变为![]() …………12分
…………12分
∴原不等式解集为![]() ……………………………………14分
……………………………………14分
16.(I)解: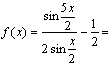
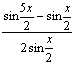 ……2分 =
……2分 =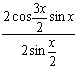 ………4分
………4分
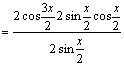 …………6分
…………6分 ![]() ……8分
……8分
![]() …………………………………………………………10分
…………………………………………………………10分
(Ⅱ)解:![]()
![]() …………………12分
…………………12分
![]()
当![]() 内至少有一个公共点.………14分
内至少有一个公共点.………14分
|
∴AM⊥DC……………………2分
∵平面DAC⊥平面ABC,C为圆O1
上异于A,B的一点,则有BC⊥AC,
∴BC⊥平面DAC,故BC⊥AM.…4分
∴AM⊥平面DBC.…………………6分
(Ⅱ)解:作MN⊥DB于N,连接AN,由三垂线
线定理可知AN⊥DB.
∠MNA是二面角A—DB—C的平面角.…………………………………8分
在△ADC中,AC=AD=2,∠DAC=120°∴DC=2![]() ,AM=1.
,AM=1.
由BC⊥平面DAC,可知BC⊥DC.
在Rt△DCB中,DC=2![]() ,∠BDC=30°,可得BC=2,从而MN=
,∠BDC=30°,可得BC=2,从而MN=![]() .
.
 .…10分
.…10分
(Ⅲ)解:![]() ……14分
……14分
18.(Ⅰ)解:设圆柱形储油罐的底面半径为x米,高为h米,材料成本价为y元.
依题意有:![]() …4分
…4分
y=![]() ……6分
……6分
(Ⅱ)解:![]() …………………………8分
…………………………8分
![]() ………………10分 =960π(元).………………12分
………………10分 =960π(元).………………12分
当且仅当![]() 时取等号.
时取等号.
答:当储油罐底面半径为2米,高为5米,材料成本价最低.………14分
19.(Ⅰ)设![]() .…………………2分
.…………………2分
![]()
![]() ……………………………4分
……………………………4分
(Ⅱ)![]()
数列{![]() }是等差数列,公差为
}是等差数列,公差为![]()
![]() ……………………………8分
……………………………8分
当![]()
![]() …………………10分
…………………10分
(Ⅲ)![]()
![]()
![]() ………12分
………12分
![]() .…………………………………14分
.…………………………………14分
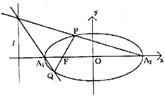
|
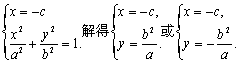
则点P![]() ……………………2分
……………………2分
直线PA2的方程为![]()
![]() …4分
…4分
由方程组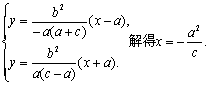 …………………………6分
…………………………6分
因为左准线l的方程为![]() ,所以直线PA2与A1Q的交点在l上.
,所以直线PA2与A1Q的交点在l上.
故直线PA2,A1Q,l相交于一点.………………………………………8分
(Ⅱ)设点P、Q的坐标分别为(![]() .
.
|
直线PA2的方程为![]()
直线A1Q的方程为![]()
![]()
解得交点的横坐标为![]()
即![]() …………………………………………10分
…………………………………………10分
直线PQ的方程为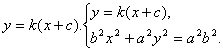
消去![]() (*)
(*)
设M=![]() 方程(*)的二根为
方程(*)的二根为![]()
由韦达定理得:![]() …………………12分
…………………12分
![]() 点P,Q在直线PQ上,
点P,Q在直线PQ上,![]()
![]()
![]()
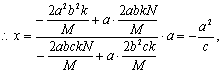 因为左准线l的方程为
因为左准线l的方程为![]() ,所以直线PA2与A1Q的交点在l上.故直线PA2,A1Q,l相交于一点.…………………………14分
,所以直线PA2与A1Q的交点在l上.故直线PA2,A1Q,l相交于一点.…………………………14分