佛山一中远程教育网专题资料之十七：数列的通项与求和
董国强
一. 复习要点
1. 掌握数列通项的求法。
2. 掌握数列求和的方法。
二. 典型例题
1. 求数列的通项的方法
求数列的通项的常用方法有观察法-归纳-证明法、公式法、阶差法、叠乘法、化归法、
待定系数法、特征方程法。
①.归纳-猜测-证明法
由题设条件求出数列的前几项，然后归纳出一般表达式，形成猜想，然后用数学归纳法加以证明，得出正确的结论，是一种重要的思维方法。
例1.已知数列
的前
项和
与通项
的关系是
，其中b是与n无关的常数，且
。
求出用n和b表示的an的关系式。
解析：首先由公式：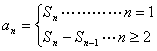
得：
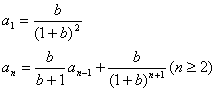
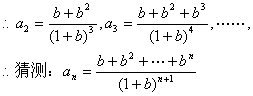
其次，用数学归纳法证明。证明略。
②.公式法
若已知数列的前项和与的关系，求数列的通项可用公式
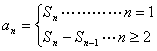求解。
例2. 设数列
的首项为a1=1，前n项和Sn满足关系
求证：数列是等比数列。
解析：因为
所以
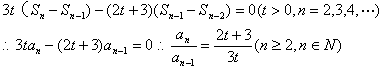
所以，数列是等比数列。
点评：公式的应用要灵活，如本例。
3.阶差法
例3.（本专题例1）已知数列的前项和与的关系是
，其中b是与n无关的常数，且。
求出用n和b表示的an的关系式。
解析：首先由公式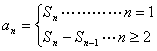：得：
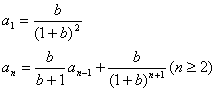
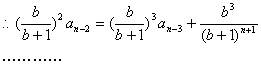
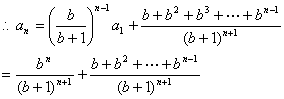
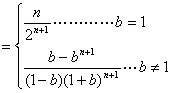
点评：利用阶差法要注意：递推公式中某一项的下标与其系数的指数的关系，即
其和为。
4.叠乘法
例4. 已知数列中，
，前项和与的关系是
，试求通项公式。
解析：首先由易求的递推公式：
将上面n—1个等式相乘得：
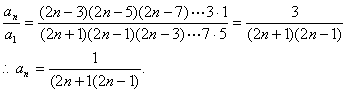
5.化归法
例5. 已知数列中，
，
，
求通项公式。
解析：倒数化归得：
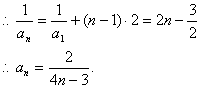
点评：常用的化归还有对数化归，待定化归，一般需转化为等比数列或等差数列的问题。如例1中的
可转化为
令
①
问题①的解决可用待定系数法或特征根法。
⑥ 待定系数法
对于由一阶、二阶或 三阶的线性递推公式求通项问题，均可用待定系数法。
例6. 已知数列
中，
，
，
其中b是与n无关的常数，且
。求出用n和b表示的an的关系式。
解析：递推公式一定可表示为
的形式。
由待定系数法知：
故数列
是首项为
，公比为
的
等比数列，故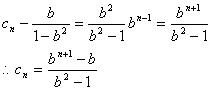
2.数列的求和
等差数列与等比数列的有限项求和总是有公式可求的，其它的数列的求和不总是可求的，但某些特殊数列的求和可采用分部求和法转化为等差数列或等比数列的和或用裂项求和法、错位相减法、逆序相加法、组合化归法，递推法。
① 分部求和法
例1.
已知等差数列的首项为1，前10项的和为145，求
解析：首先由
则：
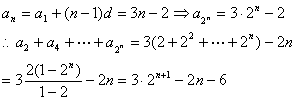
② 裂项求和法
例2. 已知数列为等差数列，且公差不为0，首项也不为0，
求和：
。
解析：首先考虑
则=
点评：已知数列为等差数列，且公差不为0，首项也不为0，下列求和
也可用裂项求和法。
③ 错位相减法
例3.已知
，数列是首项为a，公比也为a的等比数列，令
，求数列
的前项和。
解析：
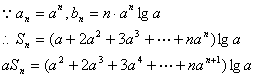
①-②得：
。
点评：设数列的等比数列，数列是等差数列，则数列
的前项和求解，均可用错位相减法。
④ 组合化归法
例4.求和：
。
解析：
而连续自然数可表示为组合数的形式，于是，数列的求和便转化为组合数的
求和问题了。
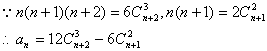
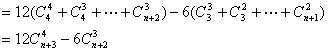
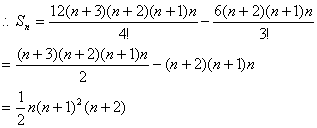
点评：可转化为连续自然数乘积的数列求和问题，均可考虑组合化归法。
⑤ 逆序相加法
例5.设数列是公差为
，且首项为
的等差数列，求和：
解析：因为
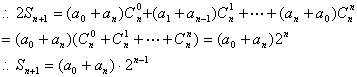
点评：此类问题还可变换为探索题形：
已知数列的前项和
，是否存在等差数列使得
对一切自然数n都成立。
⑥ 递推法
例6. 已知数列的前项和与满足：
成
等比数列，且
，求数列的前项和。
解析：由题意：
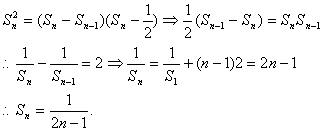
点评：本题的常规方法是先求通项公式，然后求和，但逆向思维，直接求出数列的前项和的递推公式，是一种最佳解法。
三. 高考试题精选
1. （93上海）设数列的前n项和
是常数，且
（1）
证明是等差数列。
（2）
证明以（
为坐标的点
都落在同一条直线上，并写出此直线方程。
（3） 设
是以
为圆心，r为半径的圆
，求使得点P1，P2，P3都落在圆C外时，r的取值范围。
解析：（1）
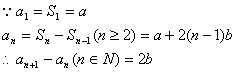
所以，数列是等差数列。
（2）略，（3）详解略，
。
2.（94全国）设数列是正数组成的数列，其前n项和为，并且对于所有的自然数n，与2的等差中项等于与2的等比中项。
（1） 写出数列的前三项。
（2） 求数列的通项公式。
（3） 令
，求
。
解析：（1）由题意：
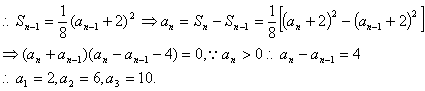
（2）
。
（3）
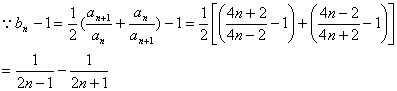
故
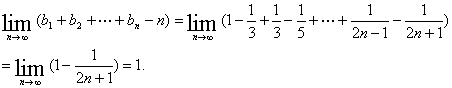
点评：（1）已知数列的前项和与通项的关系时，最好是先转化为递推公式，然后在由递推公式求通项公式。当然，此题也可直接求出前三项，然后猜测通项公式，并用数学归纳法证明。
（2）本题的数列求和采用的是裂项求和法。
3.（89全国）是否存在常数a、b、c，使得等式
，对一切自然数n都成立？
并证明你的结论。
解析：此题的思路有两种：一种是考虑归纳-猜测-证明法。一种是直接求和法。
下面给出一种直接求和法：
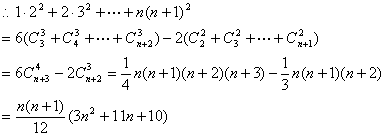
所以，存在常数a、b、c，使得等式
，对一切
自然数n都成立？
4.（99全国春季高考）已知函数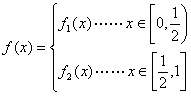
其中
① 画出
的图象。
② 设
的反函数为
，
；求数列
的通项公式。
解析：①略。
②
由待定系数法得：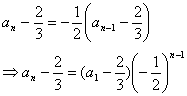
5.（2000广东）设数列为等比数列，
；已知
，
（1） 数列的首项与公比。
（2） 求数列
的通项公式。
解析：（1）易知
。
（3） 采用错位相减法。
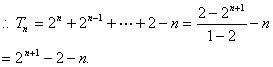
四.过关检测
一. 选择题（满分21分，每小题7分）
a)
已知数列的前项和
，则正确的是
（A）数列是等差数列
（B）数列是等比数列
（C） 数列
是等差数列 （D）数列是等比数列
b)
已知数列的前项和=
，那么
的值是
（A）—3 （B）—1 （C）3 （D）1
c)
数列
的前项和为
二. 填空题（满分28分，每小题7分）
4.求和：
（
）。
5.已知数列是首项为3，公差为2的等差数列，则
）=（ ）。
6.求和：
（ ）。
7.求和：
=（ ）。
三. 解答题 （满分51分）
8.（满分15分）①已知数列满足
求。
②已知数列满足
，求。
9.（满分15分）试问数列
的前多少项的和最大？并求此最大值？
。
10.（满分16分）
正数排成n行n列
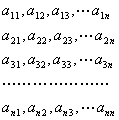
其中每一行的数成等差数列，每一列的数成等比数列，并且所有的公比相等，已知
,求
的值。
参考答案：1C。2B。3B。4.
。5.不存在。6.
。
7.
。
8.略解：（1） 
。
（2）
。
9.略解：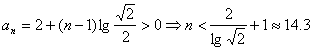
。
故当n=14时，取最大值。
10.略解：依题意，可得方程组
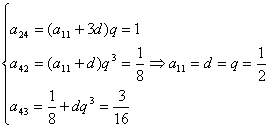
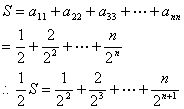
两式相减得：
。
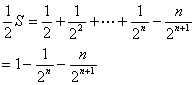
完毕。2001.1.30.