2006高考模拟《导数的应用》选编B
12．（浙江省瓯海中学）已知函数
，
(Ⅰ)若
的图象与
的图象在x=2处的切线互相平行，求a的值；
(Ⅱ)若函数
的两个极值点
恰是方程
的两个根，求a、b的值；并求此时函数的单调区间．
解：
………………1分
（Ⅰ）
…………4分
（Ⅱ）令
分别代入
……7分
………………10分
此时
．．．．．．．．．．．．．．．．．．．．．．．．．．．１４分
13．（重庆市万州区）
已知函数
.
（Ⅰ）
求
；
（Ⅱ）
若
，函数的图象能否总在直线
的下方？说明理由；
（Ⅲ）若函数在
上是增函数，
是方程
的一个根，
求证：
.
解答：（Ⅰ） 
. ………………………2分
（Ⅱ） 时，
，令
得：
由于
，
，
所以函数的图象不能总在直线的下方. ………………………………6分
（Ⅲ）因函数在上是增函数，
在区间上恒成
立，即
在区间上恒成立，
，…………………8分
又由
得
，
而
，
即.………………………12分
14．（2006扬州中学）
已知实数集R上的函数
其中a、b、c、d是实数.
（Ⅰ）若函数在区间
上都是增函数，在区间（－1，3）上是减函数，并且
，求函数的表达式；
（Ⅱ）若a、b、c满足
求证：函数是单调函数
解：
∵函数
在区间
上都是增函数，
在区间（－1，3）上是减函数， ∴－1和3必是
的两个根，
∴
∴
.
（Ⅱ）
由条件
为二次三项式，并且
∴当a>0时，
>0恒成立，此时函数
是单调增函数，
当a<0时，<0恒成立，此时函数是单调减函数，
∴对任意给定的非零实数a，函数
总是单调函数.
15．【莆田四中（二）】
曲线
有极小值，当
处有极大值，且在x =1处切线的斜率为
.
（1）求；
（2）曲线上是否存在一点P，使得y=的图象关于点P中心对称？若存在，请求出点P坐标，并给出证明；若不存在，请说明理由.
解:（1）f′(x)=3ax2+2bx+c
,∵当x=1±
时,f(x)有极小值及极大值
∴f′(1±)=0 即1±为3ax2+2bx+c=0两根
∴b=－3a , c=－6a
又∵f(x)在x=1处切线的斜率为,
（2）假设存在P(x0, y0)，使得f(x)的图象关于P中心对称，则f(x0+x)+f(x0－x)=2y0
即－
(x0+x)3+
(x0+x)2+x0+x－(x0－x)3+(x0－x)2+x0－x=2y0
化解得
，∵对于任意x∈R等式都成立
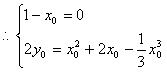∴x0=1, y0=
.易知P（1，）在曲线y=f(x)上.
∴曲线上存在P（1，）使得f(x)的图象关于中心对称
16．[余杭中学（理）]
设定义在正实数集上的两个函数
，
已知g(x)在
上为减函数，
上是增函数
(Ⅰ) 若
为f(x)的导函数,解不等式:
;
(Ⅱ) 证明:方程
上恰有一个实数根.
解：(1)由条件可得:a=2 ----------2分
;
不等式可化为:
------2分
解之得:解集为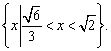
---3分
（Ⅱ）构造函数
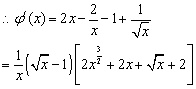--------2分
时,
即
在
上单调递增 ----------2分
又
，
，又在上单调递增，
是其方程的唯一实数根。
-------3分
17．（杭州二中）已知函数
，
（I）设曲线
在点（1，f（1））处的切线为l，若l与圆
相切，求a的值；
（II）若函数在
上是增函数，求a的取值范围．
解：（I）依题意有，
，
过
点的直线的斜率为
，所以，过
点的直线方程为
又已知圆圆心为（－1，0）半径为1，依题意
，解之得
.
（II）
在
上恒成立
，，故
18．已知
是函数
的一个极值点，其中
，且
。
（Ⅰ）求
与
的关系表达式；
（Ⅱ）求的单调区间；
（Ⅲ）当
，
时，函数的图像上任意一点的切线斜率恒大于
，求的取值范围。
（2）、（3）略
19．已知函数
，且函数的图像关于原点对称，其图像在x=3处的切线方程为8x-y-18=0。
（1）求的解析式；
（2）是否存在区间[a，b]，使得函数g（x）的定义域和值域均为[a，b]，且解析式与的解析式相同？若存在，求出这样的一个区间[a，b]；若不存在，请说明理由。
解：（1）
的图像关于原点对称，
恒成立，即
恒成立，
。
，
又的图像在x=3处的切线方程为
，
即
，据题意得：
解得：
，
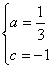…………………6分
（2）由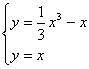
得x=0或
。…………………8分
又
，由
得
，且当
或
时，
，当
时
。
所以，函数在和上递增，在上递减。
于是，函数在
上的极大值和极小值分别为
，
而
，…………………12分
故存在这样的区间[a，b]，其中满足条件的一个区间 …………………14分
20．（临沭县实验中学）
已知函数f(x)=ax3+x2－bx+4(a≠0)在x=1处取到极值。
（1）求a,b满足的关系式(用a表示b)
（2）解关于x的不等式f(x)+2x>1－6ax
（3）问当
时，给定定义域为D=［0,1］时，函数
是否满足对任意的
都有
.如果是,请给出证明；如果不是，请说明理由.
解：(1)由已知得
∵
---------2分
∴3a+2-b=0即b=3a+2 ---------4分
(2)由(1)得b=3a+2
(2)式化为ax3+x2-(3a+2)x+4+2x>-6ax+1 -------6分
∴ax3+x2+3ax+3>0 ∴(ax+1)(x2+3)>0∴ax+1>0 -------8分
∴当a>0时，不等式的解集为
当a<0时，不等式的解集为
-------10分
(3)令
即3ax2+2x-(3a+2)=0 可得x=1或
∵
，∴>1 这时当
时，
当
时,
∴在
时，函数f(x)为减函数----12分
∴当时，
∴对任意，
显然0<1+3a<1,故
总成立
-------14分
21．（临沭县实验中学4）
已知函数
（Ⅰ）若函数在
上恒为单调函数，求实数
的取值范围;
（Ⅱ）设
是函数的两个极值点，若直线AB的斜率不小于
，试求实数的取值范围.
解：（Ⅰ）∵为R上的单调函数，
∴
对
恒成立，（因为
对不恒成立）…2分
∴
，即
………………………………………………………4分
（Ⅱ）∵在
处函数有极值
∴△=
即
或
且
………………………6分
……8分
=
化简得
即
……………………………………11分
∴
……………………………………12分
22．(天津市六校联考)
已知二次函数的二次项系数为，且不等式
的解集为
.
（I）若方程
有两个相等的实数根，求的解析式；
(II)若函数
无极值，求实数的取值范围。
解：(Ⅰ)设
（a≠0），则
…… ①
…… ②
又∵
有两等根
∴
…… ③
由①②③得
又∵
∴a<0, 故
∴
(Ⅱ)
∵g(x)无极值
∴方程
得
23．（钦州市大寺中学3）
已知函数f(x)是在（0，+
）上每一点处可导的函数，若
上恒成立，
（1）求证：函数
上单调递增；
（2）求证：当
1）证明：由g(x)=
′(x)=
由xf′（x）＞f(x)可知：g′(x) ＞0在x＞0上恒成立.
从而g(x)=
…………………………………… 5分
（2）由（1）知g(x)=
在x1＞0,x2＞0时，
……………………9分
于是f(x1)＜
……………………11分
两式相加得到：f(x1)+f(x2)＜f(x1+x2) ……………………………………………12分
24．（无锡市辅仁高级中学）
函数
，过曲线
上的点
的切线方程为
（1）若在
时有极值，求f (x)的表达式；
（2）在（1）的条件下，求
在
上最大值；
（3）若函数在区间
上单调递增，求b的取值范围．
解：（1）
（2）
| x |
| －2 |
|
|
|
|
| + | 0 | － | 0 | + |
|
|
| 极大 |
| 极小 |
|
上最大值为13
（3）
上单调递增
又
依题意
上恒成立.
①在
|
③在
综合上述讨论可知，所求参数b取值范围是：b≥0