2006年普通高等学校招生全国统一考试数学
新型题目汇编及详解
一、选择题(共9题)
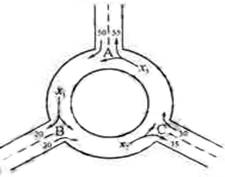 1.(北京卷)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口
1.(北京卷)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口![]() 的机动车辆数如图所示,图中
的机动车辆数如图所示,图中![]() 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段![]() 、
、![]() 、
、![]() 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
解:依题意,有x1=50+x3-55=x3-5,\x1<x3,同理,x2=30+x1-20=x1+10\x1<x2,同理,x3=30+x2-35=x2-5\x3<x2故选C
2. (福建卷)对于直角坐标平面内的任意两点A(x![]() ,
,![]() y
y![]() )、B(x
)、B(x![]() ,y
,y![]() ),定义它们之间的一种“距离”:‖AB‖=︱x
),定义它们之间的一种“距离”:‖AB‖=︱x![]() -x
-x![]() ︱+︱y
︱+︱y![]() -y
-y![]() ︱.给出下列三个命题:
︱.给出下列三个命题:
①若点C在线段AB上,则‖AC‖+‖CB‖=‖AB‖;
②在△ABC中,若∠C=90°,则‖AC‖![]() +‖CB‖
+‖CB‖![]() =‖AB‖
=‖AB‖![]() ;
;
③在△ABC中,‖AC‖+‖CB‖>‖AB‖.
其中真命题的个数为
A.0 B.1 C.2 D.3
解析:对于直角坐标平面内的任意两点![]() ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: ![]() ①若点C在线段AB上,设C点坐标为(x0,y0),x0在x1、x2之间,y0在y1、y2之间,则
①若点C在线段AB上,设C点坐标为(x0,y0),x0在x1、x2之间,y0在y1、y2之间,则![]() =
=![]()
③在![]() 中,
中,
![]() >
>![]()
=![]() ∴命题① ③成立,而命题②在
∴命题① ③成立,而命题②在![]() 中,若
中,若![]() 则
则![]() 明显不成立,选B.
明显不成立,选B.
3.(广东卷)对于任意的两个实数对![]() 和
和![]() ,规定:
,规定:![]() ,当且仅当
,当且仅当![]() ;运算“
;运算“![]() ”为:
”为:![]() ;运算“
;运算“![]() ”为:
”为:![]() ,设
,设![]() ,若
,若![]() ,则
,则![]()
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
解析:由![]() 得
得![]() ,
,
所以![]() ,故选B.
,故选B.
4.(辽宁卷)设+是R上的一个运算, A是R的非空子集,若对任意![]() 有
有![]() +
+![]()
![]() ,则称A对运算+封闭,下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是
,则称A对运算+封闭,下列数集对加法、减法、乘法和除法(除数不等于零)四则运算都封闭的是
(A)自然数集 (B)整数集 (C)有理数集 (D)无理数集
解析: A中1-2=-1不是自然数,即自然数集不满足条件;B中1![]() 2=0.5不是整数,即整数集不满足条件;C中有理数集满足条件;D中
2=0.5不是整数,即整数集不满足条件;C中有理数集满足条件;D中![]() 不是无理数,即无理数集不满足条件,故选择答案C。
不是无理数,即无理数集不满足条件,故选择答案C。
【点评】本题考查了阅读和理解能力,同时考查了做选择题的一般技巧排除法。
5.(山东卷)定义集合运算:A⊙B={z︳z= xy(x+y),z∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为
(A)0 (B)6 (C)12 (D)18
解:当x=0时,z=0,当x=1,y=2时,z=6,当x=1,y=3时,z=12,故所有元素之和为18,选D
6.(陕西卷)为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
A.4,6,1,7 B.7,6,1,4 C.6,4,1,7 D.1,6,4,7
解析:当接收方收到密文14,9,23,28时,
则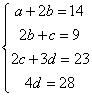 ,解得
,解得![]() ,解密得到的明文为C.
,解密得到的明文为C.
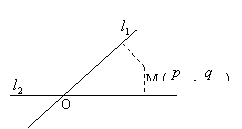
7.(上海卷)如图,平面中两条直线![]() 和
和![]() 相交于点O,对于平面上任意一点M,若
相交于点O,对于平面上任意一点M,若![]() 、
、![]() 分别是M到直线
分别是M到直线![]() 和
和![]() 的距离,则称有序非负实数对(
的距离,则称有序非负实数对(![]() ,
,![]() )是点M的“距离坐标”.已知常数
)是点M的“距离坐标”.已知常数![]() ≥0,
≥0,![]() ≥0,给出下列命题:
≥0,给出下列命题:
 ①若
①若![]() =
=![]() =0,则“距离坐标”为(0,0)的点有且
=0,则“距离坐标”为(0,0)的点有且
仅有1个;
②若![]() =0,且
=0,且![]() +
+![]() ≠0,则“距离坐标”为(
≠0,则“距离坐标”为(![]() ,
,![]() )
)
的点有且仅有2个;
③若![]() ≠0,则“距离坐标”为(
≠0,则“距离坐标”为(![]() ,
,![]() )的点有
)的点有
且仅有4个.
上述命题中,正确命题的个数是 ( )
(A)0; (B)1; (C)2; (D)3.
解:选(D) ① 正确,此点为点![]() ; ② 正确,注意到
; ② 正确,注意到![]() 为常数,由
为常数,由![]() 中必有一个为零,另一个非零,从而可知有且仅有2个点,这两点在其中一条直线上,且到另一直线的距离为
中必有一个为零,另一个非零,从而可知有且仅有2个点,这两点在其中一条直线上,且到另一直线的距离为![]() (或
(或![]() ); ③ 正确,四个交点为与直线
); ③ 正确,四个交点为与直线![]() 相距为
相距为![]() 的两条平行线和与直线
的两条平行线和与直线![]() 相距为
相距为![]() 的两条平行线的交点;
的两条平行线的交点;
8.(上海卷)如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”。在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是
(A)48 (B) 18 (C) 24 (D)36
解析:若空间中有两条直线,若“这两条直线为异面直线”,则“这两条直线没有公共点”;若 “这两条直线没有公共点”,则 “这两条直线可能平行,可能为异面直线”;∴ “这两条直线为异面直线”是“这两条直线没有公共点”的充分非必要条件,选A.
二、填空题(共2题)
9. (上海卷)如图,平面中两条直线![]() 和
和![]() 相交于点
相交于点![]() ,对于平面上任意一点
,对于平面上任意一点![]() ,若
,若![]() 分别是
分别是![]() 到直线
到直线![]() 和
和![]() 的距离,则称有序非负实数对
的距离,则称有序非负实数对![]() 是点
是点![]() 的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是____________.
的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是____________.
解析:正方体中,一个面有四条棱与之垂直,六个面,共构成24个“正交线面对”;而正方体的六个对角截面中,每个对角面又有两条面对角线与之垂直,共构成12个“正交线面对”,所以共有36个“正交线面对”;
10.(四川卷)非空集合![]() 关于运算
关于运算![]() 满足:(1)对任意
满足:(1)对任意![]() 、
、![]() ,都有
,都有![]() ;(2)存在
;(2)存在![]() ,使得对一切
,使得对一切![]() ,都有
,都有![]() ,则称
,则称![]() 关于运算
关于运算![]() 为“融洽集”。现给出下列集合和运算:
为“融洽集”。现给出下列集合和运算:
①![]() {非负整数},
{非负整数},![]() 为整数的加法。
为整数的加法。
②![]() {偶数},
{偶数},![]() 为整数的乘法。
为整数的乘法。
③![]() {平面向量},
{平面向量},![]() 为平面向量的加法。
为平面向量的加法。
④![]() {二次三项式},
{二次三项式},![]() 为多项式的加法。
为多项式的加法。
⑤![]() {虚数},
{虚数},![]() 为复数的乘法。
为复数的乘法。
其中![]() 关于运算
关于运算![]() 为“融洽集”的是
(写出所有“融洽集”的序号)
为“融洽集”的是
(写出所有“融洽集”的序号)
解析:非空集合![]() 关于运算
关于运算![]() 满足:(1)对任意
满足:(1)对任意![]() ,都有
,都有![]() ;
;
(2)存在![]() ,使得对一切
,使得对一切![]() ,都有
,都有![]() ,则称
,则称![]() 关于运算
关于运算![]() 为“融洽集”;现给出下列集合和运算:
为“融洽集”;现给出下列集合和运算:
①![]() ,满足任意
,满足任意![]() ,都有
,都有![]() ,且令
,且令![]() ,有
,有![]() ,所以①符合要求;
,所以①符合要求;
②![]() ,若存在
,若存在![]() ,则
,则![]() ,矛盾,∴ ②不符合要求;
,矛盾,∴ ②不符合要求;
③![]() ,取
,取![]() ,满足要求,∴ ③符合要求;
,满足要求,∴ ③符合要求;
④![]() ,两个二次三项式相加得到的可能不是二次三项式,所以④不符合要求;
,两个二次三项式相加得到的可能不是二次三项式,所以④不符合要求;
⑤![]() ,两个虚数相乘得到的可能是实数,∴ ⑤不符合要求,
,两个虚数相乘得到的可能是实数,∴ ⑤不符合要求,
这样![]() 关于运算
关于运算![]() 为“融洽集”的有①③。
为“融洽集”的有①③。