石狮市2006届高中毕业班质量检查试卷
(文科数学)12月17日
考试时间:120分钟,满分150分
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.已知集合![]() {x
{x![]() x<5},
x<5},![]() {1,2,3,4},则
{1,2,3,4},则![]()
A.{1} B.{1,2} C.{1,2,3} D.{1,2,3,4}
2.点P从(1,0)出发,沿单位圆![]() 逆时针方向运动
逆时针方向运动![]() 弧长到达Q点,
弧长到达Q点,
则Q的坐标是
A.![]() B.(1,0) C.
B.(1,0) C.![]() D.(0,1)
D.(0,1)
3.函数![]() (
(![]() )的反函数是
)的反函数是
A.![]()
![]() B.
B.![]()
![]()
C.![]()
![]() D.
D.![]()
![]()
4.函数![]() 的周期是
的周期是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
5.设![]() 则
则
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.在各项均为正数的等比数列{![]() }中,
}中,![]() ,
,![]() ,则
,则![]() 的值为
的值为
A..2 B. 4 C. 8 D. 64
7.条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的
的
A 充分而不必要的条件 B 必要而不充分的条件
C 充要条件 D 既不充分也不必要的条件
8.若函数![]() 同时具有以下两个性质:①
同时具有以下两个性质:①![]() 是偶函数,②定义域为R,
是偶函数,②定义域为R,
则![]() 的解析式可以是
的解析式可以是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.已知点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,
,![]() ,
,
则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
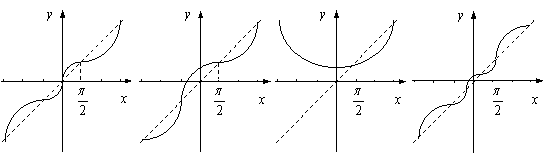 10.函数
10.函数![]() 的大致图象是
的大致图象是
 A.
B. C.
D.
A.
B. C.
D.
11.用32![]() 的铁皮制作一个无盖长方体的盒子,如果底面的宽规定为2
的铁皮制作一个无盖长方体的盒子,如果底面的宽规定为2![]() ,那么这个盒子的最大容积可以是
,那么这个盒子的最大容积可以是
A.36![]() B.24
B.24![]() C.16
C.16![]() D.8
D.8![]()
12.已知数列![]() ,
,![]() =-2[n-
=-2[n-![]() ],
],![]() 为数列
为数列![]() 的前n项和,求
的前n项和,求![]()
某同学作如下解答:∵![]() =-2n+2·
=-2n+2·![]()
∴![]() =-2(1+2+3+4+…+n)+2[(-1)+1+(-1)+1+…]=-2·
=-2(1+2+3+4+…+n)+2[(-1)+1+(-1)+1+…]=-2·![]()
∴![]() =-10×11=-110,
=-10×11=-110, ![]() -99×100=-9900
-99×100=-9900
那么,这位同学的解答情况为
A.![]() 、
、![]() 的值都算对
B.
的值都算对
B.![]() 的值算对,
的值算对,![]() 的值算错
的值算错
C.![]() 的值算错,
的值算错,![]() 的值算对
D.
的值算对
D.![]() 、
、![]() 的值都算错
的值都算错
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上
13.若一个数集中任一元素的倒数仍在该集合中,则称该集合是“可倒”的数集,
例如:![]() 和
和![]() 都是“可倒”的数集.请写出一个“可倒”的数集________;
都是“可倒”的数集.请写出一个“可倒”的数集________;
14.一个田径队有男运动员50人,女运动员40人,用分层抽样方法从全队的
运动员中抽出一个容量为![]() 的样本,则男、女运动员应分别抽取
的样本,则男、女运动员应分别抽取
_________人、________人;
15.已知函数![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
则![]() =_____________;
=_____________;
16.下图中都是由正六边形构成,第①图是一个正六边形,第②图由两个正六
边形构成,第③图由3个正六边形构成,依此类推.则第2006个图中共有
_____________条边.
 |  |  | |||||
三、解答题:本大题共6小题,共74分,解答题应写出文字说明,证明过程或演算步骤:
17.(本小题满分12分)
已知函数![]()
(1)求![]() 的值;
的值;
(2)求使函数![]() 取得最大值或最小值时
取得最大值或最小值时![]() 的集合.
的集合.
18.(本小题满分12分)
已知函数![]()
(1) 解不等式![]()
![]()
(2) 求导函数![]() 及曲线
及曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
19.(本小题满分12分)
已知A(-2,5),B(2,3),C(1,2),
(1)求证△ABC是直角三角形;
(2)数列![]() 中,若
中,若![]()
![]() ,
,![]()
![]() ,且
,且![]()
![]()
①求数列![]() 的通项公式, ②求数列
的通项公式, ②求数列![]() 的前
的前![]() 项中所有偶数项之和.
项中所有偶数项之和.
20.(创新题)(本小题满分12分)
设有米袋100包堆迭成下图的形式(往上一层都比它下面一层少放一些),现要将
这100包全部放好。
(1)如果最下面一层放20包,那么至少有几层?
(2)最下面一层的包数最少可以是多少?
(参考数据:![]() ,
,![]() )
)
21.(本小题满分12分)
定义在R上的函数![]() 满足
满足![]() 时,
时,![]() ,且对任意
,且对任意![]() ,都有
,都有![]() .
.
(1)求![]() ;
;
(2)求证:![]() 为奇函数;
为奇函数;
(3)若![]() ,求实数
,求实数![]() 的所有可能的值.
的所有可能的值.
22(本小题满分14分)
平面向量![]() ,
,![]() ,其中
,其中![]() 为互相
为互相
垂直的单位向量,已知![]() .
.
(1) 当![]() 时,求
时,求![]()
![]() 的范围;
的范围;
(2) 设![]() ,对于给定的负数
,对于给定的负数![]() ,有一个最大的正数
,有一个最大的正数![]() ,使得
,使得
![]()
![]() 时都有
时都有![]() ,问
,问![]() 为何值时
为何值时![]() 最大?求出这个
最大?求出这个
最大的![]() .证明你的结论.
.证明你的结论.
参考答案
一.选择题DADB CCAD ABCB
二.填空题
(13)如![]()
![]() 等等,(14)15, 12, (15)
等等,(14)15, 12, (15)![]() ,(16)10031
,(16)10031
三 解答题(每题只给出一种答案,其他答案仿此给分)
(17)(1)![]() 2分
2分
=![]() 4分
4分
![]() 6分
6分
或![]() 2分
2分
![]() =2
6分
=2
6分
(2) 由![]() =
=![]() 知
知
函数![]() 的最大值是
的最大值是![]() 10分
10分
由![]()
得![]() 12分
12分
所求集合是![]()
(18)(1)![]() 2分
2分
![]() 4分
4分
得![]() 或
或![]() 6分
6分
所以,不等式的解集为![]()
(2)由![]()
![]() 8分
8分
![]() ,
9分
,
9分
又![]() ,
10分
,
10分
即过点M的切线的斜率为-4
根据直线方程的点斜式,过点M的切线方程为
![]() 12分
12分
即![]()
(19)(1)![]()
![]() 1分
1分
![]() 2分
2分
![]()
![]() 4分
4分
![]()
![]() .
5分
.
5分
![]() △ABC是直角三角形.
6分
△ABC是直角三角形.
6分
(2) ![]()
![]()
![]()
![]() 7分
7分
![]()
![]() 8分
8分
当![]() 为偶数时
为偶数时![]() 的偶数项的和为
的偶数项的和为![]() 10分
10分
当![]() 为奇数时
为奇数时![]() 的偶数项的和为
的偶数项的和为![]() 12分
12分
20(1) 事实上20+19+18+17+16+10=5![]() 18+10=100
18+10=100
所以顶层是10包 6分
(2) 设最下面一层放n包,从下往上跌直到最上一层只有一包,此时总包数
是![]() 8分
8分
由 ![]() 9分
9分
得![]()
解得![]() 11分
11分
又![]() 所以满足上式的最小值
所以满足上式的最小值![]() 的值是
的值是![]() 12分
12分
21 (1)令x=y=0,则f(0)=f(0)+f(0),可得f(0)=0… 3分
(2)![]() 对任意的x,y
对任意的x,y![]() R时,恒有f(x+y)=f(x)+f(y)
R时,恒有f(x+y)=f(x)+f(y)
令y=-x可得f(x)+f(-x)=f(x-x)=0
即f(-x)=-f(x)…… 6分
![]() f(x)是奇函数
f(x)是奇函数
(3) f(x) 在(-![]() ,+
,+![]() )上是增函数。事实上:设
)上是增函数。事实上:设![]() ,
,![]()
![]() (-
(-![]() ,+
,+![]() )且
)且![]() >
>![]() 则 f(
则 f(![]() )-f(
)-f(![]() )=
)=![]()
又x>0 时,恒有f(x)>0
![]() f(
f(![]() )-f(
)-f(![]() )>0
)>0
即f(![]() )<f(
)<f(![]() )
)
![]() f(x) 在(-
f(x) 在(-![]() ,+
,+![]() )上是增函数
10分
)上是增函数
10分
于是![]()
可得![]() 11分
11分
所以![]() 12分
12分
22.由![]() 得
得![]()
所以![]() 1分
1分
即![]()
(1)当![]() 时
时 ![]() 2分
2分
当![]() 时,
时,![]() 时取“=”
时取“=”
当![]() 时,
时,![]() 时取“=”
时取“=”
![]() 的范围是
的范围是![]() 4分
4分
(2)![]() ,
,
又![]()
所以![]() 5分
5分
①![]() 时
时
![]()
所以![]() 是方程
是方程![]() 的较小根
的较小根
![]()
![]() 9分
9分
②![]() 时
时
![]() 所以
所以![]() 是方程
是方程![]() 的较大根
的较大根
![]()
![]()
当且仅当![]() 时等号成立,
13分
时等号成立,
13分
由于![]() 因此当且仅当
因此当且仅当![]() 时
时
![]() 的最大值是
的最大值是![]() 14分
14分