2005—2006学年度河南省开封高中高三年级三次月考
数学试卷（文）
YCY
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分300分，考试时间150分钟。
一、选择题（每题5分，共60分）
1．已知
（ ）
A．一个点 B．
C．
D．
A．12 B．10 C．8 D．
4．已知函数
的定义域为R，值域为[－2，2]，则函数
的最大值和最小值分别为 （ ）
A．1，－1 B．2，－2 C．3，－1 D．1，－3
5．已知函数
的反函数为
，则
的定义域为（ ）
A．（－2，0） B．[－1，2] C．[－2，0] D．[0，2]
6．若函数
上最大值是最小值的3倍，则a=（ ）
A．
B．
C．
D．
7．函数
的最小正周期及最大值分别为ycy （ ）
A．
B．
C．
D．
8．双曲线
的两条渐近线夹角为 （ ）
A．
B．
C．
D．
9．
等于 （ ）
A．
B．
C．
D．
10．球面上有三点,其中任两点间球面距离等于大圆周长的
，经过这三点小圆周长为
，则球的体积为 （ ）
A．
B．
C．32
D．
11．已知
的值为 （ ）
A．
B．
C．
ycy D．或
12．在正方体ABCD—A1B1C1D1中，A1C1与AD1所成角为 （ ）
A．60° B．90° C．45° D．30°
二、填空题（每空4分，共16分）
13．已知
，集合
，则实数a的所有可能值的集合为
.
14．若等差数列
各项均为正，且
，则S12=
.
15．已知
的数量积为
.
16．椭圆
的半焦距为c，直线
与椭圆的一个交点横坐标为c，
则该椭圆离心率为 .
第II卷
三、解答题（共74分）
17．（本题12分）已知集合
，若满足关系
，求实数m的值和集合P.
18．（本题12分）甲、乙两人在罚球线投球命中概率分别为和
（1）甲、乙两人在罚球线各投球一次，求恰好命中一次的概率；
（2）甲、乙两人在罚球线各投两次，求这四次投球中至少命中一次的概率。
19．（本题12分）已知函数
在[0，2]上有最小值3，求a的值.
20．（本题12分）已知数列的前n项和Sn的是n的二次函数，且
.
（1）求Sn的表达式；
（2）求通项an.
21．（本题12分）已知函数
的图像经过点
（1）求函数的反函数；
（2）设
，求数列
的前n项和Sn.
22．（本题共14分）已知函数
的图像为曲线E
（1）若曲线E上存在点P使曲线E在P点处的切线与x轴平行，求a，b满足的关系式；
（2）若
时取极值，求
的值；
（3）在（2）的条件下，当
恒成立，求c的范围.
参考答案
一、选择题
BABBD ABBBB BA
二、填空题
13．
14． 48 15．±20 16．
三、解答题：
17．解：
18．解（1）记“甲投一次命中”为事件A，“乙投一次命中”为事件B，则
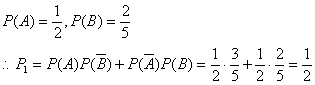
（2）甲、乙各投两次均不命中的概率
19．解：函数图像的对称轴为
分三种情况讨论
①当
（舍）
②当
（舍）
③
（舍）
综上可知
20．解：（1）设
则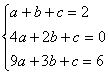
………………3分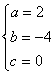 
（2）
21．解（1）由已知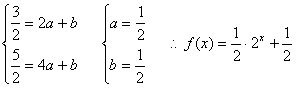
（2）
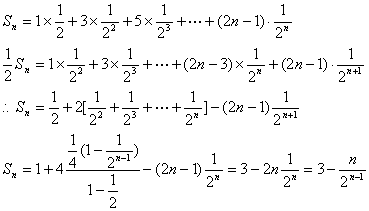
22．解（1）
即
（2）
的两根为
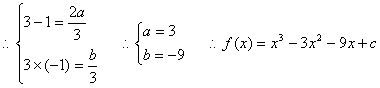
（3）在（2）的条件下
则
| x | －2 | （－2，－1） | －1 | （－1，3） | 3 | （3，6） | 6 |
| y′ | + | － | + | ||||
| y | c－2 | 递增 | 极大 | 递减 | 递增 | 极小 | C+54 |
故有
2．在等差数列
的值为 （ ）
A．24 B．22 C．20 D．－8
3．在各项均为正数的等比数列