 |
2005年高三年级第二次联考
数学试卷（理科）
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.
第Ⅰ卷（选择题，共60分）
注意事项：
1．请考生将自己的姓名、学号、班级填写在第Ⅱ卷的密封线内.
2．每小题选出答案后，请用铅笔在第Ⅱ卷前的答题栏内把对应题目的答案代号涂黑，不能答在试题卷上.
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．已知集合A={1，2，3，4}，B={5，6}，设映射
，使集合B中的元素在A中都有原象，这样的映射个数共有 （ ）
A．16 B．14 C．15 D．12
2．曲线
的一条切线平行于直线y=4x－1，则切点P0的坐标为 （ ）
A．（0，－2）或（1，0） B．（1，0）或（－1，－4）
C．（－1，－4）或（0，－2） D．（1，0）或（2，8）
3．已知函数
的值等于 （ ）
A．
B．
C．0 D．－2
4．已知相交直线l、m都在平面α内，并且都不在平面β内，若p：l、m中至少有一条与β相交；q：α与β相交，则p是q的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．不充分也不必要条件
5．若奇数
（ ）
A．0 B．1 C．
D．5
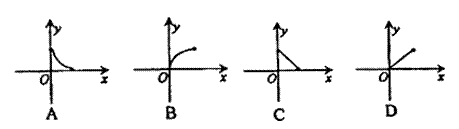6．一个棱锥被平行于底面的截面截成一个小棱锥和一个棱台（用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的部分叫棱台），若小棱锥的体积为y，棱台的体积为x，则y关于x的函数图象大致形状为 （ ）
7．若
，则实数a等于 （ ）
A．
B．
C．－ D．－
8．已知
顺次成等差数列，则 （ ）
A．y有最小值
，无最大值 B．y有最大值1，无最小值
C．y有最小值
，最大值1 D．y有最小值－1，最大值1
9．已知
p、q夹角为
如图所示，
若
，
，且D为BC中
点，则
的长度为（ ）
A．
B．
C．7 D．8
10．用6种不同的颜色把下图中A、B、C、D四块区域分开，
允许同一色涂不同的区域，但相邻的区域不能涂同一色，
则不同的涂法共有（ ）
A．400种 B．460种
C．480种 D．496种
11．若对于任意的
，函数
，则称在[a，b]上
可以替代
.若
，则下列函数中可以在[4，16]替代是（ ）
A．
B．
C．
D．
12．ABCD—A1B1C1D1是单位正方体，黑白两个蚂蚁从点A出发沿棱向前爬行，每走完一条棱称为“走完一段”.白蚂蚁爬地的路线是AA1→A1D1→……，黑蚂蚁爬行的路是AB→BB1→……，它们都遵循如下规则：所爬行的第
段所在直线必须是异面直线（其中i是自然数）.设白、黑蚂蚁都走完2005段后各停止在正方体的某个顶点处，这时黑、白两蚂蚁的距离是 （ ）
A．1 B．
C．
D．0
第Ⅱ卷（非选择题 共90分）
注意事项：
1．第Ⅱ卷共6页，用黑色签字笔直接答在试题上.
2．答卷前将密封线内的项目填写清楚.
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上.）
13．若
.
14．二次函数
的部分对应值如下表：
| x | －3 | －2 | －1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | －4 | －6 | －6 | －4 | 0 | 6 |
则不等式
的解是
.
15．购买手机的“全球通”卡，使用须付“基本月租费”（每月需交的固定费用）50元，在市内通话时每分钟另收话费0.40元；购买“神州行”卡，使用时不收“基本月租费”，但在市内通话时每分钟话费为0.60元，若某用户每月手机费预算为120元，则它购买
卡才合算.
16．设有四个条件：
①二直线平行的充要条件是它们的斜率相等；
②过点
相切的直线方程是
③平面内到两定点的距离之和等于常数的点的轨迹是椭圆；
④抛物线上任意一点M到焦点的距离都等于点M到其准线的距离.
其中正确命题的标号是 .
三、解答题（本大题共6小题，共74分，解答应写出文字说明、证明过程演算步骤）
17．（本小题满分12分）
若一个箱内装有分别标有号码1，2，…，50的50个小球，从中任意取出两个球把其上的号码相加，计算：
（1）其和能被3整除的概率；
（2）其和不能被3整除的概率.
18．（本小题满分12分）
设函数
的最大值为M，最小正周期为T.
（1）求M、T；
（2）若有10个互不相等的正数
且
，求：
的值.
19．（本小题满分12分）
如图，在多面体ABCDE中，AE⊥面ABC，BD//AE，且AC=AB=BC=BD=2，AE=1，F为CD中点.
（1）求证：EF⊥面BCD；
（2）求面CDE与面ABDE所成的二面角的余弦值.
20．（本小题满分12分）
一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比.
（1）将此枕木翻转90°（即宽度变为了厚度），枕木的安全负荷变大吗？为什么？
（2）现在一根横断面为半圆（半圆的半径为R）的枕木，用它来截取成长方形的枕木，其长度即为枕木规定的长度，问如何截取，可使安全负荷最大？
21．（本小题满分12分）
已知动点P与双曲线
的两个焦点F1、F2的距离之和为6.
（1）求动点P的轨迹C的方程；
（2）若
，求△PF1F2的面积
（3）若已知D（0，3），M、N在C上且
，求实数λ的取值范围.
22．（本小题满分14分）
已知在（－1，1）上有定义，
=1，且满足
对数列
（1）证明：在（－1，1）上为奇函数；
（2）求
的表达式；
（3）是否存在自然数m，使得对于任意
成立？若存在，求出m的最小值.
数学（理科）参考答案
1.B 2.B 3.C 4.C 5.C 6.C 7.B 8.A 9.A 10.C 11.C 12.B
13．
14．
15．神州行 16．④
17．解：因为基本事件总数
，从1到50中能被3整除的数有3，6，9等16个数，被3除余1的数有17个，被3除余2的数有17个，按题意：
（1）
…………7分
（2）
…………12分
18．解：
……2分
（1）M=2，
…………6分
（2）∵
∴
…………9分
又
∴
…………12分
|
∵AE⊥面ABC，BD//AE， ∴BD⊥面ABC，
又AG
面ABC，∴BD⊥AG，又AC=AB，
G是BC中点，∴AG⊥BC，∴AG⊥平面BCD，
∵F是CD的中点且BD=2，
∴FG//BD且FG=
BD=1，∴FG//AE. ……2分
又AE=1，∴AE=FG，故四边形AEFG是平行四边形，
从而EF//AG， ∴EF⊥面BCD. …………6分
（2）解：取AB的中点H，则H为C在面ABDE上的射影.过C作CK⊥DE于K，连接KH，由三垂线定理的逆定理得KH⊥DE，
∴∠HKC为二面角C—DE—B的平面角. …………8分
易知
由
可得CK=
在
中，
∴面CDE与面ABDE所成的二面角的余弦值为
. …………12分
20．解：（1）安全负荷
为正常数），翻转90°后，
.
∵
， ∴当
时，y1<y2，安全负荷变大；当
，安全负荷变小；当
，安全负荷不变. …………5分
（2）设截取的宽为a，高为d，则
∵枕木长度不变， ∴
最大时，安全负荷最大.
令
则
令
，舍去负）即取
，取
时，
u最大，即安全负荷最大. ………………12分
21．解：（1）已知C为椭圆，其中
，
∴b=2，∴C的方程为
…………3分
（2）由已知得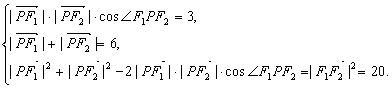
∴
∴
……7分
（3）设N（s，t），
，则由
，
可得
∴M、N在动点P的轨迹上，故
消去s可得
∴
故实数
的取值范围是
. ………………12分
22．解：（1）当x=y=0时，
；令x=0，得
∴对任意的
故在（－1，1）上为奇函数. …………3分
（2）∵
满足
∴
∵
在（－1，1）上为奇函数.
∴
；
由
……8分
（3）
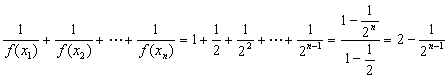
假设存在自然数m，使得对于任意
成立.
即
恒成立. ∴
解得
.
∴存在自然数，使得对于任意
成立.
此时，m的最小值为16. …………14分