湖北省实验中学2005—2006学年度高三测试
数 学
2005.12．23
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分，考试时间120分钟.
第I卷（选择题，共60分）
一、选择题（本大题共12小题，每小题5分，共60分.在每题给出的四个选项中，只有一项符合题意要求）.
1．集合
= （ ）
A．1 B．－1 C．0 D．不确定
2．（理）i+i2+…+i2004= （ ）
A．1 B．－1 C．0 D．以上均不正确
（文）已知：A={x－2≤x≤5}, B={xP+1≤x≤2P－1},若A∪B=A，则P的取值范围是（ ）
A．P<2 B．2≤P<3 C．P≤3 D．2≤P≤3
3．x+1－x－2>K恒成立，则K的取值范围是 （ ）
A．(－1,2) B．(－∞，－1) C．(－∞，－3) D．(－3，+∞)
4．关于x的不等式(mx－1)(x－2)>0,若此不等式的解集为：{x
<x<2},则m的取值范围是
（ ）
A．m>0 B．0<m<2 C．m>
D．m<0
5．y=f(x)有反函数，且y=f(x+2)的反函数为y=f－1(x－1),则f－1(1)－f－1(0)值为 （ ）
A．0 B．2 C．3 D．7
6．设A、B为两个命题，若B是┐A的必要但不充分条件，则┐B是A的（ ）条件
A．充分不必要 B．必要不充分
C．充要 D．不充分不必要
7．在等比数列{an}中，已知对任意正整数n，满足a1+a2+…+an=2n－1,则
=
（ ）
A．(2n－1)2 B．
(2n－1)2 C．4n－1 D．(4n－1)
8．y=2－sin(x+
)振幅与初相分别为 （ ）
A．－1， B．1， C．1，
D．－1，
9．给定下列命题：
（1）y=sinx在第一象限是增函数
（2）△ABC中三内角A、B、C成等差的充要条件是B=60°
（3）若cos(A－B)cos(B－C)cos(C－A)=1，则△ABC是正三角形
（4）函数y=Asin(wx+φ)的周期是T=
，其中正确命题的序号为 （ ）
A．①②③④ B．①④ C．②③ D．①②④
10．集合M={－2，0，1}，N={1，2，3，4，5}，映射f :M→N，使任意x∈M，都有x+f(x)+xf(x)是奇数，则这样的映射共有 （ ）
A．60个 B．45个 C．27个 D．11个
11．一元二次方程ax2+2x+1=0有一正根和一负根的充分不必要条件是 （ ）
A．a<0 B．a>0 C．a<－1 D．a>1
12．（理）函数y=1－x+sinx在（0，2π）上是 （ ）
A．单调增函数
B．单调减函数
C．（0，π）上是单调增函数，（π，2π）上是单调减函数
D．（0，π）上是单调减函数，（π，2π）上是单调增函数
（文）函数y=x4－2x2+5的单调减区间为 （ ）
A．
B．
C．[－1，1] D．
第Ⅱ卷（非选择题 共90分）
二、填空题（每题4分，共16分）
13．已知函数
=
.
14．已知函数f(x)=sinx+cosx , 则当x∈[－π，π]时f(x)的值域为 .
15．
的单调递增区间为
.
16．设f(x)表示－x+6和－2x2+4x+6中较小者，则f(x)的最大值为 .
三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤。
17．（本小题满分12分）
已知：sin(2α+β)=5sinβ,求tanα·cot(α+β)的值.
18．（本小题满分12分）
（理）若随机事件A在一次试验中发生的概率为P(0<P<1),用随机变量ξ表示A在一次试验中发生的次数。
（1）求Dξ的最大值.
（2）求
的最大值.
（文）求y=x4－2x2+5在[－2，2]上的最大值.
19．（本小题满分12分）
设f(x)是[－2，2]上的偶函数，且在[0，2]上是单调递减的，若f(1－m)<f(m),求m取值范围.
20．（本小题满分12分）
（理）计算：
（文）求函数y=cos6x+sin6x的周期.
21．（本小题满分12分）
是否存在一个等差数列，{an}使它的前n项和为Sn,且
是一个与n无关的常数，若存在，求出此常数，若不存在，说明理由.
22．（本小题满分14分）
定义域为R的函数f(x)满足：对于任意的实数x , y 都有f(x+y)=f(x)+f(y)成立，且当x>0时，f(x)<0恒成立.
（1）判断函数f(x)的奇偶性，并证明你的结论；
（2）证明f(x)为减函数；若函数f(x)在
上总有f(x)≤6成立，试确定f(1)应满足的条件；
（3）解关于x的不等式：
(n是一个给定的自然，a<0)
数学参考答案
一、选择题（5分×12=60分）：
1—6：ACCDBA 7—12：DCCBCB（文A）
二、填空题（4分×4=16分）：
13．f(x－1)=x2－2x－1(x≥3或x≤－1) 14．
15．
16．6
三、解答题（74分）
17．（12分）
18．（12分）（文）13
（理）ξ的分布列
| ξ | 0 | 1 |
| P | 1－P | P |
∴Eξ=P，Dξ=P－P2 ∴P=时，Dξ最大值为
（2）
的最大值为2－2
19．（12分）解：∵f(x)是偶函数，∴f(x)=f(x) ∴f(1－m)<f(m)
∵f(x)在[0,2]上是减函数，
1－m>m
∴ －2≤1－m≤2 解得：－1≤m<
－2≤m≤2
20．（12分）（文）T=
（理）（1）θ=
，原式=
（2）θ∈（0，），原式=3
（3）θ∈（，），原式=2 （4）θ=0，原式=3（5）θ=，原式=2
（θ=）
∴原式= 3（θ∈
）
2（θ∈
）
21．（12分）设存在{an}使=K（K为常数，则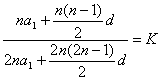
∴d(1－4K)－2(a1－d)(2K－1)=0,对n∈N*恒成立。
∴d(1－4K)=0
∴d=0时，K=
(2 a1－d) (2K－1)=0 d=2a1时，K=
22．（14分）（1）解：由已知可令x=y=0得f(0+0)=f(0)+f(0), ∴f(0)=0
∴对于任意x都有f(－x)= －f(x), ∴f(x)是奇函数.………………………………2分
（2）设x1, x2∈R，x1<x2, 则x2－x1>0，由已知f(x2－x1)<0
又f(x2－x1)=f(x2)+f(－x1)= f(x2)－f(x1) ∴f(x1)>f(x2)
∴f(x)在(－∞，+∞)上是减函数.……………………………………………4分
要使f(x)≤6恒成立，须f(－3)≤6
又f(－3)= －f(3)= －f(2+1)= －3f(1) ∴f(1)≥－2………………………8分
（3）
f(ax2)－f(x) >f(a2x)－f(a)
f(ax2)－f(a2x)>n[f(x)－f(a)]
f(ax2－a2x)>nf(x－a) f(ax2－a2x)>f[n(x－a)]
ax2－a2x<n(x－a)即(x－a)(ax－n)<0
∵a<0.
∴(x－a)(x－
)>0………………………………………………11分
讨论：1）当a<<0,即a<－
时原不等式解集为{xx>或x<a}.
2）当a=<0, 即a=－时原不等式解集为{xx≠－}.
3）当<a<0，即－<a<0时原不等式解集为{xx<或x>a}.……14分