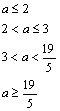华中师大一附中2005—2006学年度第一学期
高三年级第一次检测数学（文科）
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只
有一项是符合题目要求的。请把答案填在答题卡上。txjy
1．已知集合
，
，全集
，则
等于
A．[1，2] B．
,
,
C．
,
,
D．
,
,
2．若
，则
的值为txjy
A．
B．
C．
D．
3．设向量
，
，
，
，则
等于txjy
A．
，
B．
,
C．
D．
，
4．条件甲“
”是条件乙“
”的txjy
A．既不充分也不必要条件 B．充要条件
C．充分不必要条件 D．必要不充分条件
5．如果
，
，…，
为各项都不大于0的等差数列，公差
，则txjy
A．
B．
C．
D．
6．函数
，则
在
，
上是
A．单调递减函数且无最小值 B．单调递减函数且有最小值
C．单调递增函数且无最大值 D．单调递增函数且有最大值
7．函数
的图象关于
A．点
，0)对称 B．点
，0)对称
C．直线
对称
D．直线
对称
8．已知
是各项均为正数的等比数列，首项
，前三项和为21，则
A．33 B．72 C．84 D．189
9．若函数
在(0，2)上是增函数，函数
是偶函数，则
，
，
的大
小顺序是
A．
B．
C．
D．
10．
中，已知
，给出以下四个论断
①
②
③
④
其中正确的是
A．①③ B．②④ C．①④ D．②③
11．当
时，函数
的最小值为
A．2 B．
C．4 D．
12．不等式
对任意正整数
恒成立，则实数
的取值范围是
A．
B．
C．
D．
第Ⅱ卷（非选择题，共90分）
二、填空题：本大题共4小题，每小题4分，共16分。请把答案填在题中横线上。
13．函数
的反函数
__________。
14．中，
，
，，
，，则
的值是________。
15．等差数列中，
，
，若
，则
。
16．已知
，则函数
的最小值是___________。
三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。
17．（本小题满分12分）设有两个命题：
（1）关于
的不等式
的解集是
（2）函数
是减函数
若这两个命题都是真命题，求
的取值范围。
18．（本小题满分12分）若在，上是单调递增函数，解关于的不等式
19．（本小题满分12分）已知函数
（1）求函数的最小正周期；
（2）求函数的最大值与最小值；
（3）写出函数的单调递增区间。
20．（本小题满分12分）已知等差数列的前11项和为220
（1）数列中是否存在某一项的值为常数，若存在，请求出该项，若不存在，请说明理由；
（2）若中
，设
，求数列
前项的积；
（3）若从数列中依次取出第3项，第9项，第27项，…，第
项，按从小到大的顺序组成一个新的数列
，求数列的前项和
。
21．（本小题满分12分）将二次函数
的图象按
，平移，使得平移后的图象与
函数
的图象有两个不同的公共点
、
，且向量
为原点)与向量，共线，求平移后的图象的解析式。
22．（本小题满分14分）已知函数
的图象过点(1，1)，函数
的图象关于
直线
对称，且
时
，若
（1）求函数的解析式；
（2）求函数在区间[2，3]上的最小值。
高三年级数学（文）期中参考答案
一、1-5 D B B B B A 5-10 B C D B C C
二、13．
14．
15．669
16．1
三、17．由（1）真知
即
由（2）真知 
所以的取值范围是，
18．原不等式可变为 
即
当
时，原不等式解集为
或
当
时，原不等式解集为
当
时，原不等式解集为
或
19．
（1）
的最小正周期为
（2）的最大值为2，最小值为
（3）的单调递增区间为
，
20．（1）设等差数列
公差为
即
数列中存在确定的项第六项且
（2）若
前项的积
而
（3）由（1）知，
数列
为
，
，…，
21．设所求解析式为
由 
得
设
，
，
，
则
则
又
，
，
依题意
所求解析式为
22．（1）
的图象关于直线对称，且
时
又
（2）由（1）知
当
时在[2，3]上，
[2，3]
显然有[2，3]时 
在[2，3]上单调递增
当
时，在[2，3]上不小于0且
当
时，在[2，3]上
若
，在
，
单调递增，在
，
单调递减
或
令
即
时，
时，
若
时，在[2，3]上恒大于0
