江苏省泰兴中学2006届一模适应性考试
高三数学
2006.3.12
一、选择题：本大题共12小题，每小题5分，共60分.
1．cos600°= （ ）
A．
B．
C．
D．
2．已知函数
= （ ）
A．b B．－b C．
D．－
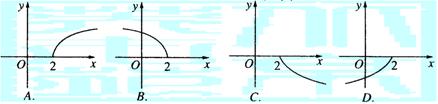
3．函数
的反函数的图象大致是 （ ）
|
4．一元二次方程
有一个正实数根和一个负实数根的充分不必要条件
是 （ ）
A．
B．
C．
D．
5．一所中学有高一、高二、高三学生共1600名，其中高三学生400名.如果通过分层抽样的方法从全体高中学生中抽取一个160人的样本，那么应当从高三年级的学生中抽取的人数是 （ ）
A．20 B．40 C．60 D．80
6．已知平面
、
都垂直于平面
，且
给出下列四个命题：
①若
；②若
；③若
；④若
.
其中真命题的个数为 （ ）
A．4 B．3 C．2 D．1
7．若把函数
的图象按向量
平移后，得到函数
的图象，则原图象的函数解析式可以为 （ ）
A．
B．
C．
D．
8．已知奇函数
的定义域为
，且对任意正实数
，恒有
，则一定有 （ ）
A．
B．
C．
D．
9．已知平面上直线l的方向向量e=
，点O（0，0）和A（1，－2）在l上的射影分别是O1和A1，则
，其中λ= （ ）
A．
B．－ C．2 D． －2
10．若双曲线
和椭圆
的离心率互为倒数，那么以a，b，m为边长的三角形是 （ ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．等腰三角形
11．若正四面体的四个顶点都在一个球面上，且正四面体的高为4，则该球的体积为（ ）
A．
B．18
C．36 D．
12．设集合
，则A所表示的平面区域(不含边界的阴影部分)是 ( )
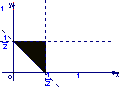
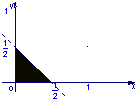
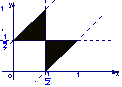
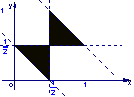
A． B． C． D．
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中的横线上.
13．
的展开式中常数项等于
.
14．以正方体ABCD—A1B1C1D1的8个顶点中4个为顶点，且4个面均为直角三角形的四面体是 （只要写出一个四面体即可）.
15．若双曲线
的焦点到相应准线的距离是2，则k= .
16．若含有集合A={1，2，4，8，16}中三个元素的A的所有子集依次记为B1，B2，B3，…，Bn（其中n∈N*），又将集合Bi（i=1，2，3，…，n）的元素的和记为
，则
=
.
17．正方体AC1中，S，T分别是棱AA1，A1B1上的点，如果
那么
18．若直线
与圆
没有公共点，则以
为点
的坐标，过点的一条直线与椭圆
的公共点有
个
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
19．（本小题满分12分）
在任何两边都不相等的锐角三角形ABC中，已知角A、B、C的对边分别为a、b、c，且
（Ⅰ）求角B的取值范围；（Ⅱ）求函数
的值域；（Ⅲ）求证：
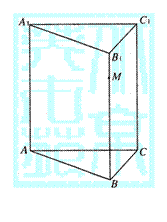
20．（本小题满分12分）
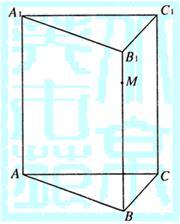
如图，已知正三棱柱ABC—A1B1C1的底面边长为1，点M在侧棱BB1上.
（Ⅰ）若BM=
，求异面直线AM与BC所成的角；
（Ⅱ）当棱柱的高BB1等于多少时，AB1⊥BC1？请写出你的证明过程.
21．（本小题满分12分）
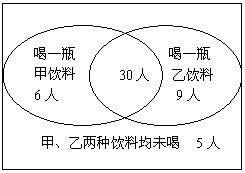
高三（1）班50名学生在元旦联欢时，仅买了甲、乙两种瓶装饮料可供饮用.在联欢会上甲饮料喝掉了36瓶，乙饮料喝掉了39瓶.假设每个人至多喝1瓶甲饮料和1瓶乙饮料，并且有5名学生两种饮料都没有喝，随机选取该班的1名学生，计算下列事件的概率；
（Ⅰ）他没有喝甲饮料；（Ⅱ）他喝了1瓶乙饮料但是没有喝甲饮料；
（Ⅲ）他喝了1瓶甲饮料和1瓶乙饮料.
22．（本小题满分14分）
直角坐标平面内，△ABC的两上顶点A、B的坐标分别为A（－1，0）、B（1，0），平面内两点G、M同时满足以下条件：
①
；②
；③
（Ⅰ）求△ABC的顶点C的轨迹方程；（Ⅱ）过点P（2，0）的直线l与△ABC的顶点C的轨迹交于E、F两点，求
的取值范围.
23．（本小题满分12分）
已知
是定义在实数集R上的函数，其图象与x轴相交于A，B，C三点，若B点坐标为（2，0），且在[－1，0]和[4，5]上有相同的单调性，在[0，2]和[4，5]上有相反的单调性.
（Ⅰ）求c的值，写出极值点横坐标的取值范围（不需要证明）；
（Ⅱ）在函数的图象上是否存在一点M（
），使曲线
在点M处的切线斜率为3b？若存在，求出点M的坐标；若不存在，说明理由.
江苏省泰兴中学2006届一模适应性考试
高三数学
参考答案及评分标准
一、选择题：本大题共12小题，每小题5分，共60分.
1.A 2.B 3.C 4.C 5.B 6.A 7.A 8.D 9.D 10.B 11.C 12.A
二、填空题：本大题共4小题，每小题4分，共16分.
13．14 14．四面体A1ABC（不唯一） 15．6 16．186 17．
18．2
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
19．解：（Ⅰ）∵
∴
…………2分
∴
∴
…………4分
（Ⅱ）∵
…………5分
由（Ⅰ）得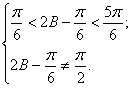
…………6分
∴
，∴函数的值域为（
）.……8分
（Ⅲ）∵
∴
…………9分
，∵
∴
…………11分 ∴ …………12分
20．解：（Ⅰ）在正三棱柱ABC—A1B1C1中，B1B⊥底面ABC，
|
.……2分
∴
,……4分
又∵
∴
…………5分
异面直线AM与BC所成的角为
……6分
（Ⅱ）∵
…8分令
，
∴当
时，AB1⊥BC1.…………12分
21．解：（Ⅰ）用A表示事件“他喝了1瓶甲饮料”，则
就表示事件“他没有喝甲饮料”.
因此，选取的人没喝甲饮料的概率
…………4分
（Ⅱ）用B表示事件“他喝了1瓶乙饮料但是没有喝甲饮料”，
C表示事件“他两种饮料都没有喝”，则B和C互斥，并且B+C=. …………6分
由P（）=P（B+C）=P（B）+P（C），
得P（B）=P（）－P（C）=
……8分
（Ⅲ）用D表示事件“他喝了1瓶甲饮料和1瓶乙饮料”，
E表示事件“他喝了1瓶饮料”，则D和B互斥，并且E=D+B. …………10分
由P（E）=P（D+B）=P（D）+P（B），得P（D）=P（E）－P（B）=
或设喝了一瓶甲饮料和一瓶乙饮料的人数为x，
则
∴
出如下韦恩图. …………3分
（Ⅰ）他没有喝甲饮料的概率为
…………6分
（Ⅱ）他喝了1瓶乙饮料但是没有喝甲饮料的概率为
…………9分
（Ⅲ）他喝了1瓶甲饮料和1瓶乙饮料的概率为
…………12分
22．解：（Ⅰ）设点C，G的坐标分别为
，
0
， …………2分
由
，知点M的坐标为（0，y0）， ……3分
由
，可得
∴
点C的轨迹方程是
…………6分
（Ⅱ）直线l的斜率为k（k≠0），则它的方程为y=k（x－2），
由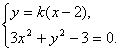
可得
…………8分
其中
∴
…………9分
设两交点E、F的坐标分别为 
，
由韦达定理得：
又因为
从而
……11分
又
∴的取值范围是（3，
）. …………14分
23、解：（Ⅰ）∵在[－1，0]与[0，2]上有相反的单调性，
∴
…………2分
极值点横坐标的取值范围
…………4分
（Ⅱ）令
∴函数的极值点为
…………6分
根据（Ⅰ）得，
∴
………8分
假设存在满足条件的点M
，
令
……（1）
∴方程（1）没有实数根.
∴不存在满足条件的M点. …………12分