惠州一中2007届数列单元检测
（时间：100分钟，满分：100分）
一、选择题（本大题共8小题，每小题5分，满分40分）
1．在等差数列
中，已知前20项之和
，则
( )
A． 34 B． 51 C． 68 D． 70
2．在等差数列中，
，
，则
( )
A． 30 B． 32 C． 34 D． 36
3．若数列满足
，则此数列是（ ）
A． 等差数列 B． 等比数列
C． 既是等差数列又是等比数列 D． 既非等差数列又非等比数列
4．在等差数列中，
，若
，则
的最小值为（ ）
A． 60 B． 62 C． 70 D． 72
5．已知为等比数列，对于任意
，有
，则
（ ）
A．
B．
C． 
D． 
6．已知递增数列的通项为
，则实数
满足（ ）
A． 
B． 
C． 
或
D． 
7．已知方程
的四根组成首项为
的等差数列，则
（
）
A． 
B．
C．
D． 
8．若等比数列满足
，公比
，则
的值是 （ ）
A． B． 
C．
D． 
二、填空题（本大题共6小题，每小题5分，满分30分）
9．在数列中，已知
且
，则
_____________．
10．正项等差数列中，
则
_________．
11．在等比数列中，
，已知
，则公比
__________．
12．在等比数列中，
，
，则
_________．
13．
等于_________．
14． 已知数列中，
，则
的值是_________．
三、解答题(本大题共6小题，满分80分)
15.（满分14分）设是一个公差为
的等差数列，它的前10项和
且
，
，
成等比数列。（1）证明
；（2）求公差
的值和数列的通项公式.
16. （满分14分）若S
是公差不为0的等差数列
的前n项和，且
成等比数列。
(Ⅰ)求数列的公比； (Ⅱ)若
，求的通项公式。
17．（满分12分）已知数列中，
，且
，求
及
．
18．（满分12分）数列满足
，求的前项和．
19．（满分14分）已知等差数列中，
，
(1) 求数列的通项公式；
(2) 若从数列中依次取出第2项，第4项，第8项
,第
项，按原来的顺序组成一个新数列
，求
20．（满分14分）已知数列中，
，
，其中，
为常数且为正整数，为负整数．
(1) 求通项；(2) 若
，求，；(3) 对于(2)中的，值，求此数列所有负项的和．
答案
一、 1.A 2.B 3.A 4.B 5.C 6.C 7C 8.A
二、9.
10. 28 11.
3 12. 105 13. 
14.
三、15.（1）证明：因，，成等比数列，故
，而是等差数列，有
，
,于是 
，即
，化简得
（2）解：由条件和
，得到
，由（1），，代入上式得
，故 
，
，
16.解：（Ⅰ）设数列的公差为,由题意，得 
所以
因为
，所以 
故公比
（Ⅱ）因为
所以
因此
17.
，
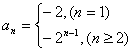16.
18．
19. (1)
(2)
.
20. (1)
，
(2)
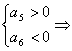
所以
, 当
时,
,所以
．当
时，不是负整数．所以
(3)