江都市仙城中学高三年级月考
数学试卷
参考公式:
三角函数的和差化积公式
![]()
![]()
![]()
![]()
若事件A在一次试验中发生的概率是P,则它在n次独立重复试验中恰好发生k次的概率
![]()
一组数据![]() 的方差
的方差
![]() +
+![]() +…+
+…+![]() ]
]
其中![]() 为这组数据的平均数
为这组数据的平均数
一、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1.设![]() ={(
={(![]() )
)![]() =3},
=3},![]() ={(
={(![]() )
)![]() =1},满足C
=1},满足C![]() A∩B的集合
A∩B的集合![]() 的个数是
的个数是
A.0 B.1 C.2 D.4
2.抛物线![]() 的焦点坐标是
的焦点坐标是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.设等比数列![]() 的前n项和为Sn,若
的前n项和为Sn,若![]() ,则
,则![]() txjy
txjy
A.1:2 B.2:3 C.3:4 D.1:3
4.若P: ![]() ,Q:
,Q: ![]() ,则P 是Q的
,则P 是Q的
A.充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D.即不充分也不必要条件
5.函数![]() 的图象相邻的两条对称轴之间的距离是
的图象相邻的两条对称轴之间的距离是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
6.下列命题中正确的是
A.若直线![]() ∥平面M,则直线
∥平面M,则直线![]() 的垂线必平行于平面M;
的垂线必平行于平面M;
B.若直线![]() 与平面M相交,则有且只有一个平面经过
与平面M相交,则有且只有一个平面经过![]() 且与平面M垂直;
且与平面M垂直;
C.若直线![]() 平面M,
平面M,![]() 相交,且直线
相交,且直线![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,则
,则![]() ⊥M;
⊥M;
D.若直线![]() ∥平面M,直线
∥平面M,直线![]() ⊥
⊥![]() ,则
,则![]() ⊥M.
⊥M.
7.已知![]() 展开式中常数项为1120,其中实数
展开式中常数项为1120,其中实数![]() 是常数,则展开式中各项系数的和为
是常数,则展开式中各项系数的和为
A.![]() B.1或
B.1或![]() C.
C. ![]() D.1或
D.1或![]()
8.已知函数![]() 是偶函数,则一定是函数
是偶函数,则一定是函数![]() 图象的对称轴的直线是
图象的对称轴的直线是
A. ![]() B.
B.![]() C.
C. ![]() D.
D.![]()
9.如图,正方形![]() 的顶点
的顶点![]() ,
,![]() ,顶点
,顶点![]() 位于第一象限,直线
位于第一象限,直线![]() 将正方形
将正方形![]() 分成两部分,记位于直线
分成两部分,记位于直线![]() 左侧阴影部分的面积为
左侧阴影部分的面积为![]() ,则函数
,则函数![]() 的图象大致是
的图象大致是
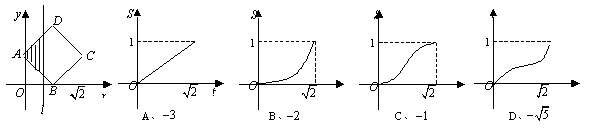
10.已知直线l:Ax+By+C=0(A、B不全为0)及两点P1(x1,y1),P2(x2,y2),若(Ax1+By1+C)(Ax2+By2+C)>0,且Ax1+By1+C> Ax2+By2+C,则
A.直线l与直线P1P2不相交 B. 直线l与线段P2 P1的延长线相交
C.直线l与线段P1 P2的延长线相交 D. 直线l与线段P1P2相交
11.已知等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,且
,且![]() ,
,![]() ,则过点
,则过点![]() 和
和![]() 的直线的一个方向向量的坐标是
的直线的一个方向向量的坐标是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12.已知A、B、C三点共线,O是这条直线外一点,设![]()
![]()
![]() 且存在实数m,使
且存在实数m,使![]() 0成立,则点A分
0成立,则点A分![]() 的比为
的比为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题:本大题共6小题,每小题4分,满分24分。
13.某校有教师200人,男学生1200人,女学生1000人,现用分层抽样的方法从所有师生中抽取一个容量为n的样本,已知从女学生中抽取的人数为80人,则n的值为_______
14.已知![]() ,则
,则![]() 的值为_____________
的值为_____________
15.已知函数![]() =则
=则![]() .
.
16.在△ABC中,a、b、c分别是∠A、∠B、∠C所对的边。若∠B =![]() ,b=2
,b=2![]() ,c=2,则∠A=
.
,c=2,则∠A=
.
17.已知椭圆![]() 与双曲线
与双曲线![]() 在第一象限内的交点为
在第一象限内的交点为![]() ,则点
,则点![]() 到椭圆右焦点的距离等于______
到椭圆右焦点的距离等于______
18.若函数![]() 的图象与直线
的图象与直线![]() 有且仅有四个不同的交点,则
有且仅有四个不同的交点,则![]() 的取值范围是__________
的取值范围是__________
三、本大题共5小题,共66分。解答应写出文字说明、证明过程或演算步骤。
(19)(本小题满分12分,每小问满分4分)
已知某地区人口数量较大,经检测有5%的男人、1%的女人是色盲,假设该地区男女各占一半。
(1)随机挑选一人,求此人恰是色盲的概率;
(2)随机挑选三人,恰有两人恰是色盲的概率。
(3)该地区有一所中学,男生200人、女生100人,现从中任意抽取男生、女生各5名进行体检,发现色盲的概率有多大?(用算式表示即可)。
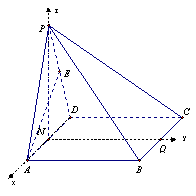
17.(本题满分14分)如图,四棱锥P -ABCD的底面是矩形,侧面PAD是
正三角形,且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
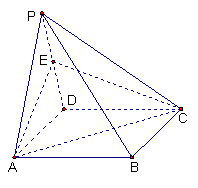 (1)求证:直线PB与平面EAC的关系;
(1)求证:直线PB与平面EAC的关系;
(2)求证:AE⊥平面PCD;
(3)若AD = AB,试求二面角A-PC-D的正切值;
(4)当![]() 为何值时,PB⊥AC ?
为何值时,PB⊥AC ?
(21) (本小题满分14分,第一小问满分6分,第二小问满分8分)
已知函数![]()
(Ⅰ)若函数![]() 在区间(-∞,+∞)上为单调函数,求实数a的取值范围;
在区间(-∞,+∞)上为单调函数,求实数a的取值范围;
(Ⅱ)设A(x1,
![]() )、B(x2,
)、B(x2, ![]() )是函数
)是函数![]() 的两个极值点,若直线AB的斜率不小于
的两个极值点,若直线AB的斜率不小于![]() ,求实数a的取值范围。
,求实数a的取值范围。
19.(本小题满分14分)
已知函数![]() ,
,
(1)若函数![]() 的图象在点
的图象在点![]() 处的切线与直线
处的切线与直线![]() 平行,函数
平行,函数![]() 在
在![]() 处取得极值,求函数
处取得极值,求函数![]() 的解析式,并确定函数的单调递减区间;
的解析式,并确定函数的单调递减区间;
(2)若![]() ,且函数
,且函数![]() 在
在![]() 上是减函数,求
上是减函数,求![]() 的取值范围。(浙理)
的取值范围。(浙理)
22.(本题满分14分)已知点A(-2,0)、B(2,0),动点C在x轴上的射影为点D,且满足![]()
(1)求动点C的轨迹E的方程;
(2)若P、Q为轨迹E上的不同两点,且满足PA⊥QA ,试问直线PQ是否恒过一个定点?若是,则求出该定点坐标;若不是,请说明理由。
23.(本题满分14分)已知曲线![]() ,过
,过![]() 上的点
上的点![]() 作曲线
作曲线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,再过点
,再过点![]() 作
作![]() 轴的平行线交曲线
轴的平行线交曲线![]() 于点
于点![]() ,再过点
,再过点![]() 作曲线
作曲线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,再过点
,再过点![]() 作
作![]() 轴的平行线交曲线
轴的平行线交曲线![]() 于点
于点![]() ,……,依次作下去,记点
,……,依次作下去,记点![]() 的横坐标为
的横坐标为![]()
![]()
(1)求数列![]() 的通项公式;(2)设数列
的通项公式;(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]()
(3)求证:![]()
参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | C | A | C | C | B | A | C | C | B | A |
二、填空题
13、188 14、![]() 15、
15、![]() 16、
16、![]() 或
或![]() 17、8 18、[1,
17、8 18、[1,![]()
三、解答题
19.(1)0.03 (2)0.002619 (3)1-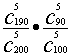
20. 解:(1)PB//平面EAC。 2分;(2)
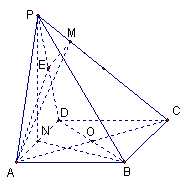

正三角形PAD中,E为PD的中点,所以,![]() ,
,
又![]() ,所以,AE⊥平面PCD。 6分
,所以,AE⊥平面PCD。 6分
(3)在PC上取点M使得![]() 。
。
由于正三角形PAD及矩形ABCD,且AD=AB,所以![]()
连接![]() ,因为AE⊥平面PCD,所以,
,因为AE⊥平面PCD,所以,![]() 。
。
所以,![]() 为二面角A-PC-D的平面角。
为二面角A-PC-D的平面角。
在![]() 中,
中,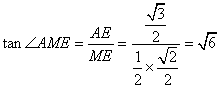 。
。
即二面角A-PC-D的正切值为![]() 。 10分
。 10分
(4)设N为AD中点,连接PN,则![]() 。
。
又面PAD⊥底面ABCD,所以,PN⊥底面ABCD。
所以,NB为PB在面ABCD上的射影。
要使PB⊥AC,需且只需NB⊥AC
在矩形ABCD中,设AD=1,AB=x
则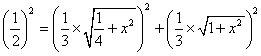 ,
,
 解之得:
解之得:![]() 。
。
所以,当![]()
![]() 时,PB⊥AC。 14分
时,PB⊥AC。 14分
证法二:(按解法一相应步骤给分)
设N为AD中点,Q为BC中点,则因为![]() PAD是正三角形,底面ABCD是矩形,所以,
PAD是正三角形,底面ABCD是矩形,所以,![]() ,
,![]() ,又因为侧面PAD⊥底面ABCD,所以,
,又因为侧面PAD⊥底面ABCD,所以,![]() ,
,![]() ,
,
以N为坐标原点,NA、NQ、NP所在直线分别为![]() 轴如图建立空间直角坐标系。设
轴如图建立空间直角坐标系。设![]() ,
,![]() ,则
,则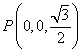 ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,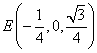 。
。
(2)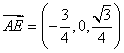 ,
,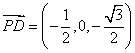 ,
,![]() ,
,
![]() ,
,![]()
所以,![]() 。
。
又![]() ,
,![]() ,所以,AE⊥平面PCD。 6分
,所以,AE⊥平面PCD。 6分
(3)当![]() 时,由(2)可知:
时,由(2)可知: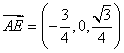 是平面PDC的法向量;
是平面PDC的法向量;
设平面PAC的法向量为![]() ,则
,则![]() ,
,![]() ,即
,即
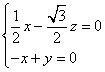 ,取
,取![]() ,可得:
,可得:![]() 。所以,
。所以,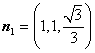 。
。
向量![]() 与
与![]() 所成角
所成角![]() 的余弦值为:
的余弦值为: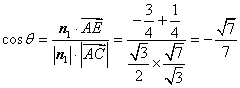 。
。
所以,tan q = 。
又由图可知,二面角A-PC-D的平面角为锐角,所以,二面角A-PC-D的平面角就是向量![]() 与
与![]() 所成角
所成角![]() 的补角。其正切值等于
的补角。其正切值等于![]() 。 10分
。 10分
(4)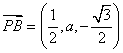 ,
,![]() ,令
,令![]() ,得
,得![]() ,所以,
,所以,![]() 。所以,当
。所以,当![]()
![]() 时,PB⊥AC。 14分
时,PB⊥AC。 14分
21. (Ⅰ)因为函数![]() 在(-∞,+∞)上为单调递增函数,
在(-∞,+∞)上为单调递增函数,
所以![]() 在(-∞,+∞)上恒成立。
在(-∞,+∞)上恒成立。
由△=![]() ,解得0<a<4 …………………………………………4分
,解得0<a<4 …………………………………………4分
又当a=0时,![]() (-∞,+∞)上为单调递增函数,
(-∞,+∞)上为单调递增函数,
又当a=4时,![]() 在(-∞,+∞)上为单调递增函数,所以0≤a≤4
…………………………………………6分
在(-∞,+∞)上为单调递增函数,所以0≤a≤4
…………………………………………6分
(Ⅱ)依题意,方程![]() =0有两个不同的实数根x1,、x2,
=0有两个不同的实数根x1,、x2,
由△=![]() ,解得a<0,或a>4,且x1+x2=-a,x1x2= a …………………8分
,解得a<0,或a>4,且x1+x2=-a,x1x2= a …………………8分
所以![]()
![]() ,
,
所以![]()
![]()
=![]() . ………………………………12分
. ………………………………12分
解之得-1≤a≤5, 所以实数a的取值范围是-1≤a<0,或4<a≤5. ……………14分
22.
23. 解(1)![]() 曲线
曲线![]() 在点
在点![]() 处的切线
处的切线![]() 的斜率是
的斜率是![]() ,
,![]() 切线
切线![]() 的方程是
的方程是![]() ,由于点
,由于点![]() 的横坐标等于点
的横坐标等于点![]() 的横坐标
的横坐标![]() ,所以,令
,所以,令![]() ,
,
得![]() ,
,![]() 数列
数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,
的等比数列,![]()
(2)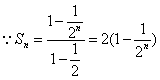 ,
,![]() ,令
,令![]() ,则
,则![]()
![]()
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 有最大值1,即
有最大值1,即![]()
(3)![]() ,
,![]() ,即
,即![]() ,
,
![]() 数列
数列![]() 是首项为1,公比为4的等比数列
是首项为1,公比为4的等比数列
![]()