江西省高安中学2005-2006学年度高三期末试题
数 学 试 卷
2006.1
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)共两部分.
第Ⅰ卷(选择题,共60分)
一、选择题(单项选择,5分×12=60分)
1.已知数列{![]() }是等差数列,且
}是等差数列,且![]() ,则
,则![]() 等于 ( )
等于 ( )
A.3 B.4 C.5 D.6
2.已知函数![]() ,则
,则![]() 的最小正周期等于 ( )
的最小正周期等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2![]()
3.已知数列{![]() }的通项公式为
}的通项公式为![]() ,则前2005项和S2005等于 ( )
,则前2005项和S2005等于 ( )
A.1 B.-1 C.0 D.2005
4.已知x、y是正实数,且x、a1,a2,y成等差数列,x、b1,b2,y成等比数列,则![]()
的取值范围是 ( )
A.R B.![]() C.
C.![]() D.
D.![]()
![]()
5.已知等比数列{![]() }的首项为1,公比为q,前n项和是S,由原数列各项的倒数组成一个
}的首项为1,公比为q,前n项和是S,由原数列各项的倒数组成一个
新数列{![]() },则{
},则{![]() }的前n项和是 ( )
}的前n项和是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.等差数列{![]() }中,已知
}中,已知![]() ,则使它前n项和Sn取得最大值的正整数n是
,则使它前n项和Sn取得最大值的正整数n是
( )
A.4或5 B.5或6 C.6或7 D.不存在
7.已知![]() 是方程
是方程![]() 的两个根,且
的两个根,且![]()
则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.-
D.-![]() 或
或![]()
8.已知![]() =2006,则
=2006,则![]() 值为 ( )
值为 ( )
A.2004 YCY B.2005 C.2006 D.2007
9.设函数![]() 若当
若当![]() 时,
时,![]() 恒成立,
恒成立,
则实数m的取值范围是 ( )
A.(0,1) B.(-∞,0) C.(-∞,![]() ) D.(-∞,1)
) D.(-∞,1)
10.设![]() ,曲线
,曲线![]() 在点P(
在点P(![]() 处切线的倾斜角的
处切线的倾斜角的
取值范围是[0,![]() ],则点P到曲线
],则点P到曲线![]() 对称轴的距离的取值范围是 ( )
对称轴的距离的取值范围是 ( )
A.![]() ] B.
] B.![]() ] C.
] C.![]() ] D.
] D.![]() ]
]
11.正方体的6个面中任取3个面,其中有2个面不相邻的概率为 ( )
|
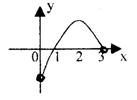
12.已知![]() 是定义在(-3,3)上的奇函数,当
是定义在(-3,3)上的奇函数,当![]() 时,
时,![]()
的图象如右所示,那么不等式![]() 的解集为( )
的解集为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共90分)
二、填空题(每题4分,共16分)
13.数列满足条件:(1)任意连续二项的和大于零;(2)任意连续三项的和小于零则这样的数列最多有 项.
14.设集合M={-1,0,1},N={2,3,4,5,6,},映射f:M→N,使对任意的![]() 都
都
有![]() 是奇数,这样的映射有
个.
是奇数,这样的映射有
个.
15.函数![]() 在区间
在区间![]() )上是增函数,则a的取值范围为
)上是增函数,则a的取值范围为
.
16.已知数列{![]() }满足
}满足![]() ,则数列{
,则数列{![]() }的通项公式
}的通项公式
![]() =
.
=
.
三、解答题:(解答应写出文字说明,证明过程或演算步骤,共6个小题,共74分)
17.(12分)ycy
从1,2,3,4,5,6这6个数中任取2个不同的数作差,
(文)(1)记事件A=“差的绝对值等于1”,求P(A);
(2)记事件B=“差的绝对值不小于3”,求P(B).
(理)设差的绝对值为ξ,求ξ的分布列及数学期望.
18.(12分) 已知![]() 求
求![]() 的值.
的值.
19.(12分) 已知![]() 内有相异的两解
内有相异的两解![]() ,求实数
,求实数![]() 的取值范围,以及
的取值范围,以及![]() 的值.
的值.
20.(12分) 设![]() 和
和![]() 分别是等差数列和等比数列,且
分别是等差数列和等比数列,且![]() ,试比较
,试比较![]() 的大小.
的大小.
21.(12分) 设数列![]() 的前n项和为
的前n项和为![]() 为等比数列,且
为等比数列,且![]() ,
,![]()
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前n项和Tn.
的前n项和Tn.
22.(14分) (理)已知数列![]() 中,
中,![]()
(1)求证:![]() ;(2)求证:
;(2)求证:![]() 为递增数列;(3)求证:
为递增数列;(3)求证:![]()
(文)设![]() ,点P(t,0)是函数
,点P(t,0)是函数![]() 的图象的一个
的图象的一个
公共点,两函数的图象在P点处有相同的切线,
(1)用t表示a、b、c;
(2)若函数![]() 在(-1,3)上单调递减,求t的取值范围.
在(-1,3)上单调递减,求t的取值范围.
参考答案
一、选择题:(5分×12=60分)
1.C 2.B 3.A 4.C 5.C 6.B 7.B 8.C 9.D 10.B 11.C 12.B
二、填空题:(共16分,每题4分)
13.3 14.50 15.[2-2![]() ,2] 16.
,2] 16.![]()
三、解答题:(共74分)
17.(12分)(理)
| ξ | 1 | 2 | 3 | 4 | 5 |
| P |
|
|
|
|
|
Eξ=![]() (文) P(A)=
(文) P(A)=![]() ,P(B)=
,P(B)=![]()
18.(12分)解得:![]()
19.(12分)解:![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
20.(12分)解:(1)当![]() 时,则
时,则![]() ;
;
(2)当![]() 时,则
时,则![]() ;
;
(3)当![]() 时,则
时,则![]() ; 综上:
; 综上:![]() .
.
21.(12分)解:(1)![]()
(2)![]()
22.(14分)解:(理)(1)、(2)用数学归纳法证明. (3)用放缩法证明.
(文)(1)![]()
(2)![]() .
.