热点题型猜测
1.已知数列
是首项为
，公差为
的等差数列，若数列
是等比数列，则其公比为: 
2.已知双曲线
的右焦点为
，右准线为
，一直线交双曲线的两支于
两点，交于
点．则
A. 
B.
C.
D.
的大小不确定
3.已知点P是椭圆
上的动点，F1、F2为椭圆的两个焦点，O为坐标原点，若M是
的角平分线上一点，
，则
取值范围是
A.
B.
C.
D.
4.设非零向量,,,若= + + ,则的取值范围
A．[0,1] [0,2] [0,3] [-3,3]
5.已知不等式
的解集为
，则有
A.
B.
C.
D.
6.设
、
是方程
的两个不相等的实数根，那么过点
和点
的直线与圆
的位置关系是
A.相交 B.相切 C.相离 D.随
的值变化而变化
7.定义在区间[2，4]上的函数
是常数）的图象过点（2，1），
则函数
的值域为
A.[2，5] B.
C.[2，10] D.[2，13]
8.已知F1,F2分别为双曲线
的左右焦点,P为双曲线左支上任意一点,若
最小值是8
,则双曲线离心率e的取值范围是
A.
B.
C.
D.
9.已知二次函数f（x）＝ax2＋bx＋c的图象如图所示，若M＝｜a－b＋c｜＋｜2a＋b｜，N＝｜a＋b＋c｜＋｜2a－b｜，则M与N的大小关系是
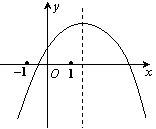A
M≥N B M≤N
C M＜N D M＞N
10.函数
的定义域为______________.
11.已知对称中心为原点的双曲线与椭圆
有公共的焦点，且它们的离心率互为倒数，则该双曲线的方程为 __
_______ ．
12.已知函数
,当
时,
恒成立,则实数
的取值范围是___________.
13.类比椭圆性质的研究，试写出一个关于曲线
的性质：
14.已知空间三个平面
两两垂直，直线与平面
所成的角都是
，则直线与平面
所成角的余弦值是_________.
15.将矩形
绕
边旋转
得矩形
,再将绕边
旋转得
得
, ,求面与面所成的锐二面角.
新 题:
1.某楼梯共有n级台阶，每步只能跨上1级或2级台阶，走完该楼梯n级台阶共有
种不同的走法，则
=
2.给出下列四个命题：①有两个面平行，其余各面都是平行四边形的几何体是棱柱；②有两侧面与底面垂直的棱柱是直棱柱；③过斜棱柱的侧棱作棱柱的截面，所得图形不可能是矩形；④所有侧面都是全等的矩形的四棱柱一定是正四棱柱。其中正确的命题的个数为（ ）个
A 0 B 1 C 2 D 3
3.采用简单随机抽样，从含有6个个体的总体中抽取一个容量为3的样本，个体a前两次未被抽到，第三次被抽到的概率为
A 
B 
C 
D 
4.已知定义在[-1，1]上的函数f(x)的值域为[-2，0]，则函数
的值域为
A [-1，1] B [-3，-1] C [-2，0] D 不能确定
5.已知
是偶函数，其定义域为[a-1,2a]，则点(a,b)的轨迹是
A 点 B 线段 C 直线 D 圆锥曲线
6.在计算机的算法语言中有一种函数
叫做取整函数（也称高斯函数），它表示
的整数部分，即[]是不超过的最大整数．例如：
．设函数
，则函数
的值域为
A.
B.
C. 
D. 
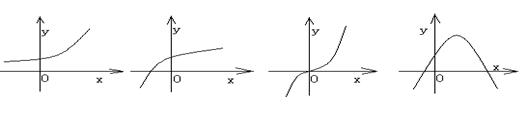
7.函数
的定义域是
,若对于任意的正数,函数
都是其定义域上的增函数,则函数的图象可能是
8.已知n次多项式
. 如果在一种计算中, 计算
(k=2,3,4,……, n)的值需要
次乘法, 计算
的值共需要9次运算(6次乘法, 3次加法). 那么计算
的值共需要__________次运算. 下面给出一种减少运算次数的算法: 
, 
, 利用该算法, 计算的值共需要6次运算, 计算的值共需要__________次运算.
9.对于函数f(x)=x2(x＞0)图象上任意两点A（a,a2）,B(b,b2),直线段AB必在曲线段AB的上方，设点C分
的比为
，则由图象的特征可得不等式
.请分析y=lgx的图象特征，类比上述不等式可以得到
10.参数方程
，则此直线的倾斜角为____________.
11.同学们都知道，在一次考试后，如果按顺序去掉一些高分，那么班级的平均分将降低；反之，如果按顺序去掉一些低分，那么班级的平均分将提高. 这两个事实可以用数学语言描述为：若有限数列
满足
，则
（结论用数学式子表示）.
12.身穿红、黄两种颜色衣服的各有两人，身穿蓝颜色衣服的有一人，现将这五人排成一行，要求穿相同颜色衣服的人不能相邻，则不同的排法共有
A.48种 B.72种 C.78种 D.84种
13.在4×□＋9×□=60的两个□中，分别填入两自然数，使它们的倒数和最小，应分别填上 和 。
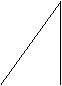
14.下面的一组图形为某一四棱锥S-ABCD的侧面与底面。
 |
 | |||||||||
 |  | ||||||||
 | | ||||||||
 |  | ||||||
 | |
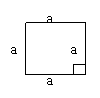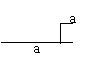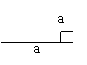（1）请画出四棱锥S-ABCD的示意图，是否存在一条侧棱垂直于底面？如果存在，请给出证明；如果不存在，请说明理由；
（2）若SA
面ABCD，E为AB中点，求二面角E-SC-D的大小；
（3）求点D到面SEC的距离。
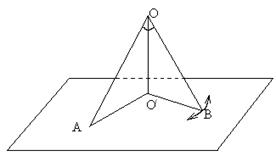
15．用硬纸剪出一个三边均不等的锐角三角形
，然后以边上的高
为折痕，折得两个直角三角形，使之直立于桌面上，那么，
就是角
在桌面上的射影，转动其中的一个直角三角形，观察与的大小关系，并说明理由
16.已知
之间满足
，动点(x,y)在曲线
(b>0)上变化，求x2+2y的最大值；
17.一个截面为抛物线形的旧河道，河口宽4米，河深2米，现要将其截面2改造为等腰梯形，要求河道深度不变，而且施工时只能挖土，不准向河道填土，试求当截面梯形的下底长为多少米时，才能使挖出的土最少？
18.在
中，
构成公差为正数的等差数列，且其周长为12,以
为x轴， 的中垂线为 y轴，建立直角坐标系,
(1)证明存在两定点E,F,使得BE+BF为定长；并求出点E,F的坐标及点B的轨迹C；
(2)设P为轨迹C 上的任一点，点M,N分别在射线PA,PC上，动点Q满足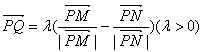
，经过点A且以
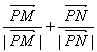为方向向量的直
与动点Q的轨迹交于点R ,试问：是否存在一个定点 D，使得
为定值？若存在求出点D的坐标；若不存在，说明理由？
19.已知正项数列满足
，且
.求证(1)
; (2)
20.某汽车厂有一条价值为a万元的汽车生产线，现要通过技术改造来提高该生产线的生产能力，提高产品的增加值．经过市场调查，产品的增加值y万元与技术改造投入x万元之间满足：①y与
和
的乘积成正比；②当
时，y=
．并且技术改造投入比率：
，其中t是常数，且
．
（1）设y=f（x），求f（x）的表达式及定义域；
（2）求出产品增加值y的最大值及相应的x的值．
21.已知函数
的定义域为I，导数
满足0＜＜2
且≠1，常数c1为方程
的实数根，常数c2为方程
的实数根．
（I）若对任意
，存在
，使等式
成立．试问：方程有几个实数根；
（II）求证：当
时，总有
成立；
（III）对任意
，若满足
，求证：
．
22.数列
的前
项和
,且
,
(
).
(1)求数列的通项;
(2)已知定理: “若函数
在区间
上是凹函数，
，且
存在，则有
”。若函数
在
上是凹函数，试判断
与
的大小； (3)求证：
.