上海交通大学附属中学2004年度外省市招生
数学试卷（第二次）
（本试卷满分100分，90分钟完成）
一、单项选择题：（本大题满分30分）本大题共有10个小题，每小题给出了代号为(A)、(B)、(C)、(D)四个答案，其中有且只有一个答案是正确的。请把正确答案的代号写在题后的圆括号内。每小题选对得3分；不选、错选或选出的代表字母超过一个（不论是否写在圆括号内），一律得零分。
1． 在Rt△ABC中，各边长都扩大了2倍，那么锐角A的正弦值（ ）
(A) 缩小了两倍 (B) 没有变化 (C) 扩大了两倍 (D) 可能扩大也可能缩小
2．方程组
的解为（ ）
(A) x=4，y=0 (B) x=0，y=0 (C) 无解 (D) 无限组解
3．已知a-2、b+1、c-5、d+8、e-7的平均数为m，那么a、b、c、d、e的平均数为（ ）(A) m+1 (B) m-1 (C) m+5 (D) m-5
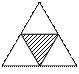
4．如下图，正三角形的三条中位线构成一个小的正三角形。如果小正三角形的面积（阴影部分）为25
，那么大的正三角形的周长为（ ）
(A) 60 (B) 100 (C) 60 (D) 100
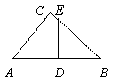
5．如图，在Rt△ABC中，∠C=90°，DE⊥AB，AC=BE=15，BC=20。则四边形ACED的面积为（ ）
(A) 54 (B) 75 (C) 90 (D) 96
6．如果(3，4)是反比例函数y=
图像上的一点，那么此函数必定经过点（ ）
(A) (2，6) (B) (2，-6) (C) (4，-3) (D) (3，-4)
7．已知⊙O的直径AB与弦AC的夹角为30°，过点C的切线PC与AB的延长线交于P。PC=5，则⊙O的半径为（ ）
(A) 
(B) 
(C) 5 (D) 10
8．一个凸n边形的内角中，恰有4个钝角，则n的最大值是（ ）
(A) 5 (B) 6 (C) 7 (D) 8
9．若a2+ma+18在整数范围内可分解为两个一次因式的乘积，则整数m不可能是（ ）
(A) ±9 (B) ±11 (C) ±12 (D) ±19
10．甲、乙两人分两次在同一粮店内买粮食，两次的单价不同，甲每次购粮100千克，乙每次购粮100元。若规定：谁两次购粮的平均单价低，谁的购粮方式就合算。那么这两次购粮（ ）
(A) 甲合算 (B) 乙合算 (C) 甲、乙一样 (D) 要看两次的价格情况
二、填空题：（本大题满分36分）本大题共有12个小题，各小题只要求在横线上方填写最终、最准确的结果，每题填写正确得3分，否则一律得0分。
11．若a、b、c三个数在数轴上对应点的位置如图所示，化简：
=
。
12．一个等腰梯形上底等于腰长，下底等于腰长的两倍，那么较小的内角大小为 。
13．某班一次测验成绩（10分制）如下：10分4人，9分7人，8分14人，7分18人，6分5人，5分2人。则本次测验的中位数是 。
14．已知函数
（c≠0）的对称中心为(a，b)，试回答：
的对称中心为
。
15．已知θ为锐角，且关于x的方程x2+3x+2sinθ=0的两根之差为
，则θ=
。
16．设∠xOy=30°，A是射线Ox上一点，OA=2，D为射线Oy上一点，OD=3，C是射线Ox上任意一点，B是射线Oy上任意一点，则折线ABCD的长AB+BC+CD的最小值是 。
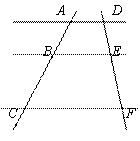
17．如图，AD∥BE∥CF，AB=AD=1，BE=2，CF=4，则BC= 。
18．在半径为5的单位圆中，直径AB与CD互相垂直，弦CH交AB于K，且CH=8，则│AK-BK│= 。
19．已知方程(x-19)(x-90)=p有实根r1，r2，其中p为实数，则方程(x-r1)(x-r2)=-p的最小实根是 。
20．王师傅围一块一面靠墙长方形花圃，面积为50m2，如果不靠墙的三面用竹篱笆去围。那么，竹篱笆最少需要 m长。
21．在数A的右端再加上一个数字6，则该数比原数增加2004，那么A=__ __。
22．对任意两个正整数x、y，定义一个运算“★”为x★y=2(x+2xy+y)，若正整数a、b满足a★b=1154，则有序正整数对(a，b)共有 对。
三、解答题：（本大题满分34分）本大题共3题，解答下列各题必须写出必要的步骤。
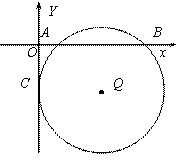
23．（本题满分10分）圆Q交x轴于原点右侧的A、B两点，并切y轴于原点下方的C点，如图所示。已知│AB│=3，│AC│=。（1）求A、B、C三点的坐标；（2）如果抛物线经过A、B、C三点，求这条抛物线的解析式。
24．（本题满分12分）一个完全平方数n的最后k（k≥2）位数字是相同的非零数字a，问：（1）a为哪个数字？（2）k最大为多少？（3）当k最大时，写出最小的具有这样性质的数（不必证明）。
25．（本题满分12分）如图，边长为a的菱形ABCD中，∠A=60°，过C任作直线分别交AB、AD的延长线于E、F，连接DE、BF交于M，若△BEM和△DFM外接圆的半径分别是R1、R2，求证：R1·R2为定值，并求这个定值。
参考答案：
一、选择题：
1、B；2、C ；3、A；4、A；5、D；6、A；7、B；8、C；9、C；10、B。
二、填空题：
11、3；12、60°；13、7.5；14、(3，4)；15、30°；16、
；17、2；18、7.5_；19、19；20、20；21、22；22、4。
三、解答题：
23、解：（1）设A(x，0)、B(x+3，0)、C(0，y)，
根据切割线定理，
。
解得：x=1或x=
（舍）。∴y=-2。
∴A、B、C三点的坐标分别是A(1，0)、B(4，0)、C(0，-2)。
（2）设过两点的抛物线为y=a(x-1)(x-4)，
∵它过点C(0，-2)，∴-2=a(0-1)(0-4)，∴a=
=
。
∴抛物线的方程为y=(x-1)(x-4)。
24、解：（1）一个平方数的末位数字（非0）只能是1，4，5，6，9。
∴数n的末二位必然是11，44，55，66，99，
又n为平方数，∴n≡0或1（mod 4）。
而末二位是11，55，99的数同余于3（mod 4），末二位是66的数同余于2（mod 4）。
∴a只能为4，如144=122。
（2）若至少有连续4个4，即n=m2=t·104+4444。
∴可设m=2m1，m12=25t·102+1111≡3（mod 4）。
同（1）可知，25t·102+1111不能为完全平方数。
∴至多连续3个4。（能够做到，见（3））
（3）当k最大时，最小的具有这样性质的数为1444=382。
25、证明：
△BEC∽△DCF，
∴
。
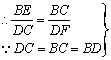∴△BED∽△DBF，
∴∠BED=∠DBM。
∴∠BME=∠BDM+∠DBM
=∠BDM+∠BED=∠ABD=60°。
∴由正弦定理得：2R1=
，2R2=
，
∴R1·R2=
·
=
=
。