绍兴一中高三数学（文科）模拟试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.
参考公式:
如果事件A、B互斥，那么
球的表面积公式
如果事件A、B相互独立，那么
球的体积公式
如果事件A在一次试验中发生的概率是P，那
么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
第Ⅰ卷 (选择题 共50分)
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．直线
的倾斜角为（ C ）
A．
B．
C．
D． 
2、已知集合A={2，a－1，a2}，B={9，－4，1－a}.如果A∩B={9}，则a的值为（ C ）
A． 3 B．—3 C．10 D．—10
3．已知奇函数
的定义域为[—2，a]，若
，则
的值为（ B ）
A．3
B．—3 C．
D．
4．函数
的反函数是 （ B
）
A．
B．
C．
D．
5．已知向量
，
，
，若
，则
等于（ D ）
A．
B．10 C．
D．5
6．二项式
的展开式中，系数最大的项是（ C ）
A．第三项 B．第四项 C．第五项 D．第四项或第五项
7．已知平面
都垂直于平面
，且
给出下列四个命题：
①若
；②若
；③若
；④若
.
其中真命题的个数为 （ A ）
A．4 B．3 C．2 D．1
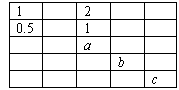
8. 在如图所示的表格中，每格填上一个数字后，使每一行成等差数列,每一列成等比数列,则a＋b＋c的值为 ( D )
A．4 B．3 C．2 D．1
9.
已知椭圆
与双曲线
有相同的焦点，则椭圆的离心率为( A
)
A.
B.
C.
D.
10
已知x y满足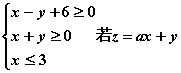
的最大值为
，最小值为
则a的范围为（ C
）
A 
B 
C 
D 
第Ⅱ卷 (非选择题 共100分)
二、填空题：本大题共4小题，每小题4分，共16分。
11．二项式
的展开式中常数项的值为____60____.
12．椭圆
的左焦点到右准线的距离为
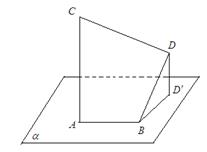
13．如图,线段AB在平面
内,线段
,线段
,线段
,
则BD与平面所成的角的大小为
;
14．某单位有六个科室，现从人才市场招聘来4名新毕业的大学生，现要将这四名大学生安排到其中的两个科室且每科室2名，则不同的安排方案种数为 90 (用数字作答).
三、解答题：本大题共6小题，每小题14分，共84分。解答应写出文字说明，证明过程或演算步骤。
15．已知函数
，
（1）求
的值；
（2）求函数
的最大值及相应的
的集合；
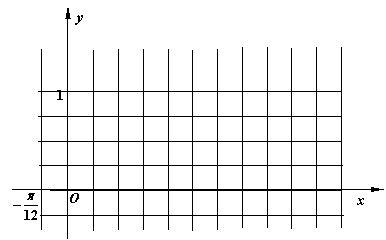
（3）画出函数在
内的图像;
解：（1）
；
（2）
…………………………………4分
当
时，的最大值为
，此时的集合为
…8分
（3）列表：
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点：连线：（略）……………………………………………………14分
16设Sn是首项为4, 公差d¹0的等差数列{ a n}的前n项和，若
S3和
S4的等比中项为
S5. 求:
（1）{ a n}的通项公式an； （2）使Sn> 0的最大n值.
解：由条件得:
,
…………4分
∵S n = a1n +
n（n – 1）d,
∴
, ∵d ¹ 0 ,得
,
∴an = 
. ………………9分
（2）由an = ³0,
得n £
, ∴n = 2时, Sn取最大值,
∴使Sn> 0的最大n的值为4. ……………… 14分
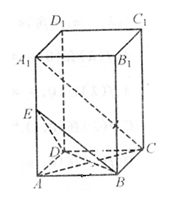
17．已知正四棱柱ABCD—A1B1C1D1底面边长为2，AA1=4，点E在AA1上，AC与BD交于点O；
（1）若EA=2，求证：A1C//平面EBD；
（2）若EA=3，求二面角A—DE—B的正切值；
（3）在AA1上是否存在点E，使异面直线EB与AC所成的角为300？若存在，试确定E点的位置，否则说明理由。
解：（1）证明A1C//EO即可；
（2）
（3）不存在，可用向量法；
18.经统计，某大医院一个结算窗口每天排队结算的人数及相应的概率如下：
| 排队人数 | 0—5 | 6—10 | 11—15 | 16—20 | 21—25 | 25人以上 |
| 概 率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
(1)每天不超过20人排队结算的概率是多少？
(2)一周7天中，若有3天以上（含3天）出现超过15人排队结算的概率大于0.75，医院就需要增加结算窗口，请问该医院是否需要增加结算窗口？
解：（1）每天不超过20人排队结算的概率为:P=0.1+0.5+0.25+0.25=0.75，即不超过20人排队结算的概率为0.75.------------4分
（2）每天超过15人排队结算的概率为:0.25+0.2+0.25=
,-------------8分
一周7天中，没有出现超过15人排队结算的概率为C
（）7；
一周7天中，有一天出现超过15人排队结算的概率为C
（）（）7；
一周7天中，有二天出现超过15人排队结算的概率为C
（）2（）5；
所以有3天或3天以上出现超过15人排队结算的概率为：
1-［C()7+C()()6+C()2()5］=
＞0.75,---------13分
所以，该医院需要增加结算窗口.--------------14分
19．已知函数
处取得极值，曲线
过原点O（0，0）和点
P（－1，2），若曲线
在点P处的切线l与直线
的夹角为45°，且l的倾斜角为钝角.
（Ⅰ）求的解析式；
（Ⅱ）若在区间[2m－1，m+1]上是增函数，求m的取值范围.
解：（I）∵曲线过原点，所以d=0；
∵过点P（－1，2）的切线l的斜率为
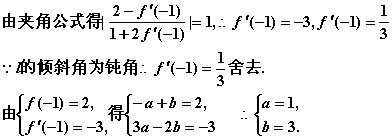
（a,b,c,d每求对一个得2分，共8分）
（II）
——————————14分
20．在平面直角坐标系中，O为坐标原点，已知点
，
，若点C满足
，点C的轨迹与抛物线
交于A、B两点；
（1）求点C的轨迹方程；
（2）求证：
；
（3）在x轴正半轴上是否存在一定点
，使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍，若存在，求出m的值；若不存在，请说明理由.
解：（1）设
，由
知，点C的轨迹为
…2分
（2）由
消y得：
设
，
，则
，
………………………………5分
所以
，所以
，于是………………7分
（3）假设存在过点P的弦EF符合题意，则此弦的斜率不为零，设此弦所在直线的方程为
由
消x得：
，设
，
，
则
，
……………………10分
因为过点P作抛物线的弦的长度是原点到弦的中点距离的2倍，所以
即
所以
得
，所以存在……………………………………14分