



2005年全国高中数学联赛(吉林赛区)预赛参考答案
一、选择题
1.D; 2.C ; 3.A; 4.B; 5.D; 6.A
二、填空题
1. ![]() ; 2.
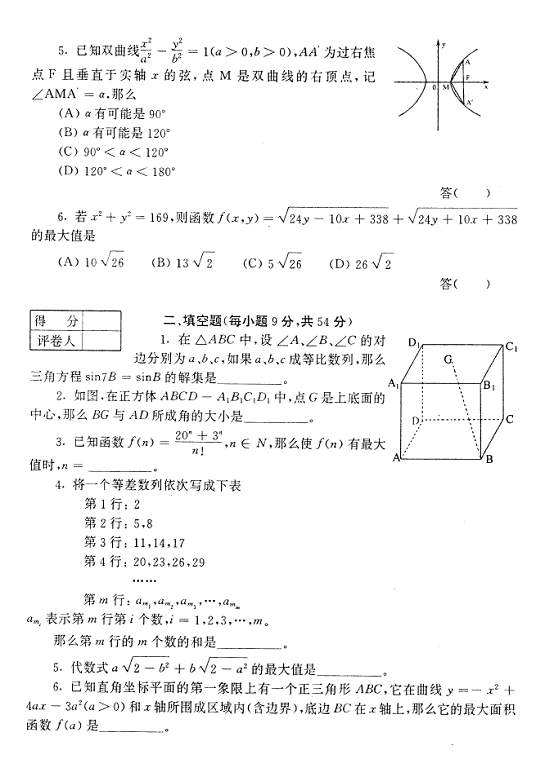
; 2. ![]()
![]() ; 3.
; 3. ![]() ; 4.
; 4. ![]() ; 5.
; 5. ![]() 6. 当
6. 当![]() ≥
≥![]() 时,
时,![]() ;当
;当![]() <
<![]() <
<![]() 时,
时,![]()
三、1.在直角坐标平面中,![]() 的两个顶点
的两个顶点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,平面内两点
,平面内两点![]() 同时满足下列条件:①
同时满足下列条件:①![]() ;②
;②![]() ;③
;③![]() ∥
∥![]()
(1)求![]() 的顶点
的顶点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线
的直线![]() 与(1)中轨迹交于
与(1)中轨迹交于![]() 两点,求
两点,求![]() 的取值范围
的取值范围
解:(1)设![]()
![]()
![]() 点在线段
点在线段![]() 的中垂线上
的中垂线上
由已知![]()
又![]() ∥
∥![]()
![]()
又![]()
![]()
![]()
![]()
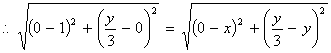
![]()
![]()
![]() 顶点
顶点![]() 的轨迹方程为
的轨迹方程为![]()
![]()
(2)设直线![]() 方程为:
方程为:![]() ,
,![]() ,
,![]()
由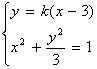 消去
消去![]() 得:
得:![]() ①
①
![]() ,
, ![]()
而![]()
![]()
![]()
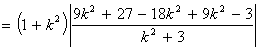
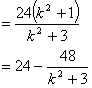
由方程①知 ![]() >
>![]()
![]() <
<![]()
![]()
![]() <
<![]() <
<![]()
![]()
![]()
四、若![]()
![]()
![]() 为复数集1≤
为复数集1≤![]() ≤
≤![]() ,且对
,且对![]() ≤
≤![]() ≤
≤![]()
![]() 都有
都有![]()
求证:对一切正整数![]() 都有
都有![]()
证明:设![]()
![]()
易知![]()
即:![]()
![]()
……
![]()
则![]()
由已知![]() ≤
≤![]() ≤
≤![]() 都有
都有![]() ,可得
,可得![]() 即
即![]()
故![]() 有零根,不妨设为
有零根,不妨设为![]() ,
,
反复上述方法可得:
![]()
![]()
故对一切正整数![]() 都有
都有![]()
五、求满足![]() 的最小正整数
的最小正整数![]()
解:设![]() ,
,![]() ,
,![]() 则
则
![]()
易知![]() ,故
,故
由![]() ,故可设
,故可设![]()
由![]() ,下证
,下证![]()
![]()
当![]() 时, 上式显然成立
时, 上式显然成立
假定![]() 时,有
时,有![]() ,
,
则 当![]() 时
时
![]()
易知 ![]() , 以及
, 以及 ![]()
![]()
则 ![]() ≥
≥![]()
![]() ≥
≥![]()
从而使![]() 的最小正整数
的最小正整数![]() 为
为![]()
六、一个正方形被剖分为4个正方形,剖分图的边数为12,若一个正方形被剖分为2005个凸多边形,试求剖分图中边数的最大值。
解:由欧拉定理可知,简单多面体的顶点数![]() ,面数
,面数![]() ,棱数
,棱数![]() 有关系:
有关系:![]()
由欧拉定理容易看出,若一个凸多边形被剖分为![]() 个凸多边形,则剖分图中的顶点数
个凸多边形,则剖分图中的顶点数![]() ,多边形数
,多边形数![]() ,边数
,边数![]() 有关系:
有关系: ![]() (1)
(1)
下面在一般的情况下,即正方形被剖分为![]() 个凸多边形时,求剖分图中边数的最大值,设剖分图中的顶点数为
个凸多边形时,求剖分图中边数的最大值,设剖分图中的顶点数为![]() ,多边形数为
,多边形数为![]() ,边数为
,边数为![]()
(一)先求边数的上界
设原正方形的4个顶点是![]() ,若凸多边形的顶点V
,若凸多边形的顶点V![]() 则易知
则易知
![]() ≥
≥![]() (这里用
(这里用![]() 表示通过顶点
表示通过顶点![]() 的边数),于是有
的边数),于是有 ![]() ≤
≤![]()
这样的顶点![]() 有
有![]() 个,于是有
个,于是有![]() 个上面的不等式,将它们相加求和,并注意到除去正方形四边的每条边恰是两个凸多边形的边,有
个上面的不等式,将它们相加求和,并注意到除去正方形四边的每条边恰是两个凸多边形的边,有
![]()
≤![]()
即有 ![]() ≥
≥![]()
因为 ![]() ≥
≥![]() ,
,![]() ≥
≥![]() ,
,![]() ≥
≥![]() ,
,![]() ≥
≥![]() ,
,
所以 ![]() ≥
≥![]() (2)
(2)
由公式(1),有
![]() ,
,
![]() (3)
(3)
将(2)式代入(3)式,并整理有
![]() ≤
≤![]()
![]() ≤
≤![]() (4)
(4)
(二)构造例子,使边数![]()
过正方形的一边相继作![]() 条邻边的平行线,正方形被剖分为
条邻边的平行线,正方形被剖分为![]() 个矩形,
个矩形,
易知,边数
![]()
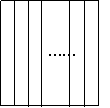 综合两方面,剖分图中边数的最大值为
综合两方面,剖分图中边数的最大值为![]() ,所以正方形剖分为
,所以正方形剖分为![]() 个凸多边形的边数最大值为
个凸多边形的边数最大值为![]()