江苏省清江中学2005-2006学年度第一学期高三期末考试数学模拟试卷(1)
一、选择题:(每小题5分,12小题,共60分)
1下列命题中:⑴ 函数![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称;⑵ 若
对称;⑵ 若![]() ,则函数
,则函数![]() 的图象关于原点对称;⑶ 若
的图象关于原点对称;⑶ 若![]() ,则
,则![]() 的图象关于
的图象关于![]() 轴对称;⑷ 函数
轴对称;⑷ 函数![]() 的图象与
的图象与![]() 的图象关于
的图象关于![]() 轴对称.
轴对称.
其中真命题是(D)
A ⑵⑶ B ⑵⑶⑷ C ⑴⑵⑶ D ⑴⑵⑶⑷
2 设![]() ,函数
,函数![]() 的反函数和
的反函数和![]() 的反函数的图象关于(B)
的反函数的图象关于(B)
A ![]() 轴对称 B
轴对称 B ![]() 轴对称 C 直线
轴对称 C 直线![]() 对称 D 原点对称
对称 D 原点对称
3 点P(![]() )在角α的终边上,则角α的值为(D)
)在角α的终边上,则角α的值为(D)
A ![]() B
B
![]() C
C ![]() D
D ![]()
4 设![]() 是三角形的内角,若函数
是三角形的内角,若函数![]() 对一切实数
对一切实数![]() 都有
都有![]() ,则
,则![]() 的取值范围是 (B)
的取值范围是 (B)
A ![]() B
B
![]() C
C ![]() ∪
∪![]() D
D ![]()
5 若定义在R上的偶函数![]() 满足
满足![]() ,且在[
,且在[![]() ]上是减函数,α、β是锐角三角形的两个内角,则 (A)
]上是减函数,α、β是锐角三角形的两个内角,则 (A)
A ![]() B
B ![]()
C ![]() D
D
![]()
6 为得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象(D)
的图象(D)
A 向左平移![]() 个单位
B 向右平移
个单位
B 向右平移![]() 个单位
个单位
C 向左平移![]() 个单位
D向右平移
个单位
D向右平移![]() 个单位
个单位
7 在△ABC中,![]() ,
,![]() ,若
,若![]() ,则三角形ABC是(C)
,则三角形ABC是(C)
A 锐角三角形 B 直角三角形 C 钝角三角形 D 等腰直角三角形
8 将函数![]() 的图象按向量
的图象按向量![]() 平移,得到
平移,得到![]() 的图象,则
的图象,则![]() 的坐标为(B)
的坐标为(B)
A ![]() B
B
![]() C
C
![]() D
D
![]()
9 已知数列![]() (
(![]() *)中,
*)中,![]() ,
,![]() ,则这个数列的第
,则这个数列的第![]() 项为(C)
项为(C)
A ![]() B
B
![]() C
C ![]() D
D ![]()
10 设双曲线![]() (
(![]() )的半焦距为
)的半焦距为![]() ,直线
,直线![]() 过(
过(![]() ),(
),(![]() )两点,已知原点到直线
)两点,已知原点到直线![]() 的距离为
的距离为![]() ,则双曲线的离心率为(A)
,则双曲线的离心率为(A)
A
2
B ![]() C
C ![]() D
D
![]()
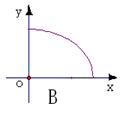
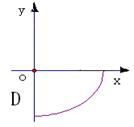
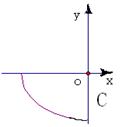
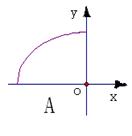 11 若
11 若![]() ,则椭圆
,则椭圆![]() 的中心的轨迹是(D)
的中心的轨迹是(D)
12 在边长为![]() 的菱形ABCD中,∠BAD=
的菱形ABCD中,∠BAD=![]() ,将△BAD绕BD旋转
,将△BAD绕BD旋转![]() 后点A到达点A/,则三棱锥A/-BCD的体积为(B)
后点A到达点A/,则三棱锥A/-BCD的体积为(B)
A
![]() B
B
![]() C
C ![]() D
D ![]()
二、填空题:(每小题4分,4小题,共16分)
13 若存在常数![]() ,使得函数
,使得函数![]() 满足
满足![]() (
(![]() )恒成立,则
)恒成立,则![]() 的一个正周期为____
的一个正周期为____![]() ____
____
14 设A=![]() ,B=
,B=![]() ;
;
⑴ 若A∩B=φ,则满足条件的![]() 组成的集合是_______
组成的集合是_______![]() _____
_____
⑵ 若A∩B为单元素集,则满足条件的![]() 组成的集合是___
组成的集合是___![]() ___
___
15 已知F1,F2分别是椭圆![]() (
(![]() )的两焦点,点P在椭圆上,△POF2是面积为
)的两焦点,点P在椭圆上,△POF2是面积为![]() 的正三角形,则
的正三角形,则![]() 的值是____
的值是____![]() ________
________
16一同学在电脑中打出如下若干个圆(图中●表示实圆,○表示空心圆):
●○●●○●●●○●●●●○●●●●●○……若将此若干个圆依次规律继续下去得到一系列圆,那么在前2004个圆中有 61 个空心圆.
三、解答题:
17 解关于![]() 的不等式
的不等式![]() (
(![]() )
)
解:原不等式可化为: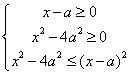
![]()
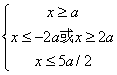
![]()
∴ 原不等式的解集为![]() 。
。
18 在△ABC中,角A、B、C的对边分别为![]() 、
、![]() 、
、![]() ,若△ABC的外接圆的半径R=
,若△ABC的外接圆的半径R=![]() ,且
,且![]() ,分别求出B和
,分别求出B和![]() 的大小。
的大小。
解:在△ABC中,由正弦定理知:![]()
∴![]()
![]()
![]()
∴![]() 可化为:
可化为:![]()
整理得:![]()
又![]() ∴
∴![]()
![]()
![]()
![]()
∴![]()
19 在正四棱锥P-ABCD中,AB=![]() ,E为PD的中点,O为底面ABCD的中心,侧面PAD与底面ABCD所成的角二面角为600。
,E为PD的中点,O为底面ABCD的中心,侧面PAD与底面ABCD所成的角二面角为600。
⑴ 证明:AC⊥平面PBD;
⑵ 求异面直线EA与PC所成的角的正切值。
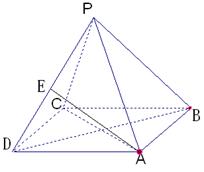
① 证明:连PO,易证:PO⊥面ABCD
∴PO⊥AC
又AC⊥BD,BD和PO是面PBD内的两相交直线
∴AC⊥面PBD
② 解:以O为原点,过AD的中点M的射线为![]() 轴,过AB中点N的射线为
轴,过AB中点N的射线为![]() 轴,
轴,
OP为![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系
设A![]() ,P
,P![]() ,D
,D![]() ,C
,C![]()
∴E![]() ,
,
∴![]() ),
),![]()
∴ ![]()
∴![]()
20设等比数列![]() 中,公比
中,公比![]() ,
,![]() ,
,![]() 。
。
⑴ 用![]() ,
,![]() ,
,![]() 表示
表示![]() ;
;
⑵ 若![]() ,
,![]() ,
,![]() 成等差数列,求
成等差数列,求![]() ;
;
⑶ 在⑵的条件下,设![]() ,
,![]() ,求证:
,求证:![]()
解:①
由题意得:![]() ,
,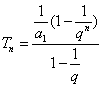
∴ ![]()
② 由题意:2![]()
![]()
![]()
![]()
![]()
![]()
③ 由②知道:![]()
∴ ![]()
![]()
两式相减得:![]()
∴![]()
21 甲、乙容器中有浓度为25%和75%的盐酸溶液各8克,从甲溶液往乙容器倒入4克溶液,摇匀后,再从乙容器往甲容器倒入4克溶液为一次操作,这样的操作反复进行。
⑴ 求操作![]() 次后,甲容器与乙容器中的纯盐酸分别为多少克?
次后,甲容器与乙容器中的纯盐酸分别为多少克?
⑵ 欲使甲容器中的溶液浓度大于48%,问至少操作多少次?
解:①设操作![]() 次后,甲、乙两容器中的纯盐酸分别为
次后,甲、乙两容器中的纯盐酸分别为![]() 、
、![]() 克
克
则:![]()
![]()
![]()
而![]()
∴![]()
![]()
∴![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列
的等比数列
∴![]()
![]()
![]()
![]()
② 依题意:![]()
![]()
![]()
![]()
![]()
又![]() 为自然数
为自然数
∴![]() 的最小值为3
的最小值为3
故至少3次能达到要求。
22 已知函数![]() (
(![]() ),当
),当![]() 时,
时,![]() ≤1。
≤1。
⑴ 求证:![]() ;
;
⑵ 设![]() ,证明:当
,证明:当![]() 时,
时,![]() ;
;
⑶ 若![]() ,
,![]() ,求实数
,求实数![]() 的值。
的值。
① 证明:∵![]()
∴![]()
![]()
![]()
∴![]()
又当![]() 时,
时,![]() ≤1
≤1
∴![]() ,
,![]()
∴![]()
![]()
![]()
② 由①知:![]()
![]()
![]()
∴![]()
![]()
又![]() 时,
时,![]() ,
,![]() ,
,![]()
∴![]()
![]()
![]()
![]()
![]()
= ![]()
≤2
③ ∵![]() 时,
时,![]() ≤1
≤1
∴![]() 时,
时,![]() 的最大值小于或等于1,
的最大值小于或等于1,![]() 的最小值为
的最小值为![]()
又![]() ,
,![]()
∴![]() 在
在![]() 时取得最小值-1
时取得最小值-1
∴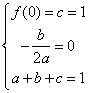
![]()