江苏武进中学高三数学专题练习一
组题人:袁兆华 审核人: 2006.1
一、选择题：(每题5分，共60分)
1．已知a为不等于零的实数，那么集合
的子集的个数为
A．1个 B．2个 C．4个 D．1个或2个或4个
2．函数
的最小正周期是
A．
B．π
C．2π D．3π
3．已知关于x的不等式
的解集是[-1，0）则a+b=
A．－2 B．－1 C．1 D．3
4．过双曲线
的右焦点作直线l交双曲线于A、B两点，若
=4，则满足条件的直线l有
A．2条 B．3条 C．4条 D．无数条
5．若向量
的夹角是
A．30° B．60° C．90° D．120°
6．设a、b是两条异面直线，P是a、b外的一点，则下列结论正确的是
A．过P有一条直线和a、b都平行；B．过P有一条直线和a、b都相交；
C．过P有一条直线和a、b都垂直；D．过P有一个平面和a、b都垂直。
7．互不相等的三个正数
成等比数列，且点
P1（
共线
则
，
A．等差数列，但不等比数列； B．等比数列而非等差数列
C．等比数列，也可能成等差数列 D．既不是等比数列，又不是等差数列
8．若从集合P到集合Q=
所有的不同映射共有81个，则从集合Q到集合P可作的不同映射共有
A．32个 B．27个 C．81个 D．64个
9．对于函数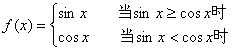
给出下列四个命题：
①该函数的值域为[-1，1]
②当且仅当
③该函数是以π为最小正周期的周期函数；
④当且仅当
上述命题中错误命题的个数为
A．1 B．2 C．3 D．4
10．已知等差数列
，那么，一定有
A．
C、
二、填空题：(每題4分，共16分)
11、若
,则
的值是
.
12、不等式
对一切非零实数x恒成立 , 则
的取值范围是 .
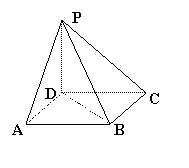
13、如图，底面ABCD是正方形,PD
平面ABCD,PD=AD,
则PA与BD所成的角等于 .
14、若函数
在区间
上是减函数，
则实数
的取值范围是
。
南阳中学高三数学第二十周练周练答题卡
姓名:________________ 考号:________________
一、选择题：(每题5分，共60分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二、填空题：(每題4分，共16分)
11 12
13 14
三、解答题：
15．(本题满分10分)已知，α是锐角，且tan
（2）
的值
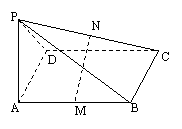16．(本题满分12分)如图，PA⊥矩形ABCD所在平面，PA=AD=a，M，N分别是AB，PC的中点，（1）求证：MN⊥平面PCD
（2）若AB=
17. (本题满分12分)（1）设
M(
互相垂直的弦MP、MQ，求证：PQ恒过定点M'（
（2）直线
点M，使得△MPQ为以PQ为斜边的直角三角形？
南阳中学高三数学第二十周练周练答案及评分建议
一、选择题：(每题5分，共60分)
1．D 2. A 3.C 4.B 5.C 6.C 7.C 8.D 9.D 10.B
二、填空题：(每题4分，共16分)
11.
；12.
；13.
；14.
三、解答题：
15．解：（1）
由
=2，有
=2
解得
（2）原式=
16．（1）证明：取PD中点E，∵E，N分别是PD，PC中点，
∴ 
∥MN
∵PA=AD ∴AE⊥PD
又∵PA⊥平面ABCD ∴PA⊥CD，CD⊥AD （4'）
PA∩AD=A ∴CD⊥平面PAD
AE平面PAD ∴AE⊥CD，CD∩PD=D
∴AE⊥平面PCD ∴MN⊥平面PCD （6'）
（2）解：连AC交BD于O，则O是AC中点，连ON则ON⊥ABCD （8'）
作OF⊥MD，连NF，则NF⊥MD
∴∠NFO是二面角N—DM——C的平面角，
NO=
（10'）
∠NFO=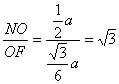
二面角N—MD——C为60° (12’)
17（1）证明：设PQ的方程为
得 
其中
（3'）
即
∴
直线PQ的方程为
即
（6'）
（2）设M（
上，所以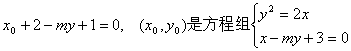
的解，消去x得
。 （12'）