|
2004-2005学年度下学期
高中学生学科素质训练
高三第二轮复习数学综合测试卷(1)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。考试时间120分钟。
第Ⅰ卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4πR2
如果事件A、B相互独立,那么 其中R表示球的半径
P(A·B)=P(A)·P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P. ![]()
那么n次独立重复试验中恰好发生k次的概 其中R表示球的半径
率![]()
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合![]() ,集合
,集合![]() ,则
,则![]() 是
是
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 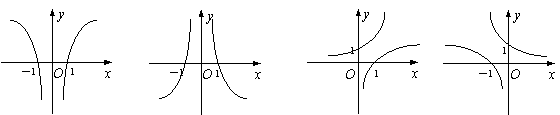 函数y=log2 x 的图象大致是 ( )
函数y=log2 x 的图象大致是 ( )
A. B. C. D.
3.动直线![]() 所围区域的边界的曲线是 ( )
所围区域的边界的曲线是 ( )
A. 直线 B. 线段 C. 单位圆 D. 部分单位圆
4.函数y=sin2x的图象按向量a平移后,所得函数的解析式是y=cos2x+1,则a等于( )
A.(![]() ,1) B. (-
,1) B. (-![]() ,1) C. (-
,1) C. (-![]() ,1) D.
(
,1) D.
(![]() ,1)
,1)
5.已知等比数列![]() 的各项均为正数,公比
的各项均为正数,公比![]() Q=
Q=![]() ,则P与Q
,则P与Q
的大小关系是 ( )
A.P>Q B.P<Q C.P=Q D.无法确定
6.口袋里装有大小相同的黑、白两色的手套,黑色手套15只,白色手套10只.现从中随机地取出两只手套,如果两只是同色手套则甲获胜,两只手套颜色不同则乙获胜. 试问:甲、乙获胜的机会是 ( )
A. 甲多 B. 乙多 C. 一样多 D. 不确定的
7.若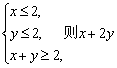 的取值范围是 ( )
的取值范围是 ( )
A.[2,6] B.[2,5] C.[3,6] C.[3,5]
8.已知直二面角![]() ,直线
,直线![]() ,直线
,直线![]() ,且
,且![]() 与
与![]() 不垂直,
不垂直,![]() 与
与![]() 不垂直,那么 ( )
不垂直,那么 ( )
A.![]() 与
与![]() 可能垂直,但不可能平行 B.
可能垂直,但不可能平行 B.![]() 与
与![]() 可能垂直,也可能平行
可能垂直,也可能平行
C.![]() 与
与![]() 不可能垂直,不可能平行 D.
不可能垂直,不可能平行 D.![]() 与
与![]() 不可能垂直,但可能平行
不可能垂直,但可能平行
9.若以圆锥曲线的一条经过焦点的弦为直径的圆与对应的准线无公共点,则此圆锥曲线为
( )
A.双曲线 B.椭圆 C.抛物线 D.椭圆或双曲线
10.我们用记号![]() 来表示复数cosq +isinq,即
来表示复数cosq +isinq,即![]() (其中e= 2.71828…是自然对数的底数,q 的单位是弧度).则:
(其中e= 2.71828…是自然对数的底数,q 的单位是弧度).则:
①
![]() ; ②
; ② ![]() ; ③
; ③ ![]() .
.
其中正确的式子代号为 ( )
A.① B.①② C.①③ D.②③
11.设![]() 是平面直角坐标系中一个面积有限图形M的边界的方程,则
是平面直角坐标系中一个面积有限图形M的边界的方程,则![]() 围成的图形面积是M的面积的 ( )
围成的图形面积是M的面积的 ( )
A.![]() 倍 B.
倍 B.![]() 倍
C.1倍 D.4倍
倍
C.1倍 D.4倍
12.如图所示的雕塑组合:下面是棱长为2米的正方体基座,基座上面中心位置安放着一个大球,阳光从A面正前方照下时,基座在B面正前方地面的影长是4.8米,此时大球影子最远点伸到距B面8.8米处,则大球体积是 ( )
A.![]() B.
B.![]() D.
D.![]() D.
D.![]()

A面 B面
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.答案填在题中横线上.
13.一种专门占据内存的计算机病毒,开机时占据内存![]() KB,然后每
KB,然后每![]() 分钟自身复制一次,复制后所占内存是原来的
分钟自身复制一次,复制后所占内存是原来的![]() 倍,那么开机后经过 ______ 分钟,该病毒占据
倍,那么开机后经过 ______ 分钟,该病毒占据![]() MB内存.(
MB内存.(![]() MB=
MB=![]() KB)
KB)
14.若圆锥的高为10cm,过顶点作与底面成45°的平面恰好把圆锥底面周长截去,则这截面的面积为 .
15.设![]() 、
、![]() ,常数
,常数![]() ,定义运算
,定义运算![]() ,
,
若![]() ,则动点
,则动点![]() 的轨迹方程是__________________.
的轨迹方程是__________________.
16.一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示。(至少打开一个水口)
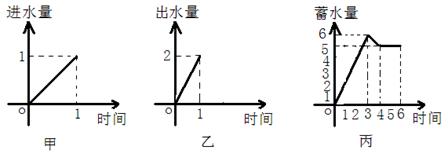 |
给出以下![]() 个论断:
个论断:
①![]() 点到
点到![]() 点只进水不出水;②
点只进水不出水;②![]() 点到
点到![]() 点不进水只出水;③
点不进水只出水;③![]() 点到
点到![]() 点不进水不出水.
点不进水不出水.
则一定不确定的论断是___________.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
在![]() 中,内角A、B、C的对边分别为a、b、c,已知
中,内角A、B、C的对边分别为a、b、c,已知![]() ,
,![]() ,求角A的取值范围.
,求角A的取值范围.
注意:考生在(18甲)、(18乙)两题中选一题作答,如果两题都答,只以(18甲)计分.
18.(本小题满分12分)
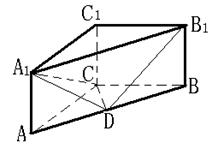 (甲)如图,已知直三棱柱
(甲)如图,已知直三棱柱![]() 中,
中,![]() 是
是![]() 上的一个点,且
上的一个点,且![]() .
.
(Ⅰ)分别以射线![]() 、
、![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴、
轴、
![]() 轴建立空间直角坐标系,求
轴建立空间直角坐标系,求![]() 点的坐标;
点的坐标;
(Ⅱ)求![]() 与平面
与平面![]() 所成的角的大小(用
所成的角的大小(用
反三角表示).
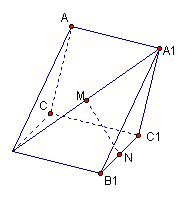 (乙)已知:如图,直三棱柱ABC—A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别为A1B、B1C1的中点.
(乙)已知:如图,直三棱柱ABC—A1B1C1中,AC⊥BC,AC=BC=CC1,M、N分别为A1B、B1C1的中点.
(Ⅰ)求证:MN//平面ACC1
(Ⅱ)求证:MN⊥平面A1BC;
(Ⅲ)求二面角A—A1B—C的大小.
19.(本小题满分12分)
 一个电路中有三个电子元件,它们接通的概率都是m(0<m<1
一个电路中有三个电子元件,它们接通的概率都是m(0<m<1![]() 如图,有如下三种联接方法:
如图,有如下三种联接方法:
![]()
![]() ①
②
③
①
②
③
(I)分别求出这三种电路各自接通的概率;
(II)试分析这三种电路哪种性能最优,并证明你的结论.
20.(本小题满分12分)
一片小树林有4000棵树,每年将砍伐20%的树木并种植1000棵树,设n年后所剩树木的棵数为![]() ,
,
(I)计算![]() 的值;
的值;
(II)请猜想数列{an}的通项公式,并加以证明;
(III)试判断经过若干年后,树木的棵数能否大体稳定在某一固定值上?并说明理由.
21.(本小题满分14分)
已知动点![]() 与双曲线
与双曲线![]() 的两个焦点
的两个焦点![]() 、
、![]() 的距离之和为定值,且
的距离之和为定值,且![]()
![]() 的最小值为
的最小值为![]() .
.
(I)求动点![]() 的轨迹方程;
的轨迹方程;
(II)若已知![]() ,
,![]() 、
、![]() 在动点
在动点![]() 的轨迹上且
的轨迹上且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
22.(本小题满分14分)
已知![]() 上是增函数,在[0,2]上是减函数,且方程
上是增函数,在[0,2]上是减函数,且方程
![]() 有三个根,它们分别为
有三个根,它们分别为![]() .
.
(Ⅰ)求c的值;
(Ⅱ)求证![]()
(Ⅲ)求![]() 的取值范围.
的取值范围.
参考答案(1)
一、选择题
1.C. 2.A. 3.C. 4.B. 5.A. 6.C. 7.A. 8.D. 9.B 10.C 11.A 12.A.
提示:
1.![]()
2.函数![]() 是偶函数,且在
是偶函数,且在![]() 上是增函数.
上是增函数.
3.方程![]() 是单位圆
是单位圆![]() 的切线系方程.
的切线系方程.
4.在同一坐标系内画出函数![]() 与
与![]() 的图象即可.
的图象即可.
5.由正项等比数列的性质可知:![]()
![]() ,且
,且![]()
![]() .
.
6.两只是同色手套的种数为![]() 两只不是同色手套的种数为:
两只不是同色手套的种数为:![]()
7.由![]() 得
得 ![]() 又
又![]() 所以当
所以当![]() 时,原不等式组成立,从
时,原不等式组成立,从
而![]()
8. 用逐选支排除法.
9. 圆锥曲线的离心率![]() 的性质可得,只有椭圆的焦点 长小于它的两端点到其对应准线的距离的和.
的性质可得,只有椭圆的焦点 长小于它的两端点到其对应准线的距离的和.
10.由已知得![]()
![]()
11.由![]() 与
与![]() 的关系知,在
的关系知,在![]() 中的
中的![]() 与
与![]() 的取值范围缩小到原来的
的取值范围缩小到原来的![]() ,于是其区域的面积就缩小到原来的
,于是其区域的面积就缩小到原来的![]()
12.由相似三角形(图略),得 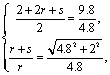 解出球半径
解出球半径 ![]()
二、填空题 13.45. 14. ![]()
![]() . 15.
. 15.![]()
![]() . 16.②③.
. 16.②③.
提示:13. 设第n个3分种复制的病毒为![]() KB,则
KB,则![]()
![]() KB,于是
KB,于是
![]() ,解出
,解出![]()
14.画图后应用面与面的夹角公式以及圆的性质、三角形面积公式可计算得.
15.由![]() ,得
,得 ![]()
![]() .
.
16.由图甲知,一个进水管在1小时内可进1单位水,所以由0点到3点两只进水管只进水,不出水;由图乙知,出水管在1小时内可出水2单位,在3点到4点只出水1单位,所以从 3点到4点开一个进水管,一个出水管; 由图丙知, 从4点到6点可同时开两个进水管,一个出水管,此时进水与出水也可保持平衡.
三、解答题
17.由正弦定理得:
![]() ,…………2分 又
,…………2分 又![]() ,
,
所以![]() ,…………6分
,…………6分
化简得![]() ,…………8分
,…………8分
![]() .…………10分 又
.…………10分 又![]() ,
,
故![]() 或
或![]() ………………12分
………………12分
18.(甲小题)
(I) 设![]() ,则
,则![]() ,得
,得![]() , ………… 2分
, ………… 2分
∴![]() ,
,![]() ,
,![]() ,
,![]() .……………4分
.……………4分
∴![]() ,
,![]() ,……………6分
,……………6分
∵![]() ,∴
,∴![]() ,得
,得![]() , ∴
, ∴![]() .……………7分
.……………7分
(II) 过![]() 作
作![]() ,∵平面
,∵平面![]() 平面
平面![]() ,
,
∴![]() ,…………9分
,…………9分
连![]() ,则
,则![]() 是
是![]() 与平面
与平面![]() 所成角, …………12分
所成角, …………12分
![]() (12分),
(12分),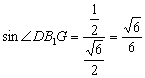 ,
,
∴![]() ,即
,即![]() 与平面
与平面![]() 所成角为
所成角为![]() . ………14分
. ………14分
18(乙小题)(Ⅰ)连AC1,AB1.
由直三棱柱的性质,得AA1⊥平面A1B1C1,
∴AA1⊥A1B1,则四边形ABB1A1为矩形. ……………………2分
由矩形性质得,AB1过A1B的中点M.
在△AB1C1中,由中位线性质,得MN//AC1.
又AC1![]() 平面ACC1A1,MN
平面ACC1A1,MN![]() 平面ACC1A1,
平面ACC1A1,
∴MN//平面ACC1A1. …………… …………4分
(Ⅱ)BC⊥平面ACC1A1,AC1![]() 平面ACC1A1,
平面ACC1A1,
∴BC⊥AC1 在正方形ACC1A1中,A1C⊥AC1
又BC∩A1C=C,∴AC1⊥平面A1BC.………………………7分
由MN//AC1,∴MN⊥平面A1BC.…………………………8分
(Ⅲ)作CE⊥AB于E.
∵平面ABC⊥平面ABB1A1,∴CE⊥平面ABB1A1
作EF⊥A1B于F,连FC. 由三垂线定理得A1B⊥CF.
∠EFC为二面角A—A1B—C的平面角…………………10分
令BC=2,在等腰Rt△ABC中,可求出![]() .
.
在Rt△A1BC中,由BC=2,A1C=2![]() ,求出A1B=2
,求出A1B=2![]() .
.
由FC·A1B=BC·A1C
求出![]() .
.
∠EFC=60°.………………………12分
19. (I)三种电路各自接通分别记为事件A1、A2、A3,则
P(A1)=m3,
P(A2)=1-(1-m)3=3m-3m2+m3,………………4分
P(A3)=2(1-m)m2+m3=2m2-m3. ………………6分
(II)P(A2)-P(A1)=3m-3m2=3m(1-m),
∵0<m<1, ∴P(A2)>P(A1). …………10分
P(A2)-P(A3)=2m3-5m2+3m=m(2m-3)(m-1)>0 ,
∴P(A2)>P(A3).
故三个电子元件并联接通的概率最大,故性能最优. …………12分
20.(I)a1=4000(1-20%)+1000=4000×0.8+1000=4200
a2=(4000×0.8+1000)×0.8+1000=4000×0.82+1000×0.8+1000=4360
a3=4000×0.83+1000×0.82+1000×0.8+1000=4488 …………3分
(II)由(1)猜想an=4000×0.8n+1000×![]() …………5分
…………5分
用数学归纳法证明如下:
①当n=1时,a1=4000×0.81+1000×![]() =4000×0.8+1000,结论正确.
=4000×0.8+1000,结论正确.
②假设n=k时,ak=4000×0.8k+1000×![]() ………………7分
………………7分
则ak+1=ak×0.8+1000=(4000×0.8k+1000×![]() )×0.8+1000
)×0.8+1000
=4000×0.8k+1+1000×![]() +1000
+1000
=4000×0.8k+1+1000×![]()
=4000×0.8k+1+1000×![]() .
.
由①、②知,对任意自然数n,结论正确…………10分
(III)![]()
∴经过若干年后,树木的棵数能大体稳定在5000棵左右. …………12分
21. (I)由题意![]() ,…………2分
,…………2分
设![]() (
(![]() ),由余弦定理, 得
),由余弦定理, 得
![]() .…………4分
.…………4分
又![]() ·
·![]() ,
…………6分
,
…………6分
当且仅当![]() 时,
时,![]() ·
·![]() 取最大值,
取最大值,
此时![]() 取最小值
取最小值![]() ,令
,令![]() ,
,
解得![]() ,
,![]() ,∴
,∴![]() ,
,
故所求![]() 的轨迹方程为
的轨迹方程为![]() . …………8分
. …………8分
(II)设![]() ,
,![]() ,则由
,则由![]() ,可得
,可得![]() ,
,
故![]() . …………10分
. …………10分
∵![]() 、
、![]() 在动点
在动点![]() 的轨迹上,故
的轨迹上,故![]() 且
且![]() ,
,
消去![]() 可得
可得![]() ,解得
,解得![]() ,…………12分
,…………12分
又![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]() .…………14分
.…………14分
22.(Ⅰ)![]() …………2分
…………2分
![]() 上是增函数,在[0,2]上是减函数,
上是增函数,在[0,2]上是减函数,
∴当![]() 取到极大值,
取到极大值,![]() …………4分
…………4分
(Ⅱ)![]()
![]() 的两个根分别为
的两个根分别为![]()
∵函数![]() 上是减函数,
上是减函数,![]() . …………6分
. …………6分
![]() …………8分
…………8分
(Ⅲ)![]() ,
,
![]() …………12分
…………12分
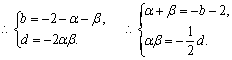
![]()
![]() …………14分
…………14分
