|
2004-2005学年度下学期
高中学生学科素质训练
高三第三轮数学综合测试(2)YCY
说明:本试卷分第一卷和第二卷两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,答题时间120分钟.
参考公式:
三角函数的积化和差公式 正棱台、圆台的侧面积公式
![]()
![]() 其中
其中![]() 、
、![]() 分别
分别
![]() 表示上、下底面周长,
表示上、下底面周长,![]() 表示斜高或母线长
表示斜高或母线长
![]() 球的体积公式
球的体积公式![]()
![]() 其中
其中![]() 表示球的半径
表示球的半径
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.函数![]() 是
( )
是
( )
A.周期为![]() 的奇函数 B.周期为
的奇函数 B.周期为![]() 的偶函数
的偶函数
C.周期为![]() 的奇函数 D.周期为
的奇函数 D.周期为![]() 的偶函数
的偶函数
2.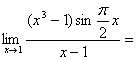 ( )
( )
A.0 B.1 C.2 D.3
3.“0<x<5”是“不等式x-2<3”成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.不充分不必要条件
4.已知-9,a1,a2,-1成等差数列,-9,b1,b2,b3,-1成等比数列,则![]() 等
等
于 ( )
A.±8 B.8 C.-8 D.![]()
5.已知![]() ,则
,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.要从已编号为1—50枚最新研制的某型炮弹中随机抽取5枚进行发射试验,用每部分选
取的号码间隔一样的系统抽样方法确定所抽取的5枚炮弹的编号可能是 ( )
A.5,10,15,20,25 B.3,13,23,33,43
C.1,2,3,4,5 D.2,4,8,16,32
7.已知x、y满足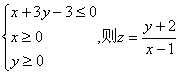 的取值范围是 ( )
的取值范围是 ( )
A.[-2,1] B.![]()
C.[-1,2] D.![]()
8.已知单位正方体ABCD—A1B1C1D1的对棱BB1、DD1上有两个动点E、F,
![]() .设EF与AB所成的角为a,与BC所成的角为b,则a+b的最小
.设EF与AB所成的角为a,与BC所成的角为b,则a+b的最小
值 ( )
A.不存在 B.等于60° C.等于90° D.等于120°
9.不等式![]() <0的解集
( )
<0的解集
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.以抛物线![]() 上任意一点P为圆心作圆与y轴相切,则这些圆必过定点
上任意一点P为圆心作圆与y轴相切,则这些圆必过定点
( )
A.(3,3) B.(4,3) C.(2,3) D.(3,0)
11.已知关于x的方程:![]() 在区间(3,4)内有解,则实数a的取值
在区间(3,4)内有解,则实数a的取值
范围是 ( )
A.![]() B.
B.![]() ) C.
) C.![]() D.
D.![]()
12.某段街道旁边规划树立10块广告牌,广告底色选用红、绿两种颜色,则相邻两块广告
底色不同为绿色的配色方案的种数为 ( )
A.72 B.78 C.144 D.156
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题4小题,每小题4分,共16分。把答案填在题中横线上。
13.在△ABC中,A,B,C成等差数列,则![]() .
.
14.已知![]() 是两个不共线的向量,而
是两个不共线的向量,而![]() 是两个共线
是两个共线
向量,则实数k= .
15.如果双曲线![]() 上一点
上一点![]() 到它的右焦点的距离是8,那么点
到它的右焦点的距离是8,那么点![]() 到它的右准线的距
到它的右准线的距
离是 .
16.对某种产品中的10件不同的正品和2件不同的次品,一一进行测试,到区分出所有次
品为至,若所有次品中恰好在第四次测试中全部出现,则测试的方法有__________种.
三、解答题(本大题共6小题,共74分)本大题共6小题,共74分.解答应写出文字说明,
证明过程或演算步骤.
17.(本小题满分12分)在锐角三角形ABC中,三内角A、B、C的对边分别为a、b、c,
若![]() ,试比较b+c与2a的大小.
,试比较b+c与2a的大小.
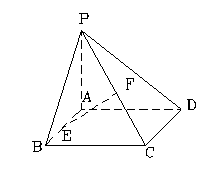
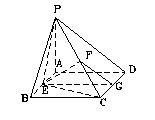
18.(本小题满分12分)在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,
|
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面PAD;
平面PAD;
(Ⅲ)当平面PCD与平面ABCD成多大角时,
直线![]() 平面PCD?
平面PCD?
19.(本小题满分12分)已知函数![]() .
.
(Ⅰ)求反函数;
(Ⅱ)若数列![]() 的前n项和
的前n项和![]() 求数列
求数列![]() 的通
的通
项公式;
(Ⅲ)令![]() ,求
,求![]() .
.
20.(本小题满分12分)某公司取消福利分房和公费医疗,实行年薪制工资结构改革,该公
司从2004年起,每人的工资由三个项目组成,并按下表规定实施:
| 项 目 | 金额(元/年) | 性质与计算方法 |
| 基础工资 | 10000元 | 考虑物价因素,从2005年起每年递增10%(与工龄无关) |
| 房屋补贴 | 400元 | 按职工到公司年限计算,每年递增400元 |
| 医 疗 费 | 1600元 | 固定不变 |
如果该公司今年有5位职工,计划从明年起每年新招5名职工。
(Ⅰ)若2004年算第一年,试把第n年该公司付给职工工资总额y(万元)表示成年限
n的函数;
(Ⅱ)试判断公司每年发给职工工资总额中,房屋补贴和医疗费用的总和能否超过基础
工资总额的20%.
21.(本小题满分12分)如图所示,![]() 是一条曲线段,点
是一条曲线段,点![]() 在直线
在直线![]() 上。点
上。点![]() 到
到![]() 的距离
的距离
等于5,![]() 外一点
外一点![]() 到
到![]() 的距离为2。对于曲线段
的距离为2。对于曲线段![]() 上的任意一点
上的任意一点![]() ,总满足
,总满足![]() ,
,
其中![]() 是点
是点![]() 到直线
到直线![]() 的距离.
的距离.
(Ⅰ)建立适当的坐标系,求出曲线段![]() 的方程;
的方程;
(Ⅱ)设另有一定点![]() ,
,![]() ,
,![]() 、
、![]() 位于
位于![]() 的两侧,且
的两侧,且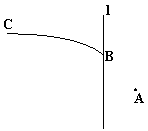 点
点![]() 到
到![]() 的距离为
的距离为![]() ,
,
求曲线段![]() 上的点到点
上的点到点![]() 的最近距离.
的最近距离.
22.(本小题满分14分)已知![]()
(Ⅰ)当![]() 时,
时,![]() 有最小值4,求a的最小值;
有最小值4,求a的最小值;
(Ⅱ)当![]() 时,
时,![]() 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
高三数学(二)参考解答及评分标准
一、选择题:每小题5分,共60分.
(1)A (2)D (3)A (4)C (5)B (6)A
(7)B (8)C (9)A (10)B (11)C (12)C
提示:(2)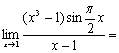
![]() .
.
(5)考查共轭复数的概念.
(7)直线![]() 的斜率
的斜率![]() 的取值范围为所求.
的取值范围为所求.
(8)利用极限思想解题.
二、填空题:每小题4分,共16分.
(13)![]() (14)
(14)![]() 或-2
(15)
或-2
(15)![]() (16)540
(16)540
提示:(14)由![]() ,得
,得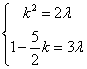 ,可解.
,可解.
三、解答题:
(17) 由![]() ,得
,得![]() .
.
∵DABC是锐角三角形,![]() . …………………………..3分
. …………………………..3分
设DABC外接圆半径为R(R>0),由正弦定理得
![]() ………..9分
………..9分
若B=C,则![]()
|
(18)证(Ⅰ)∵PA^底面ABCD
![]() AD是PD在平面ABCD内的射影。
AD是PD在平面ABCD内的射影。
∵CDÌ平面ABCD,且CD^AD,
故CD^PD .………………...…4分
(Ⅱ)取CD中点G,连结EG、FG
∵E、F分别是AB、PC的中点,\EG//AD,FG//PD,
\平面EFG//平面PAD,\EF//平面PAD. ……………..……8分
(Ⅲ)当平面PCD与平面ABCD成45°角时,直线EF^平面PCD。
证明:G为CD中点,则EG^CD,由(1)知FG^CD,
故ÐEGF为平面PCD 与平面ABCD所成二面角的平面角,即ÐEGF=45°,
从而得ÐADP=45°, AD=AP。
由,得PE=CE。
又F是PC的中点,\EF^PC。
由CD^EG,CD^FG,得CD^平面EFG,CD^EF,即EF^CD,
故EF^平面PCD. …………..……………….………….12分
(19)(Ⅰ) ![]() .…………………………..4分
.…………………………..4分
(Ⅱ) ∵![]()
![]()
则![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列,
的等差数列,
故![]() ,由
,由![]() ,可求得
,可求得![]() .…8分
.…8分
(Ⅲ) ![]() ,
,
则![]() .………….12分
.………….12分
(20) ( I )到第![]() 年该公司共有
年该公司共有![]() 名职工,基础工资总额为
名职工,基础工资总额为![]() 万元,
万元,
房屋补贴总额为: …..2分
![]() 万元, ……….……………………..4分
万元, ……….……………………..4分
医疗费总额为![]() (万元)
(万元)
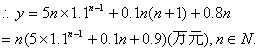 |
…………6分
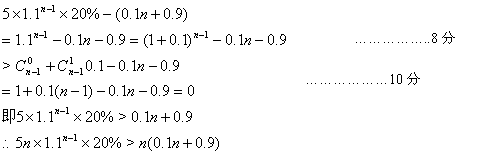 |
(II)
∴每年房屋补贴和医疗费用的总和不会超过基础工资总额20%. …..….12分
(21)(1)以![]() 为
为![]() 轴,且点
轴,且点![]() 在
在![]() 轴的正半轴上建立直角坐标系,则
轴的正半轴上建立直角坐标系,则![]() 的方程为
的方程为![]() ,
,
点![]() 的坐标为
的坐标为![]() ,设点
,设点![]() 是曲线段
是曲线段![]() 上任意一点,则
上任意一点,则
![]() ,
,![]()
![]()
![]() .………..4分
.………..4分
(2)设点![]()
![]() ,点
,点![]() 是曲线段
是曲线段![]() 上任意一点,依题意:
上任意一点,依题意:
![]()
![]()
![]() ,…….6分
,…….6分
若![]() 即
即![]() ,则当
,则当![]() 时,
时,![]() ;………..8分
;………..8分
若![]() 即
即![]() ,则当
,则当![]() 时,
时,![]() ;……….10分
;……….10分
若![]() 即
即![]() ,则当
,则当![]() 时,
时,![]() .………..12分
.………..12分
(22)
(Ⅰ) ![]() ,
……….……2分
,
……….……2分
设 ![]() ,
,
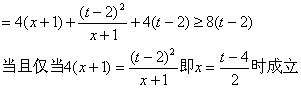
故![]() . ……………….………..6分
. ……………….………..6分
又![]() ,
,
![]() 从而
从而![]()
又![]() ,
,
![]() ,等号在t=4, x=0时取得.….……….8分
,等号在t=4, x=0时取得.….……….8分
(Ⅱ) ![]() 时,
时,
![]()
![]() .
.
若![]() 恒成立,只要
恒成立,只要![]() 恒成立,
恒成立,
即![]() …………………11分
…………………11分
令![]() 则
则![]()
故![]() 当u=1时,
当u=1时,![]() ,
,
即所求t的范围是![]() .…………………………..………….14分
.…………………………..………….14分