|
2004－2005学年度下学期
高中学生学科素质训练
高三第三轮数学综合测试（3）
YCY
说明：本试卷分第一卷和第二卷两部分.第Ⅰ卷60分，第Ⅱ卷90分，共150分，答题时间120分钟.
参考公式:
三角函数的积化和差公式 正棱台、圆台的侧面积公式
其中
、
分别
表示上、下底面周长,
表示斜高或母线长
球的体积公式
其中
表示球的半径
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有
一项是符合题目要求的.
1．设p、q为简单命题，则“p且q”为假是“p或q”为假的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
2．下列四个函数中，同时具有性质：①最小正周期为2p；②图象关于直线x=
对称的一个函数是 （ ）
A．y=sin(x－
) B．y=sin(x+) C．y=sin(x+) D．y=sin(2x－)
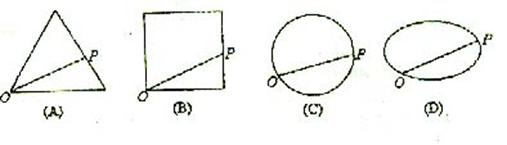
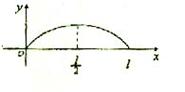3．点P从O 点出发，按逆时针方向沿周长为的图形运动一周，O、P两点连线的距离y与点P走过的路x的函数关系如右图，那么点P所走的图形是
（ ）
4．在复平面内，设向量
=(x1,y1)，
=(x2,y2)，设复数z1=x1+y1i；z2=x2+y2i
(x1,x2,y1,y2∈R)，则•等于 （ ）
A．
z2+z1
B．z2－z1 C．
(z2－z1) D．(z2+z1)
5. 已知函数y=f(x)对任意实数都有f(-x)=f(x),f(x)=-f(x+1)且在［０，１］上单调递减，则 （ ）
A．ｆ（
）＜ｆ（
）＜ｆ（
） B．ｆ（）＜ｆ（）＜ｆ（）
C．ｆ（）＜ｆ（）＜ｆ（） D．ｆ（）＜ｆ（）＜ｆ（）
6．双曲线
的一条准线被它的两条渐近线所截得线段长度恰好为它的一个焦点
到一条渐近线的距离，则该双曲线的离心率是 （ ）
A．3 B．2
C．
D．
7．若一个圆的圆心在抛物线y2=4x的焦点处，且此圆与直线x+y+1=0相切，则这个圆的方程是 （ ）
A．x2+y2－2x－1=0 B．x2+y2+2x+1=0
C．x2+y2－2y+1=0 D．x2+y2+2y+1=0
8．如果f(a+b)=f(a)•f(b)且f(1)=2，则
+
+
+…+
等于 （ ）
A．2003 B．1001 C．2004 D．2002
9．计算机将信息转换成二进制进行处理，二进制即“逢2进1”，如（1101）2表示二进数，将它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数
转换成十进制形式是 （ ）
A．217－2 B．218－2 C．218－1 D．217－1
10．棱长为2的正方体ABCD—A1B1C1D1中，E、F分别是棱AB、BC的中点，则点C1到平面B1EF的距离为 （ ）
A．
B．
C．
D．
11．某种产品有4只次品和6只正品，每只产品均不相同且可区分，今每次取出一只测试，直到4只次品全测出为止，则最后一只次品恰好在第五次测试时，被发现的不同情况种数是 （ ）
A．24 B．144 C．576 D．720
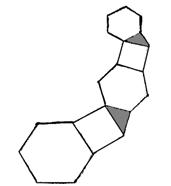12．以边长为1的正六边形的一边为边向外作正方形，以正方形的一边为底向外作等腰直角三角形，再以等腰直角三角形一条直角边为边向外作正六边形，……，如此继续无限反复同一过程，则这些正六边形、正方形、等腰直角三角形面积之和为
（ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分．
13．在数列
中，
，且对任意大于1的正整数
，点
在直线
上，则
_____________．
14．已知
的展开式中所有二项式系数的和为512，则展开式中
项的系数为_ ____．
15．在
中，有命题①
；②
；③若
，则为等腰三角形；④若
，则为锐角三角形.上述命题正确的是_____________ ．
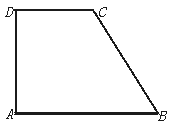
16．已知四个面都是直角三角形的三棱锥，其中三个面展开后构成一直角梯形ABCD，如图，AD⊥AB，AD⊥DC，AB=2，BC=
，CD=1，则这个三棱锥外接球的表面积是__________（结果可含π）.
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分12分）
已知
、
是
的两个内角，且
、
是方程
的两个实根，求
的取值范围．
18．（本小题满分12分）
口袋里装有大小相同的卡片八张，其中三张标有数字1，三张标有数字2，二张标
有数字3，第一次从口袋里任里任意抽取一张，放回口袋里后第二次再任意抽取一张，
记第一次与第二次取到卡片上数字之和为
．
（1）为何值时，其发生的概率最大？说明理由；
（2）求随机变量的期望E．
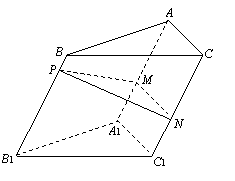
19．(本题满分12分) 如图，点
为斜三棱柱
的侧棱
上一点，
交
于点
，
交
于点
．
（1）求证：
；
（2）在任意
中有余弦定理：
. 拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并予以证明．
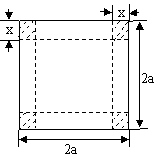
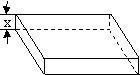
20．(本题满分12分)从边长2a的正方形铁片的四个角各截一个边长为x的正方形，然后拆
成一个无盖的长方体盒子，要求长方体的高度x与底面正方形边长的比不超过正常数t．
（1）把铁盒的容积V表示为x的函数，并指出其定义域；
（2）x为何值时，容积V有最大值．
21．(本小题满分12分)
已知函数f(x)=
(3x－b)的图象过点A（1，2），B（2，5）
（1）求函数f－1(x)的解析式；
（2）记an=
,n∈N*,是否存在正数k,使得（1+
）(1+
)…(1+
)≥k
对
一切n∈N*均成立，若存在求出k的最大值，若不存在说明理由。
22．（本小题满分14分）
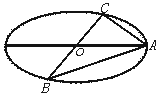
已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的一个顶点，BC过椭圆
中心O，如图，且
·
=0，BC=2AC，
（1）求椭圆的方程；
（2）如果椭圆上两点P、Q使∠PCQ的平分线垂直AO，则总存在实数λ,使
=λ
,
请给出证明．0
高三数学（三）参考解答及评分标准
一、选择题：每小题5分，共60分.
（1）B （2）B （3）D （4）D （5）B （6）B
（7）A （8）C （9）C （10）B （11）C （12）C
提示：
4．
＝
＝
＝
．
8．
．
9．等比数列求和．
二、填空题：每小题4分，共16分.
（13）3
（14）-84
（15）②，③
（16）
提示：
13．由题意
，
是首项为
，公差为的等差数列．
16．取
的中点
，连结
，
；得三棱锥外接球的半径为
．
三、解答题：
17．依题意有，＋＝
，＝
，
＝
＝
＝1．…………..3分
，
．从而
，
，
故
，．…………..6分
即方程的两个实根均在
内．
设
，
则函数
与
轴有两个交点，且交点在内；
又函数的图象是开口向上的抛物线，且对称轴方程为
，
故其图象满足
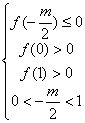即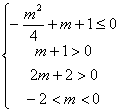
…………..9分
解之，得
，
故所求的范围是
．…………..12分
18．（１）依题意，随机变量的取值是2、3、4、5、6．…………2分
因为P（=2）=
；P（=3）=
，
P（=4）=
；P（=5）=
；
P（=6）=
；…………7分
所以，当=4时，其发生的概率P（=4）=
最大．…………8分
（Ⅱ）E=
．………………12分
19．(1)
；
(2) 在斜三棱柱
中，有
，其中
为平面
与平面
所组成的二面角.
上述的二面角为
,在
中，
，
由于
，
有.
20．（１）V=4(a－x)2•x，定义域为(0,
)；
（２）当t≥
时，x=
，V取最大值；当0<t<时，x=，V取最大值．
21．(1)由已知得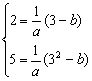
解得
…………2分
∴f(x)=
(3x+1)
…………4分
令y=f(x),由y= (3x+1)得3x=2y-1,∴x=log3(2y-1)，
∴f-1(x)=log3(2x-1)(x>)．
…………6分
(2)an=3log3(2n-1)=2n-1,n∈N* …………8分
设存在正数k，使（1+）(1+)…(1+)≥k成立，
则k≤
,
记F(n)= ,则
F(n+1)= 
,
∴F(n+1)>F(n)，
∴F(n)是随n的增大而增大， …………10分
∵n∈N*,∴当n=1时，F（n）min=F(1)=
,
∴k≤,即k的最大值为.
…………12分
22．（1）以O为原点，OA所在的直线为x轴建立如图所示的直角坐标系，
则A（2，0），设所求椭圆的方程为：
=1(0<b<2),由椭圆的对称性知OC=OB,
由·=0得AC⊥BC，
∵BC=2AC，∴OC=AC，∴△AOC是等腰直角三角形，∴C的坐标为（1，1），
∵C点在椭圆上
∴
=1,∴b2=
,所求的椭圆方程为
=1．
…………6分
（2）由于∠PCQ的平分线垂直OA（即垂直于x轴），不妨设直线PC的斜率为k，则直线QC的斜率为-k，直线PC的方程为：y=k(x-1)+1,直线QC的方程为y=-k(x-1)+1, ………………8分
由
得：(1+3k2)x2-6k(k-1)x+3k2-6k-1=0（*） …………10分
∵点C（1，1）在椭圆上，∴x=1是方程（*）的一个根，则其另一根为
,设P（xP,yP）,Q(xQ,yQ),xP=,
同理xQ=
,
…………12分
kPQ=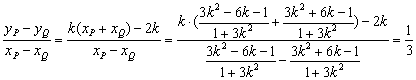
而由对称性知B(-1,-1),又A（2，0），
∴kAB=
，
∴kPQ=kAB，∴与共线，且≠0,即存在实数λ，使=λ. ………14分