|
2004－2005学年度下学期
高中学生学科素质训练
高三第三轮数学综合测试（4）
YCY
说明：本试卷分第一卷和第二卷两部分.第Ⅰ卷60分，第Ⅱ卷90分，共150分，答题时间120分钟.
参考公式:
三角函数的积化和差公式 正棱台、圆台的侧面积公式
其中
、
分别
表示上、下底面周长,
表示斜高或母线长
球的体积公式
其中
表示球的半径
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有
一项是符合题目要求的.
1．设
、
是两个非空集合，定义：
.若
，则
中元素的个数是 （ ）
A．3 B．4 C．7 D．12
2．双曲线
的焦点到渐近线的距离为 （ ）
A．2 B．3 C．4 D．5
3．
为等差数列，且
…
，则此数列的前15项之和
等于（ ）
A．146 B．150 C．165 D．180
4．若
，则下列
，
的关系中不能成立的是（ ）
A．
B．
C．
D．
5．在正四面体的一个顶点处，有一只蚂蚁每一次都以
的概率从一个顶点爬到另一个顶点。那么它爬行了4次又回到起点的概率是 （ ）
A．
B．
C．
D．
6．已知圆
,点
,其中
,
是圆
上的动点,
的中
垂线交
所在直线于,则点的轨迹是 （ ）
A．椭圆 B．双曲线 C．抛物线 D．直线
7．设
则
的值等于 （ ）
A．－
B．－
C． D．
8．将边长为
的正方形
沿对角线
折起，使得
，则二面角
的正切值等于 （ ）
A．
B．
C．
D．
9．某城市对一种售价为每件160元的电子产品征收附加税，税率为
（即每销售100元征税元），若年销售量为30－
万件，要使附加税不少于128万元，则R的取值范围是 （ ）
A．[4，8] B．[6，10] C．[4%，8%] D．[6%，10%]
10．图中的每个开关都有闭合与不闭合两种可能,电路从
到接通的情况共有（ ）种．
A．30 B．24
C．16 D．12
11．已知向量
夹角为
若
，则的值为（ ）
A．
B．
C．
D．
12．已知
的图象经过点
，且
.记
（其中
是两个不相等的正实数），则
的大小关系是 （ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分.
13．关于x的不等式
的解集是
，则关于
的不等式
的解集为 ．
14．已知
的展开式的第7项为
，
的值
为 ．
15．已知正态总体落在区间（
）里的概率是
，那么相应的正态曲线
在＝
________时，达到最高点.
16．有如下四个命题：
①若两条直线在一个平面内的射影是两条平行直线，则这两条直线也平行；
②平面
和平面
垂直的充要条件是平面内有一条直线与平面垂直；
③平面和平面平行的一个必要不充分条件是内有无数条直线与平面平行；
④直线与平面平行的一个充分不必要条件是平面内有一条直线与直线平行。
其中正确的序号是 ．
三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.
17．（本小题满分12分）
如图，在三棱椎P—ABC中△ABC是正三角形，∠PCA=90º，D是PA的中点，二
面角P—AC—B为120º，PC=2，
．
（1）求证：AC⊥BD；
（2）求BD与底面ABC所成角的正弦值．
18．（本小题满分12分）
△ABC中，复数
，
．
（1）问
是否为定值；
（2）当∠C为最大时，存在动点M使MA，AB，MB成等差数列，试求
的最大值．
19．（本小题满分12分）
在中国轻纺城批发市场，季节性服装当季节即将来临时，价格呈上涨趋势。设某服装开始时定价为10元，并且每过一周（7天）涨价2元，5周后开始保持20元的价格平稳销售；10周后当季节即将过去时，平均每周削价2元，直道16周末，该服装已不再销售．
（1）试建立价格与周次
之间的函数关系；
（2）若此服装每件进价与周次之间的关系为
，
试问该服装第几周每件销售利润
最大？
20．（本小题满分12分）
已知函数满足
，且
．
（1）当
时，求的表达式；
（2）设
,求证：
；
（3）设
，，
，
求
．
21．（本小题满分12分）
已知椭圆的中心在原点，焦点在y轴上，离心率
，焦点到相应准线的距离为
．
（1）求该椭圆的方程；
（2）P、Q是椭圆上的点，上焦点F在线段PQ上，且有
，求P、Q所在直
线的方程．
22．（本小题满分14分）
已知函数
．
（1）函数的图象关于原点对称的充要条件是什么？证明你的结论；
（2）对于满足（1）的函数，解关于x的不等式
；
（3）证明：当
，且
时，
．
高三数学（四）参考解答及评分标准
一、选择题：每小题5分，共60分.
1－5 D A C A B
6－10 B D C A C
11－12 C B
提示：
3．由已知得
，
．
5．由题意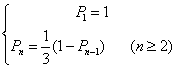
12．
为“上凸”的函数．
二、填空题：每小题4分，共16分.
13、
． 14、
． 15、0.2 ． 16、②③．
提示：
14．由题意可得
．
三、解答题
17、（1）取AC的中点E，连结DE、BE，则DE∥PC。∵PC⊥AC，∴AC⊥DE，又AC⊥BE，∴AC⊥平面BDE，∴AC⊥BD．……5.分
（2）∵AC⊥平面BDE，∴平面BDE⊥平面ABC∴BE是BD在底面ABC上的射影 ∴∠DBE为BD与底面ABC所成的角．….8分
又∵DE⊥AC，BE⊥AC，∴∠BED是二面角P-AC-B的平面角，即∠BED=120°，在△BDE中，由正弦定理得
……12分
18. （1）由
，得
，即
∴=
（定值）……………….5分
（2）
……8分
当且仅当
时，
最大．
设
，由
知，动点M在以AB为焦点的圆上，
以AB的中点为原点，直线AB为x轴建立直角坐标系，则椭圆方程为
．
设M（x，y），则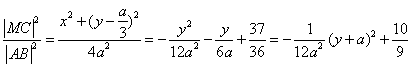
，
∴当
时，
取最大值
．…….12分
19．（1）
8+2t 
P = 20 
…………………..6分
40-2t 
(2)因每件销售利润=售价—进价=P—Q，所以
当时，
，则t=5时，L取最大值7.125
当时，
，则t=6或10时L取最大值8.5
当时，
，则t=11时L取最大值7.125
以上t的取值均为大于0的自然数，因此该服装第6周或第10周每件销售利润最大．….12分
20、（1）由已知得f (n)=f (n -1) f (1)=
f (n-1)=
f (n-2)=…=
；….4分
（2）由（1）知
，设
，则用错位相减法求和得：
；……..9分
（3）∵
∴ 
= 4
= 4．……………….12分
21、（1）设椭圆方程为
．
依题意得方程组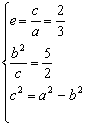
解得，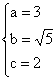
得椭圆的方程为
.……….6分
（2）如图，不妨设P点在Q点的左方且P、Q在准线上的射影分别为
、
，
∵｜QF｜＝2｜PF｜，设｜PF｜＝k，则｜QF｜＝2k.
由
，
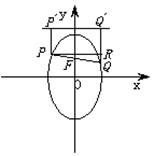得到
.
过P作PR⊥
，则
.
又有
.
在
中，
.
∴
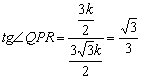，即∠QPR＝
.
则P、Q所在的直线的斜率为
. 由F（0,2）即得过P、Q的直线方程为
. 当P点在Q点的右方时，则所求的直线方程为
．….12分
22．（1）
的定义域是
，
的图象关于原点对称
不恒为0）…5分
（2）由
，得
∵
，
∴
∵
，∴
．
当
≥1时，不等式
解集为
；
当≤－1时，不等式为R；
当
时，
..10分
（3）
，当
≥3时，
…
， ∴
．
………………..14分