|
2004-2005学年度下学期
高中学生学科素质训练
高三第三轮数学综合测试(5)
YCY
说明:本试卷分第一卷和第二卷两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,答题时间120分钟.
参考公式:
三角函数的积化和差公式 正棱台、圆台的侧面积公式
![]()
![]() 其中
其中![]() 、
、![]() 分别
分别
![]() 表示上、下底面周长,
表示上、下底面周长,![]() 表示斜高或母线长
表示斜高或母线长
![]() 球的体积公式
球的体积公式![]()
![]() 其中
其中![]() 表示球的半径
表示球的半径
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.设集合![]() ,在图中能表示从集合
,在图中能表示从集合![]() 到集合
到集合![]() 的映射的是
的映射的是
 ( )
( )
2.要完成下列2项调查:①从某社区125户高收入家庭,280户中等收入家庭,95户低收入家庭中选出100户调查社会购买力的某项指标;②从某中学高一年级的12名体育特长生中选出3人调查学习负担情况. 应采用的抽样方法是 ( )
A.①用随机抽样法 ②用系统抽样法 B.①用分层抽样法 ②用随机抽样法
C.①用系统抽样法 ②用分层抽样法 D.①、②都用分层抽样法
3.已知![]() 则y与x的函数关系式为( )
则y与x的函数关系式为( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
4.已知命题![]() :函数
:函数![]() 的值域为
的值域为![]() ,命题
,命题![]() :函数
:函数![]() 是
是
减函数,若![]() 或
或![]() 为真命题,
为真命题,![]() 且
且![]() 为假命题,则实数
为假命题,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]() 或
或![]()
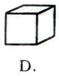
5.下图代表未折叠正方体的展开图,将其折叠起来,变成正方体后,图形是 ( )
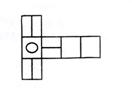

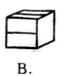
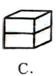
6.直线l是双曲线![]() 的右准线,以原点为圆心且过双曲线的焦点的圆被直线l分成弧长为2比1的两段圆弧,则该双曲线的离心率是 ( )
的右准线,以原点为圆心且过双曲线的焦点的圆被直线l分成弧长为2比1的两段圆弧,则该双曲线的离心率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
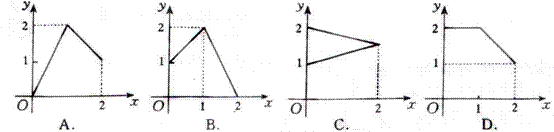
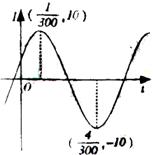 7.电流强度
7.电流强度![]() (安培)随时间
(安培)随时间![]() 变化的函数
变化的函数![]() 的
的
图像如图所示,则当![]() (秒)时的电流强度是( )
(秒)时的电流强度是( )
A.0安培 B.10安培
C.10安培 D.5安培
8.![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知函数![]() =
=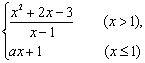 在点
在点![]() 处连续,则
处连续,则![]() 的值是 ( )
的值是 ( )
A.2 B.3 C.-2 D.-4
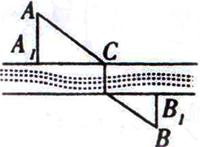
10.在宽2公里的河两岸有![]() 两个城市,它们的直线距离为10公里,
两个城市,它们的直线距离为10公里,![]() 城到河岸的垂直距离
城到河岸的垂直距离![]() 公里,
公里,![]() 城到河岸的垂直距离
城到河岸的垂直距离![]() 公里,现要选址建桥,使得从
公里,现要选址建桥,使得从![]() 到
到![]() 的路程最短,则最短路程为(河两岸近似看作两条平行直线) ( )
的路程最短,则最短路程为(河两岸近似看作两条平行直线) ( )
 A.10公里 B.
A.10公里 B.![]() 公里
公里
C.![]() 公里 D.
公里 D.![]() 公里
公里
11.以双曲线![]() 的右焦点为顶点,左顶点为焦点的抛物线的方程是
( )
的右焦点为顶点,左顶点为焦点的抛物线的方程是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.点P的曲线![]() 上移动,在点P处的切线的倾斜角为α,则α的取值范围是( )
上移动,在点P处的切线的倾斜角为α,则α的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
二、填空题:(本大题共4小题,每小题4分,共16分.)
13.若![]() ,则
,则![]() =__________
_.
=__________
_.
14.海面上,地球球心角1′所对的大圆弧长约为1海里,在赤道上,东经140°与西经130°的海面上有两点A、B。则A、B两点的球面距离是_____ ___海里.
15.对曲线离心率![]() 等于
等于![]() (其中
(其中![]()
![]()
![]() 、
、![]()
![]()
![]() )的不同形状的双曲线个数为____________ .
)的不同形状的双曲线个数为____________ .
![]()
16.函数![]()
![]() 满足
满足![]() 是偶函数,又
是偶函数,又![]() ,
,![]() 为奇函数则
为奇函数则![]() ________ __.
________ __.
三、解答题:(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分12分)
在一次环保知识竞赛中,有6道选择题和2道判断题放在一起供抽取,每支代表队
要抽3次,每次只抽一道题回答.
(1)不放回的抽取试题,求只在第三次抽到判断题的概率;
(2)有放回的抽取试题,求在三次抽取中抽到判断题的个数![]() 的概率分布及
的概率分布及![]() 的期望.
的期望.
18.(本小题满分12分)
设函数![]() ,
,![]() ,
,![]() ;
;
(1)若![]() 在
在![]() 上是增函数,求
上是增函数,求![]() 的取值范围;
的取值范围;
(2)求![]() 在
在![]() 上的最大值.
上的最大值.
19.(本小题满分12分)
如右图所示,点![]() 分别是正方体
分别是正方体![]() 上
上
的点.
(1)若![]() ,求证:无论点
,求证:无论点![]() 在
在![]() 上如何移动总有
上如何移动总有![]() 丄
丄![]() ;
;
(2)若![]() 且
且![]() 丄平面
丄平面![]() ,求二面角
,求二面角![]() 的大小;
的大小;
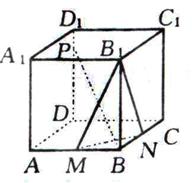 (3)棱
(3)棱![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得平面
,使得平面![]() 丄平面
丄平面![]() ?证明你的结论.
?证明你的结论.
20.(本小题满分12分)
设一次函数![]() 的图像关于直线
的图像关于直线![]() 对称的图象为
对称的图象为![]() ,且
,且![]() ,若点
,若点
![]()
![]() 在曲线
在曲线![]() 上,并有
上,并有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() 的值.
的值.
21.(本小题满分12分)
如图所示,平地上有一条水沟,沟沿是两条长100![]() 的平行线段,沟宽
的平行线段,沟宽![]() 为2
为2![]() ,
,
与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为![]() ,对称轴与地面垂直,
,对称轴与地面垂直,
沟深![]() ,沟中水深1
,沟中水深1![]() .
.
(1)求水面的宽;
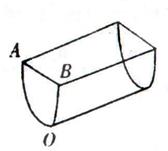 (2)现要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,问改挖后的沟底宽为多少米时,所挖的土最少?
(2)现要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,问改挖后的沟底宽为多少米时,所挖的土最少?
22.(本小题满分14分)
已知在平面直角坐标系![]() 中,向量
中,向量![]() ,
,![]() 的面积为
的面积为![]() ,且
,且
![]() ,
,![]() .
.
(1)设4<![]() <
<![]() ,求向量
,求向量![]() 与
与![]() 的夹角
的夹角![]() 的取值范围;
的取值范围;
(2)设以原点![]() 为中心,对称轴在坐标轴上,以
为中心,对称轴在坐标轴上,以![]() 为右焦点的椭圆经过点
为右焦点的椭圆经过点![]() ,且
,且
![]()
![]() ,当
,当![]() 取最小值时,求椭圆的方程.
取最小值时,求椭圆的方程.
高三数学(五)参考解答及评分标准
一、选择题:每小题5分,共60分.
(1)D (2)B (3)C (4)D (5)B (6)D
(7)A (8)A (9)B (10)B (11)B (12)B
提示:
1.考查映射的概念 3.注意定义域 4.![]() 真
真![]() 假或
假或![]() 假
假![]() 真
真
9.根据![]() 可解
可解
二、填空题:每小题4分,共16分.
(13)2101
(14)5400海里
(15)![]() (16)2003
(16)2003
提示:16.![]() 为周期函数,周期为4
为周期函数,周期为4
三、解答题:
17、(1)若不放回抽取三道试题有![]() 种方法,只在第三次抽到判断题有
种方法,只在第三次抽到判断题有![]() 种方法。
种方法。
则只在第三次抽到判断题的概率![]() .…………4分
.…………4分
(2)若有放回的抽取试题,每次抽取到的判断题概率为![]() ,且相互独立。所以在三次抽取中抽到判断题的个数
,且相互独立。所以在三次抽取中抽到判断题的个数![]() 的概率分布为:
的概率分布为:
![]()
![]()
![]()
![]() ………8分
………8分
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
…………10分
![]() ~
~![]() …………12分
…………12分
18. 解:当![]() 时,
时,![]()
(1)要使![]() 在
在![]() 上是增函数,
上是增函数,![]()
![]() 在
在![]() 上恒成立。
上恒成立。
即![]() 在
在![]() 上恒成立。
上恒成立。
而![]() 在
在![]() 上的最小值为
上的最小值为![]() ,又
,又![]()
![]()
![]() …………6分
…………6分
(2)ⅰ)![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
![]() …………8分
…………8分
ⅱ)![]() 时,
时,![]() ,得
,得![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]()
![]() …………12分
…………12分
19、(1)证![]() 丄平面
丄平面![]() ;……4分 (2)所求角的大小为
;……4分 (2)所求角的大小为![]() ;……8分
;……8分
(3)存在点P,且P为![]() 的中点,使得平面
的中点,使得平面![]() 丄平面
丄平面![]() ,先证明
,先证明![]() 丄平面
丄平面![]() ,再取
,再取![]() 中点E,连结
中点E,连结![]() ,有
,有![]() ∥
∥![]() ,从而
,从而![]() 丄平面
丄平面![]() ,故结论成立. …12分
,故结论成立. …12分
20.(1)设![]() .
.
由![]()
![]() . ①
. ①
![]() ,在曲线
,在曲线![]() 上,
上,
![]()
![]() ②
②
由①②得![]() 故曲线
故曲线![]() 的方程为
的方程为![]() …………5分
…………5分
由点![]() .于是
.于是
![]() .
.
即![]()
![]() …………8分
…………8分
(2)![]()
![]()
![]()
![]()
![]()
![]() …………12分
…………12分
21.(1)建立直角坐标系,设抛物线的方程为![]()
![]() .
.
于是抛物线的方程为![]() .
.![]() .……4分
.……4分
(2)设![]()
![]()
![]() ,
,
即![]() .于是,
.于是,![]()
![]()
![]() …………8分
…………8分
令![]() .…………10分
.…………10分
![]() S最小,此时所挖土最少,这时
S最小,此时所挖土最少,这时![]() 因此,当
因此,当![]() 时,所挖土最少。…………12分
时,所挖土最少。…………12分
22、
(1)由![]() ,由
,由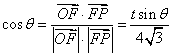 ,得
,得![]() .…………3分
.…………3分
![]() 4<
4<![]() <
<![]()
![]()
![]()
![]() 夹角
夹角![]() 的取值范围是
的取值范围是![]() .…………6分
.…………6分
(2)设![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …………10分
…………10分
![]()
![]()
椭圆长轴![]()
![]()
故所求椭圆方程为![]() .…………14分
.…………14分