2002-2003学年度上学期
高中学生学科素质训练
高三数学测试题—数列、数学归纳法(7)
一、选择题(本题每小题5分,共50分)
1.数列{an}中,已知![]() 等于( )
等于( )
A.33 B.21 C.17 D.10
2.数列{an}中,![]() 等于 ( )
等于 ( )
A.163 B.164 C.165 D.166
3.已知![]() 是各项均为正数的等比数列,且公比q≠1,则A=
是各项均为正数的等比数列,且公比q≠1,则A=![]() B=
B=![]() 的大小关系是 ( )
的大小关系是 ( )
A.A>B B.A<B
C.A=B D.不确定,由公比q的取值而定
4.等差数列的前10项之和是前5项之和的4倍,则它的首项a1与公差d的比![]() =( )
=( )
A.![]() B.2 C.
B.2 C.![]() D.4
D.4
5.设{an}是公差为2的等差数列,![]() 等于 ( )
等于 ( )
A.-50 B.50 C.16 D.82
6.在等比数列{an}中,已知![]() ( )
( )
A.44 B.45 C.46 D.47
7.在50—350之间所有个位数字是1的整数之和是 ( )
A.5880 B.5339 C.5208 D.4877
8.若![]() 的前n项和是 ( )
的前n项和是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.均不为0的三个复数![]() 成等比数列,则下列结论中正确的是( )
成等比数列,则下列结论中正确的是( )
A.它们的辐角主值成等差数列
B.它们的模成等比数列
C.它们的模成等比数列且辐秀主值成等差数列
D.以上都不正确
10.数列{an}的前n项和为Sn,P为常数,且满足![]() ,
,
又已知![]() ( )
( )
A.2 B.1 C.![]() D.不确定
D.不确定
二、填空题(本题11—14小题每题4分,15—16小题每题5分,共26分)
11.在等差数列{an}中,它的前n项和为Sn,已知![]() .
.
12.在等差数列{an}中,![]() 最大时,n的值是
.
最大时,n的值是
.
13.在等差数列{an}中,![]() 恰等于这个数列中连续5项之和,这连续的5项是
.
恰等于这个数列中连续5项之和,这连续的5项是
.
14.在等差数列{an}中,它的前n项和记为Sn,已知![]() ,
,
则n的值是 .
15.在无穷递缩等比数列{an}中,已![]()
则![]() .
.
16.在等差数列{an}中,已知公差d=5,前20项的和![]()
![]()
.
三、解答题
17.(本题满分12分)
数列{an}的前n项和为![]() 若将此数列按如下规律编组:
若将此数列按如下规律编组:![]()
……,求第n组的n个数之和.
18.(本题满分12分)
在△ABC中,a、b、c分别是内角A、B、C的对边,已知![]() 、b2、c2成等差数列,求证:ctgA、ctgB、ctgC也成等差数列.
、b2、c2成等差数列,求证:ctgA、ctgB、ctgC也成等差数列.
19.(本题满分12分)
在平面上有n个圆,任两个圆都相交于两个交点,任三个圆不交于同一点,记这n个圆把平面分成的区域个数为![]() ,
,![]() 、f(2)、f(3)、f(4),猜想f(n)的表达式,并证明它.
、f(2)、f(3)、f(4),猜想f(n)的表达式,并证明它.
20.(本题满分12分)
已知![]() 成等比差数列(n为正偶数).又
成等比差数列(n为正偶数).又![]() 的3的大小.
的3的大小.
21.(本题满分12分)
已知数列{an}的首项![]() 是以p为公比的等比数列. {an}的前n项和为
是以p为公比的等比数列. {an}的前n项和为![]()
(1)试问:S1,S2,S3……,Sn,……能否构成等差数列或等比数列,给出证明;
(2)设![]()
22.(本题满分14分)
数列{an}的前n项和为![]()
(1)求通项an;
(2)是否存在常数a、b,使得对一切自然数n都有![]() 成立.若存在,求
成立.若存在,求
出a、b的值;若不存在,说明理由.
高三数学测试题参考答案
七、数列、数学归纳法
一、选择题
1.A 2.D 3.A 4.A 5.D 6.C 7.A 8.A 9.B 10.A
二、填空题
11.18;12.n=6或n=7; 13.![]() ; 14.n=15; 15.-2;16.2000
; 14.n=15; 15.-2;16.2000
三、计算题
17.解:由![]()
由于n=1也成立,![]() 分组是(5),(9,13),(17,21,25),……,
分组是(5),(9,13),(17,21,25),……,
设{an}:5,9,13,…,所求第n组中n个数的和应为
![]()
![]()
18.解:![]() 、b2、c2成等差数列,故
、b2、c2成等差数列,故![]()
![]()
![]()
![]() 、ctgB、ctgC成等差数列.
、ctgB、ctgC成等差数列.
19.解:一个圆把平面分成两部分,![]() 两个相交的圆把平面分成4部分,
两个相交的圆把平面分成4部分,
![]() ,下面用数学归纳法给出证明:
,下面用数学归纳法给出证明:
![]() 一个圆把平面分成2个部分,猜想成立.
一个圆把平面分成2个部分,猜想成立.
2°假设当n=k时,k个圆把平面分成f(k)=k2-k+2个部分,那么当n=k+1时,平面上有k+1个圆,任取其中一个圆记作Ck+1,其余的k个圆由归纳假设知,把平面分成f(k)=k2-k+2个部分.由于任两个圆都有两个交点,任三个圆不交于同一点,所以圆Ck+1与其余k个圆相交的交点数为2k,这2k个交点把圆Ck+1分成2k段弧,每段弧都把原来的平面区域一分为二,这样共增加了2k个平面区域.这时k+1个圆把平面分成的区域就是f(k+1)=(k2-k+2)+2k=k2+k+2=(k+1)2-(k+1)+2.这就是说,当n=k+1时,猜想也成立.
由1°、2°可知,对一切自然数n,满足题目条件的n个圆把平面分成的区域数为
f(n)=n2-n+2.
20.设等差数列{an}的公差为d,及f(1)=n2,f(-1)=n,得![]()
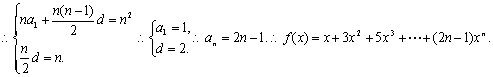
![]()
二式相减得:![]()
![]()
21.①![]() 时an是以P为公比的等比数列,
时an是以P为公比的等比数列,![]()
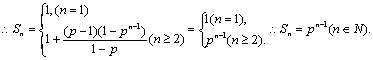
又![]() 能构成等比数列,但不能构成等差数列.
能构成等比数列,但不能构成等差数列.
②![]()
![]()
![]()
![]()
22.①![]()
②假设存在这样的a,b,使得对一切自然数n都有![]()
则![]()
令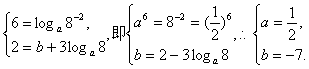 ∴存在这样的数
∴存在这样的数![]()