2002－2003学年度上学期
高中学生学科素质训练
高三数学测试题—复数（8）
一、选择题（本题每小题5分，共50分）
1．若复数
是虚数，则 （ ）
A．
B．
C．
D．
2．设
的主辐角主值是 （ ）
A．
B．
C．
D．
3．已知
的一个必要但不充分的条件是 （ ）
A．
B．
C．
D．
4．已知复数
的模等于 （ ）
A．
B．
C．
D．
5．已知
（ ）
A．
B．
C．
D．
6．设复数
，则函数
的性质适合（ ）
A．最小正周期为π，值域为
B．最小正周期为π，值域为
C．最小正周期为
值域为
] D．最小正周期为值域为
7．复平面上的点z对应复数z=a+bi，（a,b∈R），
是z的共轭复数，下列命题
①若z=1，则
； ②
是纯虚数；
③若点Z在第二象限，则
其中正确的是 （ ）
A．① B．② C．③ D．①②③
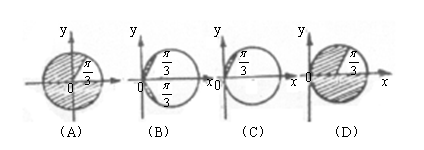
8．
，则z在复平面内表示的点集是图（ ）中的
阴影部分.
9．设
的根是 （ ）
A．4个 B．2个 C．3个 D．1个
10．在复平面上有三个村庄A（0，1），B（
），O（0，0）（单位：公里），现要建一个自来水厂向这三个村庄供水，适当选取厂址可节约供水管道，则最少需要铺设管道的公里数是 （ ）
A．
B．
C．2
D．
二、填空题（本题11—14小题每小题4分，15—16小题每小题5分，共26分）
11．集合
是
.
12．复数
的辐角主值是
.
13．若
的三角形式是 .
14．
.
15．设
，则m的最大值是
.
16．若
的值是
.
三、解答题
17．（本题满分12分）
若、
、b可否比较大小？若不可，说明理由；若可，指明大小关系，并证明你的结论.
18．（本题满分12分）
已知常数
，又复数z满足
，求复平面内z对应的点的轨迹.
19．（本题满分12分）
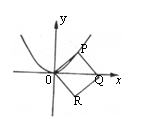如图，设P是抛物线
上任意一点，以线段OP为一边作正方形OPQR（O、P、Q、R按顺时针顺序排列），利用复数求点R的轨迹.
20．（本题满分12分）
已知、
、2、
成
等差数列，求
的最大值.
21．（本题满分12分）
设z为复数，在复平面上已知曲线C1、C2、C3且C1满足
，C2满足
C3满足
C1与C3的两个公共点为A、B，分别过A、B作x轴的平行线交C2于M、N两点，OM、ON的倾角分别为α、β，（O为原点）求cos(α+β)的值.
22．（本题满分4分）
复平面内曲线C的方程是
，Z1、Z2、Z3是曲线C上的点，点Z1所对应的复数是
，试确定三角形Z1Z2Z3的个数.
高三数学测试题参考答案--八、复数
一、选择题
1．D 2．C 3．A 4．C 5．D 6．D 7．A 8．C 9．C 10. B
|
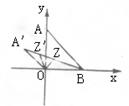
（公里）其中
，等号成立当且仅当z，
同向共线，即∠AZB=∠BZO=∠OZA=120°时，d有最小值公里，图示为
A′B的长.
二、填空题
11．{0，2} 12．θ－π 13．
14．
15．
16．－π
三、解答题
17．解：
为实数，而
可见a也为实数，∴a，b可比较大小.
18．解：
∴Z对应的点的轨迹是以
对应的点为圆心，以
为半径的圆，但应除去原点.
19．解：设
在抛物
线
则点R的轨迹为抛物线y2=x，除去顶点（0，0）.
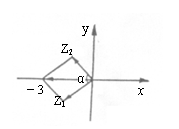20．解：
得（如图）
|
21．解：C1为椭圆：
设
把A、B两点的坐标代入直线C3的方程中，得
① 
② ①—②得
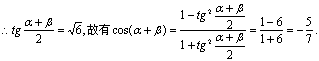
22．解：由椭圆定义，已知方程可化为
,
且
、
的方程分别为y=kx+b、
把它们分别与椭
圆方程联立，解得点Z2、Z3的坐标分别为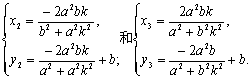
由
和两点的距离公式，化简得
①
即
②
方程②的判别式
i）当
，方程②有相异二实根，则方程①有相异三实根，此时有三个△Z1Z2Z3；
ii）当
由②得k=1，则①有一个实根，此时有1个△Z1Z2Z3；
iii）当
方程②无实根，则①有1个实根，此时有1个△Z1Z2Z3.
综上可知，当
时，有3个△Z1Z2Z3；当
时，有1个△Z1Z2Z3.