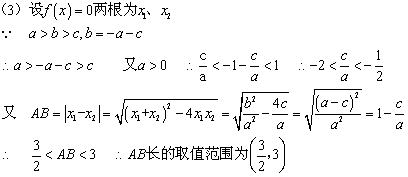高考数学复习测试试题
数学试题
本试题分第Ⅰ卷(填空题)和第Ⅱ卷(非选择题)两部分,共160分,考试时间为120分钟.
一、填空题(本大题共14小题,每小题5分,共30分,请将答案直接填写在答题卷上,不要写出解答过程)
1、若![]() ,则
,则![]() = .
= .
2、若函数![]() ,则
,则![]() __________
__________
3、设![]() 均为正数,且
均为正数,且![]() ,
,![]() ,
,![]() ,则
,则![]() 的大小关系是
的大小关系是
4、设二次函数![]() 在
在![]() 上有最大值4,则实数a的值为
上有最大值4,则实数a的值为
5、根据表格中的数据,可以判定方程ex-x-2=0的一个根所在的区间为
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
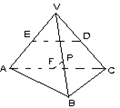 6、如右图所示,正三棱锥V-ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成的角的大小是
6、如右图所示,正三棱锥V-ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成的角的大小是
7、给出下列关于互不相同的直线![]() 和平面
和平面![]() 的四个命题:
的四个命题:
①![]() 则
则![]() 与m不共面;
与m不共面;
②![]() 、m是异面直线,
、m是异面直线,![]() ;
;
③若![]() ;
;
④若![]() ,则
,则![]()
其中真命题是 (填序号)
8、式子![]() 值是____________.
值是____________.
9、正四棱锥的底面边长为![]() ,体积为
,体积为![]() ,则它的侧棱与底面所成角的大小为 。
,则它的侧棱与底面所成角的大小为 。
10、已知长方体A1B1C1D1—ABCD中,棱AA1=5,AB=12,那么直线B1C1和平面A1BCD1的距离是______。
11、若直线ax+by=1与圆![]() 相交,则点P(a,b)与圆的位置关系是 (填在圆上或圆外或圆内)
相交,则点P(a,b)与圆的位置关系是 (填在圆上或圆外或圆内)
12、若方程![]() 无实数解,则实数
无实数解,则实数![]() 的取值范围是
的取值范围是
13、两直线3x+2y+m=0和(m2+1)x-3y-3m=0的位置关系是 (相交、平行、重合)
14、已知圆![]() ,过点A(1,0)与圆
,过点A(1,0)与圆![]() 相切的直线方程为 .
相切的直线方程为 .
二、解答题:(本大题共6小题,共90分,要求写出解答过程或证明过程)
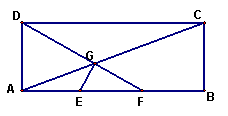 15、(本小题满分14分)如图,在矩形ABCD中,已知AB=3AD,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系,证明:
15、(本小题满分14分)如图,在矩形ABCD中,已知AB=3AD,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系,证明:![]()
 16、(本题满分14分)如图,长方体
16、(本题满分14分)如图,长方体![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)求证:直线![]() ∥平面
∥平面![]() ;(2)求证:平面
;(2)求证:平面![]()
![]() 平面
平面![]() ;
;
(3)求证:直线![]()
![]() 平面
平面![]() .
.
17、(本题满分14分)函数![]() 满足:(1)定义域是
满足:(1)定义域是![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)对任意
;(3)对任意![]() ,总有
,总有![]() 。回答下面的问题
。回答下面的问题
(1)求出![]() 的值
的值
(2)写出一个满足上述条件的具体函数
(3)判断函数![]() 的单调性,并用单调性的定义证明你的结论。
的单调性,并用单调性的定义证明你的结论。
18、(本题满分16分)已知⊙![]() :
:![]() 和定点
和定点![]() ,由⊙
,由⊙![]() 外一点
外一点![]() 向⊙
向⊙![]() 引切线
引切线![]() ,切点为
,切点为![]() ,且满足
,且满足![]() .
.
(1) 求实数![]() 间满足的等量关系;
间满足的等量关系;
(2) 求线段![]() 长的最小值;
长的最小值;
(3) 若以![]() 为圆心所作的⊙
为圆心所作的⊙![]() 与⊙
与⊙![]() 有公共点,试求半径取最小值时的⊙
有公共点,试求半径取最小值时的⊙![]() 方程.
方程.
19、(本题满分16分)如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到![]() 点,且
点,且![]() 在平面BCD上的射影O恰好在CD上.
在平面BCD上的射影O恰好在CD上.
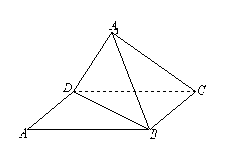 (Ⅰ)求证:
(Ⅰ)求证:![]() ;(Ⅱ)求证:平面
;(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
20、(本题满分16分)已知二次函数![]() ,
,
(1)
若![]() 且
且![]() ,证明:
,证明:![]() 的图像与x轴有两个相异交点;
的图像与x轴有两个相异交点;
(2)
若x1, x2, 且x1<x2,![]() ,证明:方程
,证明:方程![]() 必有一实根在区间 (x1, x2) 内;
必有一实根在区间 (x1, x2) 内;
(3) 在(1)的条件下,设两交点为A、B,求线段AB长的取值范围.
江苏省徐州市四星级重点高中高三联考
数学试题参考答案
一、填空题:
1、 2、1 3、![]() 4、
4、![]() 或
或![]() 5、(1,2) 6、
5、(1,2) 6、![]() 7、①②④ 8、2 9、
7、①②④ 8、2 9、![]() 10、
10、![]() 11、圆内 12、
11、圆内 12、![]() 13、相交 14、
13、相交 14、![]() 或
或![]()
二、解答题:
15、解:以A为原点,AB所在直线为x轴,建立平面直角坐标系。 ……(2分)
设AD=1,则AB=3,
从而A(0,0)、B(3,0)、C(3,1)、D(0,1)、E(1,0)、F(2,0)。……(4分)
由A(0,0)、C(3,1)知直线AC的方程为:x-3y=0,
由D(0,1)、F(2,0)直直线DF的方程为:x+2y-2=0, ……(6分)
由![]() 得
得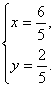 故点G的坐标为
故点G的坐标为![]() 。
……(8分)
。
……(8分)
又点E的坐标为(1,0),故![]() ,
,
所以![]() 。
……(10分)
。
……(10分)
 16、略
16、略
17、解:(1)令![]() ,有
,有![]() ,
,![]()
(2)![]() ,其中
,其中![]() 可以取
可以取![]() 内的任意一个实数
内的任意一个实数
(3)![]() 在
在![]() 单调递减
单调递减
事实上,设![]() ,且
,且![]() ,则
,则![]()
![]() ,
,![]() 在
在![]() 上单调递减
上单调递减
18、解:(1)连![]()
![]() 为切点,
为切点,![]() ,由勾股定理有
,由勾股定理有![]()
又由已知![]() ,故
,故![]() .即:
.即:![]() .
.
化简得实数a、b间满足的等量关系为:![]() . (3分)
. (3分)
(2)由![]() ,得
,得![]() .
.
![]()
![]() =
=![]() .
.
故当![]() 时,
时,![]() 即线段PQ长的最小值为
即线段PQ长的最小值为![]() (7分)
(7分)
(3)设![]() P 的半径为
P 的半径为![]() ,
,![]()
![]() P与
P与![]() O有公共点,
O有公共点,![]() O的半径为1,
O的半径为1,
![]() 即
即![]() 且
且![]() .
.
而![]() ,
,
故当![]() 时,
时,![]() 此时,
此时, ![]() ,
,![]() .
.
得半径取最小值时![]() P的方程为
P的方程为![]() .
(12分)
.
(12分)
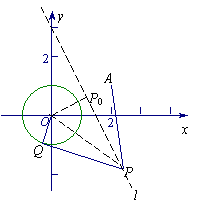 解法2:
解法2: ![]() P与
P与![]() O有公共点,
O有公共点,![]() P半径最小时为与
P半径最小时为与![]() O外切(取小者)的情形,而这些半径的最小值为圆心O到直线l的距离减去1,圆心P为过原点与l垂直的直线l’ 与l的交点P0.
O外切(取小者)的情形,而这些半径的最小值为圆心O到直线l的距离减去1,圆心P为过原点与l垂直的直线l’ 与l的交点P0.
r = -1 = -1.
又 l’:x-2y = 0,
解方程组![]() ,得
,得![]() .即P0( ,).
.即P0( ,).
∴所求圆方程为![]() . (12分)
. (12分)
19、证明:(Ⅰ)略 (Ⅱ)略 (Ⅲ)48
20、