海淀区高三年级第二学期期中练习
数 学（文科）
参考公式：
三角函数的和差化积公式
一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．圆
的圆心在直线
上，则实数m的值为 （ ）
A．1 B．－1 C．2 D．－2
2．设全集为实数集R，集合A=
，B=
，则 （ ）
A．
=R B．
=R C．
D．
3．
的值等于 （ ）
A．
B．
C．－
D．－
4．三角形ABC的三个内角A、B、C的对边分别是a、b、c.若A=60°,B=75°,a= 
，则
c的值 （ ）
A．等于2 B．等于4 C．等于
D．不确定
5．将直线
向左平移3个单位，再向上平移2个单位得到直线
，则直线
之间的距离为 （ ）
A．
B．
C．
D．
6．6名运动员站在6条跑道上准备参加比赛，其中甲不能站在第一道也不能站在第二道，乙必须站在第五道或第六道，则不同排法种数为 （ ）
A．144 B．96 C．72 D．48
7．已知直线m与平面α相交于一点P则在平面α内 （ ）
A．存在直线与直线m平行，也存在直线与直线m垂直
B．存在直线与直线m平行，但不一定存在直线与直线m垂直
C．不存在直线与直线m平行，但必存在直线与直线m垂直
D．不存在直线与直线m平行，也不一定存在直线与直线m垂直
8．已知抛物线方程为
、
.则“此抛物线顶点在直线y=x下方”
是“关于x的不等式
有实数解”的 （ ）
A．充分非必要条件 B．必要非充分条件
C．充分必要条件 D．既非充分也非必要条件
二、填空题：本大题共6小题，每小题5分，共30分，把答案填在题中横线上.
9．圆锥底面半径为1，其母线与底面所成的角为60°，则它的侧面积为 ；它的体积为 .
10．函数
的定义域为
；
若
则x的取值范围是
.
11．双曲线
的焦点坐标为
;其渐近线方程是
.
12．函数
的最小正周期为
；在区间[－π，π]上.当y取得最小值时，x的值为 .
13．不等式
的解集为
；若不等式
的解集为
，则实数a的取值范围是
.
14．等差数列
，其前6项和为24，则其首项a1为
；数列
的前9项和等于
.
三、解答题：本大题共6个小题，共80分.解答应写出文字说明，证明过程或演算步骤.
15．（本小题满分12分）
已知复平面内点A、B对应的复数分别是
，其中
对应的复数为z.
（Ⅰ）求复数z;
（Ⅱ）若复数z对应的点P在y=
上，求
的值.
16．（本小题满分14分）
已知等比数
的首项
，数列
满足首项b1=a（a为常数）.且
（1）求数列的通项公式；
（2）求数列的前n项和Sn（写成关于n的表达式）.
|
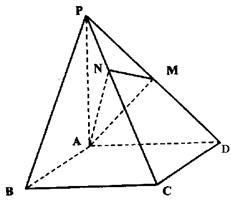
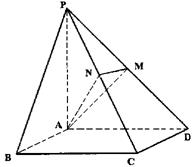
如图，四棱锥P—ABCD的底面是正方形,PA⊥底面ABCD，PA=AD=2，点M、N分别为棱PD、PC的中点.
（1）求证：PD⊥平面AMN；
（2）求三棱锥P—AMN的体积；
（3）求二面角P—AN—M的大小.
18．（本小题满分13分）
已知椭圆的中心在原点，其一条准线方程为x=－4，它的一个焦点和抛物线y2=4x的焦点重合.
（1）求该椭圆的方程；
（2）过椭圆的右焦点且斜率为k（k≠0）的直线l和椭圆分别交于点A、B，线段AB的垂直平分线和x轴相交于点P（m，0），求实数m的取值范围.
19．（本小题满分13分）
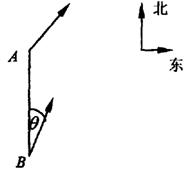
甲船由A岛出发向北偏东45°的方向作匀速直线航行，速度为15
浬/小时，在甲船
从A岛出发的同时，乙船从A岛正南40浬处的B岛出发，朝北偏东θ（其中θ为锐角，
且
的方向作匀速直线行驶，速度为10
浬/小时.如图所示.
|
（2）两船在航行中能否相遇？试说明理由.
20．（本小题满分13分）
集合A是由适合以下性质的函数f (x) 组成的,对于任意的
，
上是增函数.
（1）试判断
？若不在集合A中，
试说明理由；
（2）对于（1）中你认为是集合A中的函数
，不等式
是否对于任意的
总成立？证明你的结论.
数学（文科）参考答案及评分标准
一、选择题（每小题5分，共40分）
1.A 2.B 3.C 4.C 5.B 6.A 7.C 8.A
二、填空题（每小题5分，其中第一空3分，第二空2分；共30分）
9．2π；
10．
；（3，
11．
；
12．4π；－π
13．
；
14．9； 41
三、解答题（共80分）
15．（本小题满分12分）
解：（1）
……………………3分
………………5分
（2）点P的坐标为
………………6分
由点P在直线
上，即
.………………9分
……………………12分
16．（本小题满分14分）
解：（1）
， 
成等比数列，
且公比q=a.……………………3分
因此，数列
的通项公式为：
…………5分
（2）由（1）知，
，……7分
（常数）
即
是以a为首项，a2为公比的等比数列，……10分
|
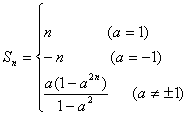…………14分
17．（本小题满分15分）
（1）证明：∵ABCD是正方形，∴CD⊥AD
∵PA⊥底面ABCD
∴AD是PD在平面ABCD内的射影，
∴CD⊥PD……………………3分
在△PCD中，M、N分别是PD、PC的中点，
则MN//CD，∴MN⊥PD
在△PAD中，PA=AD=2，M为PD的中点.
∴AM⊥PD 则PD⊥平面AMN……………………………………5分
（2）解：∵CD⊥AD，CD⊥PD ∴CD⊥平面PAD. ∵MN//CD，∴MN⊥平面PAD
又∵AM
平面PAD ∴MN⊥AM，∠AMN=90°.
在Rt△PAD中，PA=AD=2，M为PD的中点.
∴AM=PM=. 又MN=
CD=1
……………………8分
∵PM⊥平面AMN， ∴PM为三棱锥P—AMN的高.
.…………………………10分
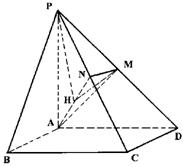
（3）解：作MH⊥AN于H，连接PH
|
∴∠PHM为二面角P—AN—M的平面角…………13分
∵PM⊥平面AMN，∴PM⊥MH.
在Rt△AMN中，
在Rt△PMH中，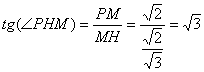
则二面角P—AN—M的大小为60°………………15分
18．（本小题满分13分）
解：（1）抛物线
的焦点坐标为（1，0）.……………………1分
设椭圆的方程为：
由题意得
…………2分
又
所求椭圆方程为：
……5分
（2）设直线
的方程为
将其代入椭圆方程，得
整理得：
……7分 显然k可以是不为0的任意实数
设
、
，AB中点
则
.
………………9分
AB的垂直平分线方程为：
令
……………………11分
|
…………13分
19．（本小题满分13分）
解：以A为原点. BA所在的直线为y轴建立如图所示的
平面直角坐标系.
设在t时刻甲、乙两船分别在点
，
的位置.
则
……2分
由
，
直线BQ的方程为
.
.
………………5分
（1）令
，P、Q两点的坐标分别为（45，45），（30，20）
.
即两船出发后3小时，相距
浬.……………………8分
（2）射线AP方程为
，射线BQ的方程为
它们的交点M（40，40）.……………………9分
若甲、乙两船相遇，则应在M点处.
此时
.甲到达M点所用时间为：
（小时）.………………10分
.乙到达M点所用时间为：
（小时）……12分 
甲、乙两船不会相遇.……13分
20．（本小题满分13分）
解：（1）函数
不在集合A中.………………3分
这是因为当
不满足条件：…………5分
在集合A中. …………………………8分
（2）
…10分
=
对于任意总成立.……………………13分