高淳县2006届高三年级十二月份模拟试题
数 学
第I卷（选择题，共60分）
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．定义
，若
,
,则
= D
A．
B．
C．
D．
2．点P(2，－1)为圆 (x－1) 2＋y2=25内弦AB中点，则直线AB的方程是A
A、x－y－3=0 B、2x＋y－3=0 C、x＋y－1=0 D、2x－y－5=0
3．命题p：若a、b∈R，则a+b>1是a+b>1的必要条件。 命题q：函数
的值域是
，则C
A．p或q为假 B．p且q为假
C．p且q为真 D．非p或非q为真
4．已知
A
A． 
B．
C． 
D． 
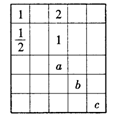5．在如图的表格中，每格填上一个数字后，使每一横行成等差数列，每一纵列成等比数列，则
的值为A
A．1 B．2 C．3 D．4
6．已知
的定义域是一切实数,则实数
的取值范围是D
A．
B．
C．
D．
7．球面上有三个点，其中任意两个点的球面距离都等于大圆周长的，经过这三个点的小圆周长为
，那么这个球的半径为 B
A．4 B．2 C．2 D．
8．将正方体AC
的6个面涂色，任何相邻两个面不同色，现在有5种不同的颜色，并且涂好了过顶点A的3个面的颜色，那么余下3 个面的涂色方案共有C
A． 15种 B．14种 C．13种 D．12种
9．已知集合
，
, (
可以等于
)，从集合
中任取一元素，则该元素的模为
的概率为D
A．
B．
C．
D．
10．设P是双曲线
上一点，双曲线的一条渐近线方程为
，
、
分别是双曲线的左、右焦点。若
，则
A
A．7
B．6
C．
或
D．9
11. 定义在R上的偶函数
，满足
，在区间［-2,0］上单调递减，设
，则
的大小顺序为A
A．
B． 
C．
D．
12．空间有四个不共面的点，它们能确定的平面数为m，而与这四点距离相等的平面有n个，则m－n=D
A．0 B．1 C．2 D．3
第Ⅱ卷（非选择题 共90分）
二、填空题（本大题共4小题，每小题4分，共16分）
13．设集合
，若点
，则
的取值范围为: 
。
14．
展开式中，不含
的项是: 
。
15．一只酒杯的轴截面是抛物线的一部分，它的函数解析式是
，在杯内放一个玻璃球，要使球触及酒杯底部，则玻璃球的半径r的取值范围是: 
。
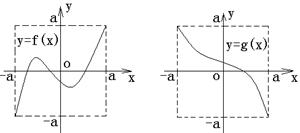16、定义域和值域均为
（常数
）的函数
和
的图像如图所示，给出下列四个命题：
（1）方程
有且仅有三个解；
（2）方程
有且仅有三个解；
（3）方程
有且仅有九个解；
（4）方程
有且仅有一个解。
那么，其中正确命题的个数是: (1)， (4)
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）
如图圆内接四边形ABCD中，
=
，
，角C为锐角，圆的半径是
，O是圆心 。
（1）求角
和
;
（2）求
.
解：（1）由正弦定理
，得
，又由题意知
是锐角，∴
…………3分
由余弦定理
得
显然
是锐角，∴
，又圆心角
∴
…………6分
（2）易见三角形BCD是正三角形 ∴
…………8分
∴
…………10分
…………12分
18．（本小题满分12分）
设一部机器在一天内发生故障的概率为0.2，机器发生故障时全天停止工作.若一周5个工作日里均无故障，可获利润10万元；发生一次故障可获利润5万元，只发生两次故障可获利润0万元，发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少？（精确到0.001）
．以X表示一周5天内机器发生故障的天数，则X－B (5，0.2)，于是X有概率分布P(X=k)=C
0.2k0.85－k,k=0,1,2,3,4,5. …………4分
以Y表示一周内所获利润，则
Y=g(X)=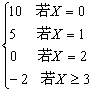
…………6分
Y的概率分布为：
P(Y=10)=P(X=0)=0.85=0.328
P(Y=5)=P(X=1)=C
0.2·0.84=0.410
P(Y=0)=P(X=2)=C
·0.22·0.83=0.205
P(Y=－2)=P(X≥3)=1－P(X=0)－P(X=1)－P(X=2)=0.057…………10分
故一周内的期望利润为：
EY=10×0.328+5×0.410+0×0.205－2×0.057=5.216(万元) …………12分
19．（本小题满分12分）
如图，四棱锥P—ABCD的底面是平行四边形，侧棱PD
底面ABCD，PD=DC=2，BD=
,BC=1, E，F分别是PC，PB的中点，点Q在直线AB上.
(1)求点A到直线EF 的距离；
(2)若QFBD，试求二面角D—EF—Q的平面角的余弦值.
解：（1）∵BD=,BC=1，CD=2
∴CB⊥BD，又PD⊥平面BCD ∴PD⊥CB …………2分
∴CB⊥平面PBD，显然EF∥BC∥AD
∴EF⊥平面PBD，∴EF⊥DF …………4分
即DF是点A到直线EF的距离，易见DF=
…………6分
（2）取BD的中点O，则OF∥PD，
故OF⊥平面BCD，∴OQ为FQ在平面BCD的射影，
∵FQ⊥BD∴ OQ ⊥BD …………8分
∴OQ∥BC∥EF，又DF⊥EF，而OF⊥EF
∴
是所求二面角的平面角 …………10分
∴所以所求二面角的余弦值是
…………12分
20．（本小题满分12分）
已知函数
在
上最小值是
，
（1）求
；
（2）若
，试比较
与
的大小.
解：1）由
，得
，…………2分
令
，得
，
显然当
时，
，
当
时，
，…………4分
因而
在
上当取得最小值
，
即
…………6分
（2)由题设：
，…………8分
易知
…………10分
而函数
在
上是减函数，
…………12分
21．（本小题满分12分）
已知函数
在
上单调递减，在
上单调递增，且方程
有3个实根：
（1）求
的取值范围；
（2）
是否有最小值？若有，求出最小值；若没有，请说明理由.
…………1分
是
单调递减，且在
上单调递增，
…………2分
=0 
…………3分
的两根为
，
又
在上单调递增，则
即
…………5分
的取值范围是
…………6分
（2）由于
是方程的三个根，所以可设
…………8分
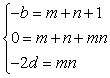…………10分
所以
有最小值112 …………12分
22．（本小题满分14分）
已知椭圆C的中心在原点，焦点在x轴上，一条经过点（3，－
）且方向向量为
的直线l交椭圆C于A、B两点，交x轴于M点，又
.
（1）求直线l方程；
（2）求椭圆C长轴长取值的范围.
解：（1）直线l过点（3，－
）且方向向量为
化简为：
…………（4分）
（2）设直线
交于两点A（x1,y1），B（x2,y2），和x轴交于M（1，0）
由
…………………（7分）
将
……①
|
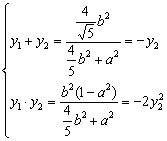
由②2/③ 知：32b2=（4b2+5a2）（a2－1）…………………………………………（10分）
化为
………………………………………………④
对方程①求判别式，且由△>0
即
化简为：
………………………………………………⑤ 12分
由④式代入⑤可知：
又椭圆的焦点在x轴上，
则
由④知：
因此所求椭圆长轴长2a范围为（