高2005级第二次月考数学试题
-------------命题人:黎光礼
(各位考生注意:本试题文理同卷,请分清自己的科别及试题)
一、选择题:本题共12题,每小题5分,满分60分。
1、设集合![]() ,
,![]() ,若M∩N=Φ,则实数
,若M∩N=Φ,则实数![]() 的取值范围是( ).
的取值范围是( ).
| A、 | B、 | C、 | D、 |
2、命题“p或q”是假命题,则下列判断正确的是( ).
| A、命题“非p”与“非q”真假不同 | B、命题“非p”与“非q”至多一个是真命题 |
| C、命题“非p”或“非q”是假命题 | D、命题“非p”且“非q”是真命题 |
3(理科)、如果不等式![]() <1成立的充分非必要条件是
<1成立的充分非必要条件是![]() ,则实数a的取值范围是( ).
,则实数a的取值范围是( ).
| A、 | B、 | C、 | D、 |
(文科)、条件“![]() ”是条件“
”是条件“![]() ”的( )条件.
”的( )条件.
| A、充分非必要 | B、必要非充分 | C、充要 | D、非充分又非必要 |
4、函数![]() 的反函数是( ).
的反函数是( ).
| A、 | B、 |
| C、 | D、 |
5、拟定从甲地到乙地通话![]() 分钟的电话费由
分钟的电话费由![]() 给出,其中
给出,其中![]() ,[m]是大于或等于
,[m]是大于或等于![]() 的最小整数(如[3]=3,[3.7]=4, [3.1]=4),则从甲地到乙地通话时间为5.5分钟的话费为( ).
的最小整数(如[3]=3,[3.7]=4, [3.1]=4),则从甲地到乙地通话时间为5.5分钟的话费为( ).
| A、3.71 | B、3.97 | C、4.24 | D、4.77 |
6、设![]() ,实数
,实数![]() 满足
满足![]() ,则y关于x的函数图像大致形状是( ).
,则y关于x的函数图像大致形状是( ).
|
A B C D
7、定义域为![]() 的函数
的函数![]() 是偶函数且在
是偶函数且在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,又
上是减函数,又![]() ,则
,则![]() ( ).
( ).
| A、在 | B、 在 |
| C、在 | D、在 |
8、已知函数![]() 是
是![]() 上的偶函数,当
上的偶函数,当![]() 时的解析式为
时的解析式为![]() ,且直线
,且直线![]() 是
是![]() 的一条对称轴,则
的一条对称轴,则![]() 在
在![]() 的解析式是( ).
的解析式是( ).
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、已知![]() 是定义在R上的奇函数,且是周期为2的周期函数,当
是定义在R上的奇函数,且是周期为2的周期函数,当![]() 时,
时,![]() ,
,
则![]() 的值为 ( ).
的值为 ( ).
| A、-5 | B、 | C、 | D、-6 |
10、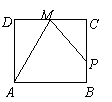 如图,点P在边长为1的正方形ABCD边上运动,设点M是CD边的中点,点P沿A®B®C®M运动时,点P经过的路程记为x,△APM的面积为y,则函数y=f(x)的图象只可能是( ).
如图,点P在边长为1的正方形ABCD边上运动,设点M是CD边的中点,点P沿A®B®C®M运动时,点P经过的路程记为x,△APM的面积为y,则函数y=f(x)的图象只可能是( ).
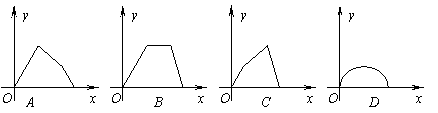
11、已知定义在实数R上的函数![]() 不恒为零,同时满足
不恒为零,同时满足![]() 且当x>0时,
且当x>0时,![]() ,那么当
,那么当![]() 时,一定有( ).
时,一定有( ).
| A、 | B、 | C、 | D、 |
12(理科)、方程![]() 有五个不相等的实数根,则这五根之和为( ).
有五个不相等的实数根,则这五根之和为( ).
| A、5 | B、10 | C、 | D、 |
(文科)、方程![]() 有负根,则实数a的取值范围为( ).
有负根,则实数a的取值范围为( ).
| A、 | B、 | C、 | D、 |
二、填空题:本题共4小题,每小题4分,满分16分.
13、函数![]() 在区间[2,4]上的最大值是_______.
在区间[2,4]上的最大值是_______.
14(理科)、函数![]() 上是增函数,则数p的取值范围是_______.
上是增函数,则数p的取值范围是_______.
(文科)、若![]() 则 0、1、
则 0、1、![]() 、
、![]() 的大小关系是_______.
的大小关系是_______.
15(理科)、设奇函数![]() 上是增函数,且
上是增函数,且![]() 若函数
若函数![]() 对所有的
对所有的![]() 都成立,当
都成立,当![]() 时,则t的取值范围是_______.
时,则t的取值范围是_______.
(文科)、若奇函数![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,则不等式
,则不等式![]() 的解为_______.
的解为_______.
16、已知函数![]() 的图象与函数g(x)的图象关于直线
的图象与函数g(x)的图象关于直线![]() 对称,令
对称,令![]() 则关于函数
则关于函数![]() 有下列命题:
有下列命题:
①![]() 的图象关于原点对称; ②
的图象关于原点对称; ②![]() 为偶函数;
为偶函数;
③![]() 的最小值为0; ④
的最小值为0; ④![]() 在(0,1)上为增函数.
在(0,1)上为增函数.
其中正确命题的序号为 (注:将所有正确命题的序号都填上).
高2005级第二次月考数学试题
答 题 卷
一、选择题:本题共12题,每小题5分,满分60分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:本题共4小题,每小题4分,满分16分.
13、 . 14、 .
15、 . 16、 .
三、解答题:本题共6小题,满分74分.
17、(文科12分)已知![]() (1≤x≤4),
(1≤x≤4),
求:函数![]() 的最大值和最小值.
的最大值和最小值.
18、(12分)设函数![]()
![]()
![]() 为奇函数,又
为奇函数,又![]() ,且
,且![]() 在
在![]() 上递增.
上递增.
⑴求![]() 的值;
的值;
⑵当![]() 时,讨论
时,讨论![]() 的单调性.
的单调性.
19、(12分)已知![]()
![]()
![]() 成立的自变量x的取值范围.
成立的自变量x的取值范围.
20、(12分)已知某商品的价格上涨![]() %,销售的数量就减少
%,销售的数量就减少![]() %,其中
%,其中![]() 为正的常数.
为正的常数.
(1)当![]() 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?
(2)如果适当地涨价,能使销售总金额增加,求![]() 的取值范围.
的取值范围.
21、 ( 12分)已知![]() ,点
,点![]() 是函数
是函数![]() 图象上任意一点,点
图象上任意一点,点![]() 关于原点的对称点Q的轨迹是函数
关于原点的对称点Q的轨迹是函数![]() 的图象,当
的图象,当![]() 时,有
时,有![]() 恒成立.
恒成立.
(1)求出![]() 的表达式;
的表达式;
(2)求![]() 的取值范围.
的取值范围.
22、(理科12分,文科14分)设![]() 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称。且当
对称。且当![]() 时,
时,![]()
求函数![]() 的表达式;
的表达式;
在![]() 或
或![]() 的情况下,分别讨论函数
的情况下,分别讨论函数![]() 的最大值,并指出
的最大值,并指出![]() 为何值时,
为何值时,![]() 的图像的最高点恰好落在直线
的图像的最高点恰好落在直线![]() 上
上
23、(理科14分) 已知二次函数![]() 均为实数),满足
均为实数),满足![]() ,对于任意实数
,对于任意实数![]() 都有
都有![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)证明:![]() ;
;
(Ⅲ)当![]() 且
且![]() 取得最小值时,函数
取得最小值时,函数![]()
![]() 是单调的,求证:
是单调的,求证:![]() .
.
答 题 卷
一、选择题:本题共12题,每小题5分,满分60分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | D | B/A | D | C | A | B | A | C | A | D | C/C |
二、填空题:本题共4小题,每小题4分,满分16分。
13、
![]() 14、理
14、理![]() ;文
;文![]()
15、理![]() ;文
;文![]() 16、②,③,④
16、②,③,④
三、解答题:本题共6小题,满分74分.
17、(文科作理科不作。12分)已知![]() (1≤x≤4),求:函数
(1≤x≤4),求:函数![]() 的最大值和最小值。
的最大值和最小值。
解:∵f (x)的定义域为[1, 4]
∴g(x)的定义域为[1, 2]
∵![]()
∵1≤x≤2
∴![]()
∴当x = 1时, g (x)max = 2 ;当x = 2时, g (x)min = 7
18、(12分)设函数![]()
![]()
![]()
![]() 为奇函数,又
为奇函数,又![]() ,且
,且![]() 在
在![]() 上递增。 ⑴求
上递增。 ⑴求![]() 、
、![]() 、
、![]() 的值; ⑵当
的值; ⑵当![]() 时,讨论
时,讨论![]() 的单调性.
的单调性.
解:⑴∵![]() 为奇函数,∴
为奇函数,∴![]() ,……2分
,……2分
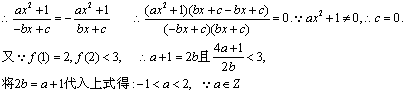
∴![]() =0或
=0或![]() =1。而
=1。而![]() =0时
=0时![]() =
=![]() ,
,![]() 矛盾。………5分
矛盾。………5分
∴![]() =1,
=1,![]() =1,
=1,![]() =0;………7分
=0;………7分
⑵由⑴![]()
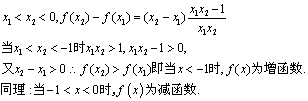
19、(12分)已知![]()
![]()
![]() 成立的自变量x的取值范围.
成立的自变量x的取值范围.
解:依题意有![]()
当a>1时,原不等式等价于
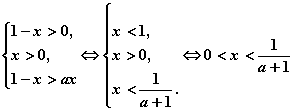
当![]() 时,原不等式等价于
时,原不等式等价于
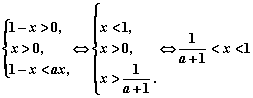
综上所述:
(1)当![]() 时,使
时,使![]() 成立的自变量x的取值范围是
成立的自变量x的取值范围是![]()
(2)当![]() 时,当
时,当![]() 成立的自变量x的取值范围是
成立的自变量x的取值范围是![]()
20、(12分)已知某商品的价格上涨![]() %,销售的数量就减少
%,销售的数量就减少![]() %,其中
%,其中![]() 为正的常数。
为正的常数。
(1)当![]() 时,该商品的价格上涨多少,就%%能使销售的总金额最大?
时,该商品的价格上涨多少,就%%能使销售的总金额最大?
(2)如果适当地涨价,能使销售总金额增加,求![]() 的取值范围
的取值范围
解:(1)设商品现在定价![]() 元,卖出的数量为
元,卖出的数量为![]() 个。
个。
由题设:当价格上涨x%时,销售总额为![]() ,
,
即 ![]() ,(
,(![]() ),
),
取![]() 得:
得:![]() ,当
,当![]() 时,
时,![]() ,
,
即:该商品的价格上涨50%时,销售总金额最大。
(2)二次函数![]() ,
,
在 ![]() 上递增,在
上递增,在![]() 上递减,
上递减,
适当地涨价能使销售总金额增加,即 在![]() 内存在一个区间,使函数
内存在一个区间,使函数![]() 在此区间上是增函数,所以
在此区间上是增函数,所以 ![]() ,
解得
,
解得![]() ,即所求
,即所求![]() 的取值范围是
的取值范围是![]() .
.
21.( 12分)已知f(x)=loga(x+1),点P是函数y=f(x)图象上的任意一点,点P关于原点的对称点Q的轨迹是函数y=g(x)的图象,当a>1,x∈[0,1![]() 时,总有2f(x)+g(x)≥m恒成立.
时,总有2f(x)+g(x)≥m恒成立.
(1)求出g(x)的表达式;
(2)求m的取值范围.
解:(1)设Q(x,y)![]() P(-x,-y),代入f(x)方程得, g(x)=-loga(-x+1). 4分
P(-x,-y),代入f(x)方程得, g(x)=-loga(-x+1). 4分
(2)2f(x)+g(x)≥m恒成立![]() 2loga(x+1)-loga(1-x)≥m恒成立
2loga(x+1)-loga(1-x)≥m恒成立![]() loga
loga![]() ≥m恒成立,即m小于等于loga
≥m恒成立,即m小于等于loga![]() 的最小值.
的最小值.
令h(x)=![]()
=![]() . 8分
. 8分
易证h(x)在x∈[0,1)上单调递增,
∴h(x)min=h(0)=1,
又∵a>1,∴loga![]() ≥loga1=0, 即loga
≥loga1=0, 即loga![]() 的最小值为0,
的最小值为0,
∴m的取值范围是m≤0.
22、(12分)设f(x)是定义在[-1,1]上的偶函数,g(x)与f(x)的图象关于直线![]() 对称。且当
对称。且当![]() 时,
时,![]()
求函数f(x)的表达式;
在![]() 或
或![]() 的情况下,分别讨论函数f(x)的最大值,并指出
的情况下,分别讨论函数f(x)的最大值,并指出![]() 为何值时,f(x)的图像的最高点恰好落在直线
为何值时,f(x)的图像的最高点恰好落在直线![]() 上
上
讲解 (1)注意到![]() 是定义在区间
是定义在区间![]() 上的函数,因此,根据对称性,我们只能求出
上的函数,因此,根据对称性,我们只能求出![]() 在区间
在区间![]() 上的解析式,
上的解析式,![]() 在区间
在区间![]() 上的解析式,则可以根据函数的奇偶性去求。
上的解析式,则可以根据函数的奇偶性去求。
当![]() 时,
时,![]() ,由于
,由于![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,所以,
对称,所以,![]()
当![]() 时,
时,![]() ,由
,由![]() 为偶函数,可知:
为偶函数,可知:
![]()
所以,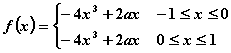
因为![]() 为偶函数,所以,
为偶函数,所以,![]() (
(![]() )的最大值,
)的最大值,
必等于![]() 在区间
在区间![]() 上的最大值。故只需考虑
上的最大值。故只需考虑![]() 的情形,
的情形,
此时,![]() 。
。
对于这个三次函数,要求其最大值,比较容易想到的方法是:考虑其单调性。
因此,我们不妨在区间![]() 上任取
上任取![]() ,设
,设![]() ,则
,则
![]()
![]()
![]()
如果![]() ,则
,则![]() ,
,
故![]() <0,即
<0,即![]() 在区间
在区间![]() 上单调递增。
上单调递增。
所以,![]() 的最大值在
的最大值在![]() 取得,为
取得,为![]() 。
。
令![]() =12可解得:
=12可解得:![]()
如果![]() ,则
,则![]() 的符号不能确定,
的符号不能确定,
为确定![]() 的单调区间,可令
的单调区间,可令![]() <0
<0
由于![]() ,要使上式成立,只需:
,要使上式成立,只需:![]() ,即
,即![]() ,
,
由此我们不难得知:![]() 在区间
在区间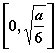 上单调递增,在区间
上单调递增,在区间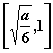 上单调递减。(证明略)
上单调递减。(证明略)
所以,![]() 在区间
在区间![]() 上的最大值为
上的最大值为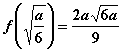 。
。
令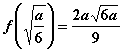 =12,解之得:
=12,解之得:![]() ,与
,与 ![]() 矛盾。
矛盾。
综上可知:当![]() 时,
时,![]() 的最大值为
的最大值为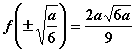 ,
,
当![]() 时,
时,![]() 的最大值为
的最大值为![]() 。
。
并且,当![]() 时,函数
时,函数![]() 的图像的最高点恰好落在直线
的图像的最高点恰好落在直线![]() 上。
上。
23、(理科14分) 已知二次函数![]() 均为实数),满足
均为实数),满足![]() ,对于任意实数x都有
,对于任意实数x都有![]()
(Ⅰ)求f(1)的值;
(Ⅱ)证明:![]() ;
;
(Ⅲ)当x∈[-2,2]且a+c取得最小值时,函数F(x)=f(x)-mx(m为实数)是单调的,求证:![]() .
.
解:(Ⅰ)∵对于任意x∈R,都有f(x)—x≥0,且当x∈(0,2)时,
有f(x)≤(![]() )2·令x=1 ∴1≤f(1)≤(
)2·令x=1 ∴1≤f(1)≤(![]() )2.即f(1)=1.……4分
)2.即f(1)=1.……4分
(Ⅱ)由a—b+c=0及f(1)=1.
有![]() 可得b=a+c=
可得b=a+c=![]() .……6分
.……6分
又对任意x,f(x)—x≥ 0,即ax2—![]() x+c≥0. ∴a>0且△≤0.
x+c≥0. ∴a>0且△≤0.
即![]() —4ac≤0。解得ac≥
—4ac≤0。解得ac≥![]() .……9分
.……9分
(Ⅲ)由(Ⅱ)可知a>0,c>0. a+c≥2![]() ≥2·
≥2·![]() =
=![]() .……10分
.……10分
![]() a=c,
a=c,
当且仅当 a+c=![]() 时等号成立。此时a=c=
时等号成立。此时a=c=![]() ……11分
……11分
∴f(x)=![]() x2+
x2+![]() x+
x+![]() , F(x)=f(x)-mx=
, F(x)=f(x)-mx=![]() [x2+(2-4m)x+1]。……12分
[x2+(2-4m)x+1]。……12分
当x∈[-2,2]时,F(x)时单调的,所以F(x)的顶点一定在[-2,2]的外边.
∴![]() ≥2。……14分 解得m≤-
≥2。……14分 解得m≤-![]() 或m≥
或m≥![]() 。……14分
。……14分
