|
数 学 试 卷
2006.5
一、选择题（本大题共12小题，每小题5分，满分共计60分）
1．满足条件
的所有集合A的个数是 （ ）
A．6 B．7 C．8 D．16
2．（理科）已知复数z和（
都是纯虚数，则z= （ ）
A．i B．－2i C．－i D．2i
（文科）函数
的初相为 （ ）
A．－
B．－
C． D．
3．命题甲：p是q 的充分条件；命题乙：p是q的充分必要条件。则命题甲是命题乙的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
4．已知α、β、γ表示平面，
、K表示直线，并且有
。给出三个结论：①
；②
；③
。其中正确的结论的个数是 （ ）
A．0 B．1 C．2 D．3
5．在平面直角坐标平面上，不等式组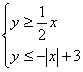
所表示的平面区域的面积等于 （ ）
A．6 B．9 C．12 D．15
6．已知m＞0，n＞0，且满足m+n=4，则下列不等式恒成立的是YCY （ ）
A．
B．
C．
D．
7．在
的展开式中，不含x的项等于 （ ）
A．－4 B．－8 C．－12 D．－20
8．现有6个人分乘两辆不同的出租车，已知每辆车最多能乘4个人，则不同的乘车方案种数为 （ ）
A．30 B．50 C．60 D．80
9．若a，b，c是三个两两互不相同的实数，其中a是b和c的等比中项，b是a和c的等差中项，则
（ ）
A．－4 B．－1 C．1 D．4
10．已知D为三角形ABC的边BC的中点，点P满足
则实数
的值为 （ ）
A．
B．2 C．－2 D．
11．过抛物线
的焦点F作直线与此抛物线相交于A、B两点。O是坐标原点，当
时，直线AB的斜率的取值范围是 （ ）
A．
B．
C．
D．
12．半径为R的球的内接正三棱正三棱柱的侧面积（各侧面面积之和）的最大值为（ ）
A．3
B． C．2
D．
二、填空题（本大题共4小题，每小题4分，满分共计16分）
13．若
，则
的终边落在第
象限；
14．已知双曲线的两条渐近线的方程是
和
，一条准线的方程是
，则此双曲线的方程是
；
15．已知可导函数f（x）的导函数为
，且满足
，则
；
16．设f（x）在其定义域R上是单调递增的奇函数，
在其定义域R上是偶函数，并且在区间
上f（x）和的图像关于x轴对称，英才苑现在给出下列条件：
①
②
③
④
其中能够使得不等式
恒成立的条件的序号是
（请把你认为正确的都填上）
三、解答题（本大题共6小题，满分共计74分）
17．（本小题满分12分）若A，B，C是三角形ABC的三个内角，向量
且
与
的夹角为。
（1）求角B的大小；
（2）求
的取值范围。
|
（1）求证：BC∥平面A1MD1；
（2）求二面角A1－D1M－C的大小。
19．（本小题满分12分）甲、乙、丙三个口袋内都分别装有6个不相同的球，并且每个口袋内的6个球均有1个红球，2个黑球，3个无色透明的球，现从甲、乙、内三个口袋中依次随机各摸出1个球。
理科：（1）求恰好摸出红球、黑球和无色球各1个的概率；
（2）求摸出的3个球中含有有色球数
的概率分布列和数学期望。
文科：（1）求恰好摸出2个黑球的概率；
（2）求恰好摸出红球、黑球和无色透明球各1个的概率；
（3）求摸出的3个球中至少有1个是有色球的概率。
20．（本小题满分12分）已知数列
的各项均为正数，它的前n项和Sn满足
，并且
成等比数列。
（1）求数列的通项公式；
（2）理科：设
，Tn是数列
的前n项和，求证：
。
文科：设
，Tn是数列的前n项和，求证：
。
21．（本小题满分12分）
理科：已知
是定义在R上的单调递增函数，
是它的反函数，并且曲线y=
在其与坐标轴交点处的切线y=在其与坐标轴交点处的切线互相平行。
（1）求和的解析式；
（2）设函数
，当x＞0且
时，不等式
恒成立，求实数m的取值集合。
文料：设函数
（1）当
时，函数的图像经过点O（0，0）和M（1，1）两点，并且在原点处取极小值，求函数的极大值；
（2）求证：当函数有极小值时，它也一定有极大值。
22．（本小题满分14分）F1、F2分别是椭圆
的左、右焦点，B是其上顶点，N是其右准线与x轴的交点，并且满足
。
（1）求此椭圆的方程；
（2）若M是坐标平面内一动点，G是三角形MF1F2的重心，且
，其中O是坐标原点，求动点M的轨迹C的方程；
（3）点P是此椭圆上一点，但非短轴端点，并且过P可作（2）中所求得轨迹C的两条不同的切线，Q、R是两个切点。
理科：求
的最小值。
文科：当＜0时，求点P 的横坐标的取值范围。
数学参考答案
一、选择题
CDBBC DDBAC DA
二、填空题
13．四 14．
15．6 16．①
三、解答题
17．解：（1）
，且与的夹角为，
即
或1。
而B是三角形的内角，
；……………………6分
（2）由（1）可知
，所以
。
。
，即
的取值范围是
。……12分
18．解：（1）
∥B1C1，B1C1∥A1D1，∴BC∥A1D1。
又A1D1
平面A1MD1，BC
平面A1MD1
∥平面A1MD1；………………………………………………5分
（2）设平面A1MD1与棱DC相交于点N，连结D1N，则点N是DC的中点。
∵A1D1⊥平面D1DCC1，A1D1平面A1MND1
∴平面A1MND1⊥平面D1DCC1，且D1N是交线。
过点C作CH⊥D1N于H点，则CH⊥平面A1MND1，
再过H作HO⊥D1M于O点，连结CO，根据三垂线定理得CO⊥D1M，
从而∠COH是二面角C－D1M－N，也就是所求二面角A1－D1M－C的补二面角的平面角。…………………………………………………………………8分
设正方体的棱长为2，则在Rt△DND1中，由于DD1=2，DN=
，所以有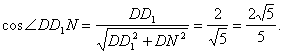
在Rt△CHN中，由于
所以有
。
又由于可求得
所以在△MD1C中有
进而有
根据三角形面积公式得
从而在Rt△CHO中，
因此所求的二面角A1－D1M－C的大小为
…………12分
向量作法：分别以直线DA、DC、DD1为x、y、z轴建立空间直角坐标系
D－xyz，并设正方体的棱长为2，则相关点的坐标分别为
A1（2，0，2），D1（0，0，2），C（0，2，0），M（2，1，0）………6分
设
是平面A1MD1的法向量，则
而且
所以有
，即
令z=1，则y=2，x=0，从而
…………………………8分
再设
是平面CMD1的法向量，则
而且
，所以有
，即
令
，则
，从而
……………………10分
设是所求二面角
的平面角，则是钝角，并且有
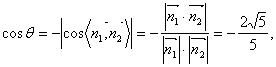
即
为所求。………………12分
19．解：由于各个袋中球的情况一样，而且从每一个袋中摸出红球、黑球、无色球的概率均分别为
，所以根据相互独立事件同时发生的概率公式可得
理科：（1）
………………………………………4分
（2）的取值为0，1，2，3，并且
；
从而的概率分布列为
|
| 0 | 1 | 2 | 3 |
| p |
| |
|
|
并且
…………………………12分
文科：（1）
；………………………………………4分
（2）
………………8分
（3）
………………12分
20．解：（1）∵对任意
，有 ①
∴当n=1时，有
，解得a1=1或2 …………2分
当n≥2时，有
②
当①－②并整理得
而{an}的各项均为正数，所以
………………6分
当a1=1时，
成立；
当a2=2时，
不成立；舍去。
所以
………………9分
（2）证明：理科：根据（1）的结论可得
所以有
即
………………12分
文科：根据（1）结论可得
所以有
即 
………………………………………………………………………12分
21．理科：解：（1）由已知条件可知：函数
，所以曲线y = f (x)只与y轴有交点M（0，a）；函数
，所以曲线y = f－1(x)只与x轴有交点N（a,0）.……………………………………………………………………………2分
对f (x)和f－1(x)求导得 
， 
，
根据条件应当有 
，即
…………………4分
而函数f (x)是定义在R上的单调增函数，所以a>0，即a = 1.
因此 
.……………………………6分
（2）由（1）可得
，从而有
当x >0且x≠1时，
恒成立.…………………7分
分以下两种情况来考虑；
①当
令
再令
当
所以有
这样此时只需m≥1即可；…………………………………9分
②当
令
再令
当
所以有
，这样此时只需m≤1即可；………………………………11分
根据题意；①②两种情形应同时成立，因此m=1，即其取值集合为{1}………12分
文科：解：（1）由于 a= －1，函数f (x)的图像经过点O（0，0）和M（1，1），所以有
.
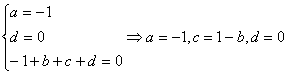从而f (x) = －x3+bx2 +(1－b)x，………………………………………………………2分
f′（x）=－3x2 + 2bx + (1－b).……………………………………………………3分
又因为函数f (x)在原点处取得极小值，所以x = 0是方程f′(x)=0的根.
所以1－b=0，b=1，进而有f (x)=－x3+x2.…………………………………………… 5分
（2）对函数f (x)求导得 f′(x) = 3ax2+2bx +c
由于f (x)有极小值，所以方程f′(x) =0有实根，又a≠0，所以方程f′(x) =0是一个一元二次方程，故可令其根为x1和x2，并且x1≤x2.……………………………………7分
假设x1=x2，则方程f′(x) =0有两相等的实根，于是f′(x) =3a (x－x1)2.从而当a>0时，f′(x)≥0恒成立；当a <0时，f′(x) ≤0恒成立，而且只有当x = x1时，才有f′(x) =0.因此函数f(x)在整个定义域R上是单调的，f (x)不可能有极小值，与已知矛盾.从而x1≠x2，x1< x2.…………………………………………………………………………………10分
当a > 0时，列表如下：
| x |
| x1 | （x1,x2） | x2 |
|
| f′(x) | + | 0 | － | 0 | + |
| f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
当a<o时，列表如下：
| x | (－∞,x1) | x1 | (x1.,x2) | x2 | (x2,+ ∞) |
| F’(x) | － | 0 | + | 0 | － |
| F(x) | ↓ | 极小值 | ↑ | 极大值 | ↓ |
由此可见，函数f（x）也一定有极大值。
22．解（1）设F1（ -c,o）F2(c,0)(c>0),则
因为
所以（2c，0）=
从而N（2c，0），B（0，c）
所以
因此所求椭圆的方程为
………………5分
（注意：此问也可以直接利用a，b，c表示出来B，F1，F2，N四个点的坐标，再代入题设所给的向量关系式中，进而求出a，b得方程）。
（2）设M（x，y），则由（1）得F1（－2，0），F2（2，0），
所以G
，从而
。
因为 所以有
由于G是三角形MF1F2的重心，即M，F1，F2应当是一个三角形的三个顶点，
因此所求的轨迹C的方程为
（y≠0）； …………9分
（3）理科：由（2）知轨迹C的方程为
即
（y≠0）。
显然轨迹C是以点C（3，0）为圆心，半径r=3的圆除去两点（0，0）和（6，0）剩余部分的部分曲线。
设P（m，n），则根据平面几何知识得
从而根据平面向量数量积的定义及均值不等式得
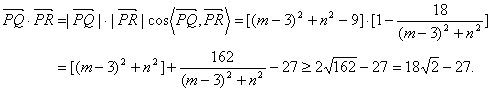
当且仅当
时，取“=” （※） …………12分
由点P（m，n）在椭圆上（非短轴端点），并且在圆外，可知
由于
，所以条件（※）的要求满足。
因此的最小值为
………………14分
文科：由（2）知轨迹C的方程为
显然轨迹C是以点C（3，0）为圆心，半径r=3的圆除去两点（0，0）和（6，0）剩余部分的部分曲线。
设P（m，n），（m≠0）则根据平面几何知识得
由于<0，所以向量
的夹角即∠QPR是一个钝角。
由圆的切线性质，得∠QPR=2∠QPC，所以∠QPC>45°
从而在Rt△QPC中，
……12分
又由条件知点P（m，n）在椭圆上，并且在圆外
所以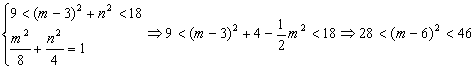
又根据条件
因此点P的横坐标的取值范围是
…………14分