|
高三名校试题汇编(75)
数 学 试 卷
2006.5
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分,考试时间120分钟。
YCY
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知集合![]() ( )
( )
A.(0,1),(1,2) B.{(0,1),(1,2)}
C.{yy=1或y=2} D.{yy≥1}
2.已知-9,![]() -1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数
-1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数
列,则b2(a2-a1)的值等于 ( )
A.-8 B.8 C.-![]() D.
D.![]()
3.设集合I是全集,![]() ,则
,则![]() 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.若a、b是异面直线,且a//平面α,那么b与平面α的位置关系是 ( )
A.b//α B.b与α相交
C.![]() D.以上三种情况都有可能
D.以上三种情况都有可能
5.函数![]() 的图象 ( )
的图象 ( )
A.与![]() 的图象关于y轴对称 B.与
的图象关于y轴对称 B.与![]() 的图象关于坐标原点对称
的图象关于坐标原点对称
C.与![]() 的图象关于y轴对称 D.与
的图象关于y轴对称 D.与![]() 的图象关于坐标原点对称
的图象关于坐标原点对称
6.正四棱锥的侧棱长与底面边长都是1,英才苑则侧棱与底面所成的角为 ( )
A.75° B.60° C.45° D.30°
7.函数![]() 的最小正周期为 ( )
的最小正周期为 ( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2![]()
8.在△ABC中,0<tanA tanB<1,则△ABC是 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.形状不确定
9.求![]() 展开式中的常项数是 ( )
展开式中的常项数是 ( )
A.-20 B.20 C.-15 D.15
10.已知向量![]() 则向量
则向量![]() 的模的取值范围是( )
的模的取值范围是( )
A.[1,3] B.[1,3![]() ] C.[
] C.[![]() ,3] D.[
,3] D.[![]() ,3
,3![]() ]
]
11.已知![]() 是R上的增函数,如果点A(-1,1)、B(1,3)在它的图象上,
是R上的增函数,如果点A(-1,1)、B(1,3)在它的图象上,![]() 是它的反函数,那么不等式
是它的反函数,那么不等式![]() 的解集为 ( )
的解集为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.已知直线![]() 不全为0)与圆
不全为0)与圆![]() 有共公点的横、纵坐标均为整数,英才苑那么这样的直线共有 ( )
有共公点的横、纵坐标均为整数,英才苑那么这样的直线共有 ( )
A.66条 B.72条 C.74条 D.78条
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上。)
|
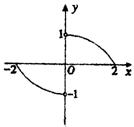
14.如图,函数![]() 的图象是中心在原点,焦点在
的图象是中心在原点,焦点在
x轴上的椭圆的两段弧,则不等式![]()
的解集为 。
15.已知直线![]() 交于A、B两点,若
交于A、B两点,若![]() ,则实数a的值是
。
,则实数a的值是
。
16.已知x,y满足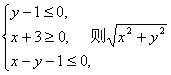 的最大值为
。
的最大值为
。
三、解答题(解答应写出文字说明,证明过程或演算步骤。共6个小题,共74分)
17.(12分)
解不等式:![]()
18.(12分)
已知函数![]()
![]() ,若
,若![]() 相邻两对称轴间的距离不小于1,求ω的最大值。
相邻两对称轴间的距离不小于1,求ω的最大值。
19.(12分)
袋中有4个红球,3个黑球,今从袋中随机取出4个球,设取到一个红球得2分,取到一个黑球得1分。
(1)(文)求可能得分ξ的取值及相应的概率;
(2)(理)求得分ξ的概率分布和数学期望。
20.(12分)
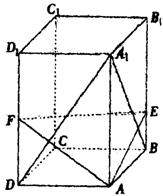
如图,正四棱柱ABCD—A1B1C1D1的底面边长是![]() ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
|
(2)求二面角A—EF—B的大小?
(3)求点B1到平面AEF的距离?
21.(12分)设![]() 的整数部分。
的整数部分。
(1)求F(1)、F(2)、F(3);
(2)求满足F(m)=3的m的值;
(3)(文)求![]()
(理)求证:F(1)+F(2)+F(3)+…+F(![]() )=(n-2)·2n+n+2 (n∈N)
)=(n-2)·2n+n+2 (n∈N)
22.(14分)
椭圆G:![]() 的两个焦点F1(-c,0),F2(c,0),M是椭圆上一点,且满足
的两个焦点F1(-c,0),F2(c,0),M是椭圆上一点,且满足![]()
(1)求椭圆的离心率e的取值范围;
(2)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为![]() 。
。
①求此时椭圆G的方程;
②(理)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B,Q为AB中点,问A、B两点能否关于过点P(![]() )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由。
)、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由。
参考答案
一、选择题(12小题,每小题5分,共60分)
1.D 2.A 3.B 4.D 5.D 6.C 7.B 8.C 9.A 10.D 11.B 12.
二、填空题(每题4分,共16分)
13.16 14.![]() 15.
15.![]() 16.5
16.5
三、解答题(共6题,共74分)
17.(12分)![]() (2分)
(2分) 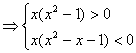 (6分)
(6分)
∴![]() (12分)
(12分)
18.(12分)![]() …………6分
…………6分
![]() …………12分
…………12分
19.(12分)(文)(1)ξ=5,6,7,8 ……………6分
相应P:![]() …………12分
…………12分
(理)(2)同上:Eξ=![]() ………………12分
………………12分
20.(12分)(1)三垂线定理证:A1C⊥AE,同理证:A1C⊥AF …………4分
∴A1C⊥平面EFA。
(2)应用相似△,可推出:二面角的大小![]() …………8分
…………8分
(3)利用等体积法求得:![]()
21.(12分)(1)F(1)=0, F(2)=1, F(3)=1 ………………3分
(2)m=8,9,10,11,12,13,14,15共8个 …………6分
(3)(文)n·2n+1 (理)用数学归纳法证明(略) …………12分
22.(14分)(1)![]() ………………7分
………………7分
(2)①在![]() 时,当y=-3时,HN2max
时,当y=-3时,HN2max
所求椭圆方程为![]() …………10分(理), 14分(文)
…………10分(理), 14分(文)
②(理)解联立方程,用判别式,利用对称可求得 ![]()
又k≠0, ∴![]() 时,
时,
A、B两点关于过点P、Q的直线对称。 …………14分