高考高三年级形成性测试模拟数学

2005—2006学年度高三年级形成性测试模拟

数 学 试 卷

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2005．12

一、选择题：（本大题共10小题，每小题5分，共50分）

1．要从已编号（1-50）的50枚最新研制的某型号导弹中随机抽取5枚来进行发射试验，用每部分选取的号码间隔一样的系统抽样方法,确定所选取的5枚导弹的编号可能是(　 )

A、5、10、15、20、25　　　　　　　  　　 B、3、13、23、33、43

C、1、2、3、4、5　　　　　　　　　　　　 D、2、4、8、16、22

2．一个样本的方差是，则这个样本的平均数与样本容量分别是（　）

A．10，10　　　　　　　　　　　  B．6，15

C．15．10　　　　　　　　　　　  D．由确定，10

3． 组成的集合中，元素最多有（　）个

A．2　　　 B.3　　　　　  C.4　　　　  D.5

4．已知集合则等于（　　）

A ．　　B． 　　C ．　　D．

5．a、b为实数，集合，，表示把集合M中的元素映射到集合N中仍为，则a+b =　　　　　 （　　）

　　　 A．　　　　　　 B．　0　　　　  　 C．　1，或2　　　　  　　　D．　

6．已知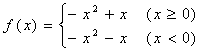，则不等式解集是（　 ）

A．　　　　　　 B．

C．　　　　　　 D．

7．若函数的图象关于原点中心对称，则

A．在[-3，3]上为增函数　　　B．在上为增函数，在上为减函数

C．在上为减函数　　　　D．在上为增函数

8．已知实系数的一元二次方程ax²＋bx＋c＝0（a≠0），（在）下列结论中正确的为（　　）

A.Δ＝b²-4ac≥0是这个方程有实根的充分条件

B.Δ＝b²-4ac≥0是这个方程有实根的必要条件

C.Δ＝b²-4ac≥0是这个方程有实根的充要条件

D.Δ＝b²-4ac＝0是这个方程有实根的充分条件

9．等于（　 ）

A．1　　　　B．0　　  C．　　　　　　 D．不存在

10．若方程有正数解，则实数的取值范围是（　　）

A．　　　　B．　　 C．　　　 D．

二、填空题：（本题每小题4分，共24分）

11．若原命题为：若p则q；则其逆命是为_________;否命题为_________；逆否命题为_________。若原命题是真命题，则_________一定为真命题.

12．“a＜b”是“ac²＜bc²”的_________条件.（a、b、c都为实数）

13．无穷数列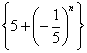 的极限是___________

14． 垂直于直线 2x －6y +1 = 0且与曲线相切的直线方程的一般形式为_______________________

15．函数在定义域内存在反函数，且

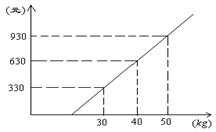
16．某航空公司规定，乘机所携带行李的重量（kg）与其运费（元）由如图的一次函数图像确定，那么乘客免费可携带行李的最大重量为 ___________。

三、解答题（本题17—20小题每题12分，21、22小题每题14分，共76分）

17．已知A＝求实数a、b的值。

18．记函数f(x)=的定义域为A, g(x)=lg[(x－a－1)(2a－x)](a<1)的定义域为B.　　　　　　 

　(1) 求A；　　 　　　　　

 (2) 若BA, 求实数a的取值范围.

19．设，定义在区间内的函数是奇函数。

（1）求的取值范围；　　　

（2）讨论函数的单调性。

20．已知命题：方程在上有解；命题：只有一个实数满足不等式若命题是假命题，求实数的取值范围。

21、已知函数的定义域为R，值域为[0,2],求m、n的值。

22、某化妆品生产企业为了占有更多的市场份额，拟在2002年度进行一系列促销活动，经过市场调查和测算，化妆品的年销量x万件与年促销ｔ万元之间满足3－x与ｔ＋1成反比例，如果不搞促销活动，化妆品的年销量只能是1万件，已知2002年生产化妆品的设备折旧，、维修等固定费用为3万元，每生产1万件化妆品需再投入32万元的生产费用，若将每件化妆品的售价定为：其生产成本的150%与平均每件促销费的一半之和，则当年生产的化妆品正好能销完.

(Ⅰ)将2002年的利润y(万元)表示为促销费ｔ(万元)的函数；

(Ⅱ)该企业2002年的促销费投入多少万元时，企业的年利润最大?。

(注：利润＝销售收入—生产成本—促销费，生产成本＝固定费用＋生产费用)

参考答案

一、选择题：（本大题共10小题，每小题5分，共50分）

题号	1	2	3	4	5	6	7	8	9	10
答案	B	C	A	D	C	A	C	C	A	D

二、填空题：（本题每小题4分，共24分）

11、若q则p；若非p则非q；若非q则非p；逆否命题.　　 12、必要不充分.　　

 13．5 .　　 14、3x+y＋2=0 .　　　　 15、－2 .　　　　　  16、19kg.

三、解答题：（本题共76分）

17．　　

18． 解：(1)2－≥0, 得≥0, x<－1或x≥1　即A=(－∞,－1)∪[1,+ ∞)

(2) 由(x－a－1)(2a－x)>0, 得(x－a－1)(x－2a)<0.

∵a<1,∴a+1>2a, ∴B=(2a,a+1).∵BA, ∴2a≥1或a+1≤－1, 即a≥或a≤－2, 而a<1,

∴≤a<1或a≤－2, 故当BA时, 实数a的取值范围是(－∞,－2)∪[,1] ）

20、

21、m＝n＝5　

22、解：（Ⅰ）由题意：　将

当年生产x(万件)时，年生产成本＝年生产费用＋固定费用＝32x＋3＝32（3－）＋3，

当销售x（万件）时，年销售收入＝150%［32（3－＋3］＋

由题意，生产x万件化妆品正好销完

∴年利润＝年销售收入－年生产成本－促销费

即（t≥0）

（Ⅱ）∵≤50－＝42万件当且仅当

即t＝7时，y_max＝42

∴当促销费定在7万元时，利润增大.