高中学生学科素质训练
高三数学测试题—参数方程和极坐标方程（15
一、选择题（本题每小题5分，共60分）
1．参数方程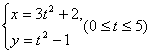
表示的曲线是 （ ）
A．线段 B．双曲线的一支 C．圆弧 D．射线
2．参数方程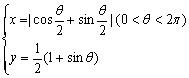
表示 （ ）
A．双曲线一支，这支过点（1，
） B．抛物线的一部分，这部分过点（1，）
C．双曲线的一支，这支过点（－1,） D．抛物线的一部分，这部分过点（－1，）
3．极坐标方程
化为直角坐标方程的形式是 （ ）
A．
B．
C．
D．
4．在极坐标系中，如果等边三角形的两个顶点是A（2，
），B（2，
），那么顶点C的
坐标可能是 （ ）
A．
B．
C．
D．(3，
)
5．已知动圆方程
为参数），那么圆心的轨迹
是 （ ）
A．椭圆 B．椭圆的一部分 C．抛物线 D．抛物线的一部分
6．已知集合
，
，下列等式成立的是（ ）
A．A=B B．B=D C．A=C D．B=C
7．点P（x，y）是曲线
上的点，则
的最大值和最小
值分别是 （ ）
A．7，－1 B．5，1 C．7，1 D．4，－1
8．实数x、y满足
的最大值是 （ ）
A．2 B．4 C．
D．5
9．曲线
和
所围成的图形的面积是 （ ）
A．
B．
C．
D．
10．直线
与圆
相切的条件是 （ ）
A．
B．
C．
D．
11．直线
的位置关系是 （ ）
A．平行 B．重合 C．垂直 D．斜交
12．已知直线l的方程
，直线
与l关于极点对称，则的方程为（ ）
A．
B．
C．
D．
二、填空题（本题每小题4分，共16分）
13．由参数方程
给出的曲线在直角坐标下的普通方程是 .
14．在满足方程
的所有实数对（x，y）中，xy的最大值为
最小值为 .
15．在极坐标系中，以
为圆心，
为半径的圆的方程为
.
16．长为3a的线段的端点分别在x、y轴上滑动，M为AB的一个三等分点，则M的轨迹方
程是 .
三、解答题（本题17—21小题每小题12分，22小题14分，共74分）
17．已知椭圆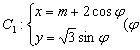
为参数）及抛物线
时，
求m的取值范围.
18．求椭圆
上的点P到直线
的最大距离及此时P点的
坐标.
19．求以y轴为准线，顶点在曲线
上的抛物线焦点的轨迹方程，并指出是什么
曲线.
20．已知
为直线
上任意一点，连O并延长至P，使O·OP=4，求P
点的轨迹.
21．已知抛物线
与圆
.
（1）求证：C1与C2无交点；
|
且AB=CD，求a的取值范围.
|
上两点，且OA⊥OB，
（1）求证
为定值；
（2）求证直线恒切于一定圆；
（3）试求
的最值.
高三数学测试题参考答
十五、参数方程和极坐标方程
一、1．A消参后，得
2. B 3. B 4. B 5. D圆心轨迹的参数方程为：
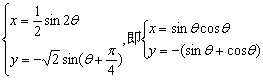，消去参数得
.
6. B集合B与D都是曲线：
7. 将原方程配方，得
令即
时
；
当
. 8．B 令
，代入
得
. 9.D 10.A 11.C 12.D
二、13．
消参可得 14． 最大值为9，最小值为1. 15．
.利用直角三角形
的边、角关系. 16．
利用定比分点坐标公式.
三、17．解：将椭圆C1的参数方程代入C2：
整理得 
也即
18．解：∵椭圆上的点
到直线的距离
当
时，
|
，∵y轴为准线，
到准线的距离为
∴焦点到准线的距离
又焦点与顶
点的横坐标同号，设焦点为（x，y），则
，消去θ，
得焦点的轨迹方程为
.表示双曲线
20．解：以原点O为极点，Ox为极轴，建立极坐标系，则直线方程化为极坐标方程为：
，
设
、
，由已知
.代入直线的极坐标方程得：
，
化为直角坐标方程：
（除去原点）.
21．解：（1）两方程联立，消去y，得
两曲线无交点.
（2）设直线
（t为参数）代入
.
则
① 且
将l的方程代入
，得
，② 且
，由
AB=CD，∴AB与BC的中点必重合，
③ 将③分别代入①和②，得：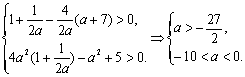
又由③
22．解（1）将椭圆
化为极坐标方程得：
设
=定值.
（2）
AOB是直角三角形. 
.过O作OH⊥AB则OH为点O到AB的距离.
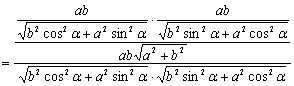
（定
值）. ∴直线AB恒切于一定圆：圆心为O（0，0），半径
，方程为
（3）由
.
时，也就是
的最大值为
. 当
或
的最小值为