素质能力检测(二)
一、选择题(每小题5分,共60分)
1.(2002年全国)函数y=x2+bx+c(x∈[0,+∞))是单调函数的充要条件是
A.b≥0 B.b≤0
C.b>0 D.b<0
解析:y=x2+bx+c的对称轴为x=-![]() ,∴-
,∴-![]() ≤0.∴b≥0.
≤0.∴b≥0.
答案:A
2.(2004年全国Ⅲ,理11)设函数f(x)=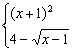
![]() 则使得f(x)≥1的自变量x的取值范围为
则使得f(x)≥1的自变量x的取值范围为
A.(-∞,-2]∪[0,10] B.(-∞,-2]∪[0,1]
C.(-∞,-2]∪[1,10] D.[-2,0]∪[1,10]
解析:当x<1时,f(x)≥1![]() (x+1)2≥1
(x+1)2≥1![]() x≤-2或x≥0,∴x≤-2或0≤x<1.
x≤-2或x≥0,∴x≤-2或0≤x<1.
当x≥1时,f(x)≥1![]() 4-
4-![]() ≥1
≥1![]()
![]() ≤3
≤3![]() 1≤x≤10.
1≤x≤10.
综上,知x≤-2或0≤x≤10.
答案:A
3.f(x)是定义在R上的奇函数,它的最小正周期为T,则f(-![]() )的值为
)的值为
A.0 B.![]() C.T D.-
C.T D.-![]()
解法一:由f(![]() )=f(-
)=f(-![]() +T)=f(-
+T)=f(-![]() )=-f(
)=-f(![]() ),知f(
),知f(![]() )=0.
)=0.
解法二:取特殊函数f(x)=sinx.
答案:A
4.(2004年上海,文15)若函数y=f(x)的图象与函数y=lg(x+1)的图象关于直线x-y=0对称,则f(x)等于
A.10x-1 B.1-10x
C.1-10-x D.10-x-1
解析:∵y=f(x)与y=lg(x+1)关于x-y=0对称,
∴y=f(x)与y=lg(x+1)互为反函数.
∴由y=lg(x+1),得x=10y-1.
∴所求y=f(x)=10x-1.
答案:A
5.函数f(x)是一个偶函数,g(x)是一个奇函数,且f(x)+g(x)=![]() ,则f(x)等于
,则f(x)等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解析:由题知f(x)+g(x)=![]() , ①
, ①
以-x代x,①式得f(-x)+g(-x)=![]() ,即f(x)-g(x)=
,即f(x)-g(x)=![]() ,
②
,
②
①+②得f(x)=![]() .
.
答案:A
6.(2004年江苏,11)设k>1,f(x)=k(x-1)(x∈R),在平面直角坐标系xOy中,函数y=f(x)的图象与x轴交于A点,它的反函数y=f-1(x)的图象与y轴交于B点,且这两个函数的图象交于P点.已知四边形OAPB的面积是3,则k等于
A.3 B.![]() C.
C.![]() D.
D.![]()
解析:用k表示出四边形OAPB的面积.
答案:B
7.F(x)=(1+![]() )·f(x)(x≠0)是偶函数,且f(x)不恒等于零,则f(x)
)·f(x)(x≠0)是偶函数,且f(x)不恒等于零,则f(x)
A.是奇函数 B.是偶函数
C.既是奇函数,又是偶函数 D.是非奇非偶函数
解析:g(x)=1+![]() 是奇函数,
是奇函数,
∴f(x)是奇函数.
答案:A
8.(2003年杭州市质检题)当a≠0时,函数y=ax+b和y=bax的图象只可能是
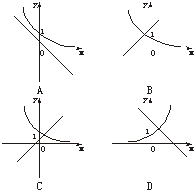
答案:C
9.(2004年全国Ⅳ,12)设函数f(x)(x∈R)为奇函数,f(1)=![]() ,f(x+2)=f(x)+
,f(x+2)=f(x)+
f(2),则f(5)等于
A.0 B.1 C.![]() D.5
D.5
解析:∵f(x+2)=f(x)+f(2)且f(x)为奇函数,f(1)=![]() ,∴f(1)=f(-1+2)=
,∴f(1)=f(-1+2)=
f(-1)+f(2)=-f(1)+f(2).∴f(2)=2f(1)=1.∴f(5)=f(3)+f(2)=f(1+2)+ f(2)=f(1)+2f(2)=![]() .
.
答案:C
10.设函数f(x)=![]() 的图象如下图所示,则a、b、c的大小关系是
的图象如下图所示,则a、b、c的大小关系是
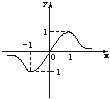
A.a>b>c B.a>c>b C.b>a>c D.c>a>b
解析:f(0)=![]() =0,∴b=0.
=0,∴b=0.
f(1)=1,∴![]() =1.
=1.
∴a=c+1.由图象看出x>0时,f(x)>0,即x>0时,有![]() >0,∴a>0.又f(x)=
>0,∴a>0.又f(x)= ![]() ,当x>0时,要使f(x)在x=1时取最大值1,需x+
,当x>0时,要使f(x)在x=1时取最大值1,需x+![]() ≥2
≥2![]() ,当且仅当x=
,当且仅当x=![]() =1时.∴c=1,此时应有f(x)=
=1时.∴c=1,此时应有f(x)=![]() =1.
=1.
∴a=2.
答案:B
11.偶函数y=f(x)(x∈R)在x<0时是增函数,若x1<0,x2>0且x1<x2,下列结论正确的是
A.f(-x1)<f(-x2) B.f(-x1)>f(-x2)
C.f(-x1)=f(-x2) D.f(-x1)与f(-x2)大小关系不确定
解析:x越小,f(x)越大.∵x1<x2,∴选B.
答案:B
12.方程log2(x+4)=3x实根的个数是
A.0 B.1 C.2 D.3
解析:设y=log2(x+4)及y=3x.
画图知交点有两个.
答案:C
二、填空题(每小题4分,共16分)
13.(2004年浙江,理13)已知f(x)=![]() 则不等式x+(x+2)·f(x+2)≤5的解集是___________________.
则不等式x+(x+2)·f(x+2)≤5的解集是___________________.
解析:当x+2≥0时,原不等式![]() x+(x+2)≤5
x+(x+2)≤5![]() x≤
x≤![]() .∴-2≤x≤
.∴-2≤x≤![]() .
.
当x+2<0时,原不等式![]() x+(x+2)(-1)≤5
x+(x+2)(-1)≤5![]() -2≤5.∴x<-2.
-2≤5.∴x<-2.
综上,知x≤![]() .
.
答案:(-∞,![]() ]
]
14.设函数f(x)的定义域是N*,且f(x+y)=f(x)+f(y)+xy,f(1)=1,则f(25)= ___________________.
解析:由f(x+y)=f(x)+f(y)+xy![]() f(2)=f(1)+f(1)+1=3.
f(2)=f(1)+f(1)+1=3.
∴f(2)-f(1)=2.
同理,f(3)-f(2)=3.
……
f(25)-f(24)=25.
∴f(25)=1+2+3+…+25=325.
答案:325
15.(2004年春季上海)已知函数f(x)=log3(![]() +2),则方程f-1(x)=4的解x=___________________.
+2),则方程f-1(x)=4的解x=___________________.
解析:由f-1(x)=4,得x=f(4)=log3(![]() +2)=1.
+2)=1.
答案:1
16.对于函数y=f(x)(x∈R),有下列命题:
①在同一坐标系中,函数y=f(1+x)与y=f(1-x)的图象关于直线x=1对称;
②若f(1+x)=f(1-x),且f(2-x)=f(2+x)均成立,则f(x)为偶函数;
③若f(x-1)=f(x+1)恒成立,则y=f(x)为周期函数;
④若f(x)为单调增函数,则y=f(ax)(a>0,且a≠1)也为单调增函数.
其中正确命题的序号是______________.
(注:把你认为正确命题的序号都填上)
解析:①不正确,y=f(x-1)与y=f(1-x)关于直线x=1对称.②正确.③正确.④不正确.
答案:②③
三、解答题(共6小题,满分74分)
17.(12分)函数y=lg(3-4x+x2)的定义域为M,x∈M时,求f(x)=2x+2-3×4x的最值.
解:由3-4x+x2>0得x>3或x<1,
∴M={xx>3或x<1},
f(x)=-3×22x+22·2x=-3(2x-![]() )2+
)2+![]() .
.
∵x>3或x<1,
∴2x>8或0<2x<2.
∴当2x=![]() 即x=log2
即x=log2![]() 时,f(x)最大,最大值为
时,f(x)最大,最大值为![]() .
.
f(x)没有最小值.
18.(12分)(2003年高考新课程卷)设a>0,求函数f(x)=![]() -ln(x+a)(x∈(0,+∞))的单调区间.
-ln(x+a)(x∈(0,+∞))的单调区间.
分析:本小题主要考查导数的概念和计算,应用导数研究函数性质的方法及推理和运算能力.
解:![]() (x)=
(x)=![]() -
-![]() (x>0).
(x>0).
当a>0,x>0时,
![]() (x)>0
(x)>0![]() x2+(2a-4)x+a2>0,
x2+(2a-4)x+a2>0,
![]() (x)<0
(x)<0![]() x2+(2a-4)x+a2<0.
x2+(2a-4)x+a2<0.
①当a>1时,对所有x>0,有x2+(2a-4)x+a2>0,即![]() (x)>0.
(x)>0.
此时f(x)在(0,+∞)内单调递增.
②当a=1时,对x≠1,有x2+(2a-4)x+a2>0,
即![]() (x)>0,此时f(x)在(0,1)内单调递增,在(1,+∞)内单调递增.
(x)>0,此时f(x)在(0,1)内单调递增,在(1,+∞)内单调递增.
又知函数f(x)在x=1处连续.
因此,函数f(x)在(0,+∞)内单调递增.
③当0<a<1时,令![]() (x)>0,即
(x)>0,即
x2+(2a-4)x+a2>0,解得x<2-a-2![]() ,或x>2-a+2
,或x>2-a+2![]() .
.
因此,函数f(x)在区间(0,2-a-2![]() )内单调递增,在区间(2-a+2
)内单调递增,在区间(2-a+2![]() ,+∞)内也单调递增.
,+∞)内也单调递增.
令![]() (x)<0,即x2+(2a-4)x+a2<0,解得2-a-2
(x)<0,即x2+(2a-4)x+a2<0,解得2-a-2![]() <x<2-a+2
<x<2-a+2![]() .
.
因此,函数f(x)在区间(2-a-2![]() ,2-a+2
,2-a+2![]() )内单调递减.
)内单调递减.
19.(12分)(2005年春季北京,理20)现有一组互不相同且从小到大排列的数据:a0,a1,a2,a3,a4,a5,其中a0=0.为提取反映数据间差异程度的某种指标,今对其进行如下加工:记T=a0+a1+…+a5,xn=![]() ,yn=
,yn=![]() (a0+a1+…+an),作函数y=f(x),使其图象为逐点依次连结点Pn(xn,yn)(n=0,1,2,…,5)的折线.
(a0+a1+…+an),作函数y=f(x),使其图象为逐点依次连结点Pn(xn,yn)(n=0,1,2,…,5)的折线.
(1)求f(0)和f(5)的值;
(2)设Pn-1Pn的斜率为kn(n=1,2,3,4,5),判断k1、k2、k3、k4、k5的大小关系;
(3)证明f(xn)<xn(n=1,2,3,4).
(1)解:f(0)=![]() =0,
=0,
f(5)=![]() =1.
=1.
(2)解:kn=![]() =
=![]() an,n=1,2,…,5.
an,n=1,2,…,5.
因为a1<a2<a3<a4<a5,
所以k1<k2<k3<k4<k5.
(3)证法一:对任何n(n=1,2,3,4),
5(a1+…+an)=[n+(5-n)](a1+…+an)
=n(a1+…+an)+(5-n)(a1+…+an)
≤n(a1+…+an)+(5-n)nan
=n[a1+…+an+(5-n)an]
<n(a1+…+an+an+1+…+a5)=nT,
所以f(xn)=![]() <
<![]() =xn.
=xn.
证法二:对任何n(n=1,2,3,4),
当kn<1时,
yn=(y1-y0)+(y2-y1)+…+(yn-yn-1)
=![]() (k1+k2+…+kn)<
(k1+k2+…+kn)<![]() =xn.
=xn.
当kn≥1时,
yn=y5-(y5-yn)
=1-[(yn+1-yn)+(yn+2-yn+1)+…+(y5-y4)]
=1-![]() (kn+1+kn+2+…+k5)<1-
(kn+1+kn+2+…+k5)<1-![]() (5-n)=
(5-n)=![]() =xn,
=xn,
综上,f(xn)<xn.
20.(12分)(2003年北京)有三个新兴城镇,分别位于A、B、C三点处,且AB=AC=a,BC=2b.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处.(建立坐标系如下图)
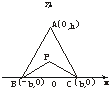
(1)若希望点P到三镇距离的平方和为最小,点P应位于何处?
(2)若希望点P到三镇的最远距离为最小,点P应位于何处?
分析:本小题主要考查函数、不等式等基本知识,考查运用数学知识分析问题和解决问题的能力.
(1)解:由题设可知,a>b>0,记h=![]() ,设P的坐标为(0,y),则P至三镇距离的平方和为
,设P的坐标为(0,y),则P至三镇距离的平方和为
f(y)=2(b2+y2)+(h-y)2=3(y-![]() )2+
)2+![]() h2+2b2.
h2+2b2.
∴当y=![]() 时,函数f(y)取得最小值.
时,函数f(y)取得最小值.
∴点P的坐标是(0,![]()
![]() ).
).
(2)解法一:P至三镇的最远距离为
g(y)=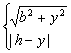
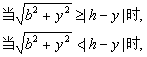
由![]() ≥h-y解得y≥
≥h-y解得y≥![]() ,记y*=
,记y*=![]() ,于是
,于是
g(y)=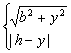
![]()
当y*=![]() ≥0,即h≥b时,
≥0,即h≥b时,![]() 在[y*,+∞)上是增函数,而h-y在(-∞,y*)上是减函数,由此可知,当y=y*时,函数g(y)取得最小值;
在[y*,+∞)上是增函数,而h-y在(-∞,y*)上是减函数,由此可知,当y=y*时,函数g(y)取得最小值;
当y*=![]() <0,即h<b时,函数
<0,即h<b时,函数![]() 在[y*,+∞)上,当y=0时,取得最小值b,而h-y在(-∞,y*)上为减函数,且h-y>b.可见,当y=0时,函数g(y)取得最小值.
在[y*,+∞)上,当y=0时,取得最小值b,而h-y在(-∞,y*)上为减函数,且h-y>b.可见,当y=0时,函数g(y)取得最小值.
∴当h≥b时,点P的坐标为(0,![]() );
);
当h<b时,点P的坐标为(0,0).其中h=![]() .
.
解法二:P至三镇的最远距离为
g(y)=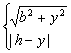
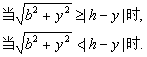
由![]() ≥h-y解得y≥
≥h-y解得y≥![]() ,记y*=
,记y*=![]() ,于是
,于是
g(y)=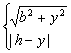
![]()
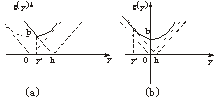
当y*≥0,即h≥b时,z=g(y)的图象如图(a),因此,当y=y*时,函数g(y)取得最小值.
当y*<0,即h<b时,z=g(y)的图象如图(b),因此,当y=0时,函数g(y)取得最小值.
∴当h≥b时,点P的坐标为(0,![]() );
);
当h<b时,点P的坐标为(0,0).其中h=![]() .
.
解法三:∵在△ABC中,AB=AC=a,
∴△ABC的外心M在射线AO上,其坐标为(0,![]() ),且AM=BM=CM.
),且AM=BM=CM.
当P在射线MA上,记P为P1;
当P在射线MA的反向延长线上,记P为P2.
若h=![]() ≥b〔如图(c)〕,
≥b〔如图(c)〕,
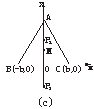
则点M在线段AO上.
这时P到A、B、C三点的最远距离为P1C或P2A,且P1C≥MC,P2A≥MA,
所以点P与外心M重合时,P到三镇的最远距离最小.
若h=![]() <b〔如图(d)〕,则点M在线段AO外.
<b〔如图(d)〕,则点M在线段AO外.
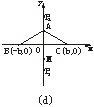
这时P到A、B、C三点的最远距离为P1C或P2A,且P1C≥OC,P2A≥OC,所以点P与BC边的中点O重合时,P到三镇的最远距离最小.
∴当![]() ≥b时,点P的位置在△ABC的外心(0,
≥b时,点P的位置在△ABC的外心(0,![]() );
);
当![]() <b时,点P的位置在原点O.
<b时,点P的位置在原点O.
21.(12分)设f(x)是定义在R上的偶函数,其图象关于直线x=1对称,对任意x1、x2∈[0,![]() ],都有f(x1+x2)=f(x1)·f(x2).
],都有f(x1+x2)=f(x1)·f(x2).
(1)设f(1)=2,求f(![]() ),f(
),f(![]() );
);
(2)证明f(x)是周期函数.
(1)解:由f(x1+x2)=f(x1)·f(x2),x1、x2∈[0,![]() ]知f(x)=f(
]知f(x)=f(![]() )·f(
)·f(![]() )=[f(
)=[f(![]() )]2≥0,x∈[0,1].
)]2≥0,x∈[0,1].
因为f(1)=f(![]() )·f(
)·f(![]() )=[f(
)=[f(![]() )]2,及f(1)=2,所以f(
)]2,及f(1)=2,所以f(![]() )=2
)=2![]() .
.
因为f(![]() )=f(
)=f(![]() )·f(
)·f(![]() )=[f(
)=[f(![]() )]2,及f(
)]2,及f(![]() )=2
)=2![]() ,所以f(
,所以f(![]() )=2
)=2![]() .
.
(2)证明:依题设y=f(x)关于直线x=1对称,故f(x)=f(1+1-x)![]() f(x)=
f(x)=
f(2-x),x∈R.
又由f(x)是偶函数知f(-x)=f(x),x∈R,所以f(-x)=f(2-x),x∈R.将上式中-x以x代换,得f(x)=f(x+2),x∈R.
这表明f(x)是R上的周期函数,且2是它的一个周期.
22.(14分)设函数y=f(x)定义在R上,对任意实数m、n,恒有f(m+n)=f(m)·
f(n)且当x>0时,0<f(x)<1.
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减;
(3)设集合A={(x,y)f(x2)·f(y2)>f(1)},B={(x,y)f(ax-y+2)=1,
a∈R},若A∩B=![]() ,求a的取值范围.
,求a的取值范围.
(1)证明:在f(m+n)=f(m)f(n)中,
令m=1,n=0,得f(1)=f(1)f(0).
∵0<f(1)<1,∴f(0)=1.
设x<0,则-x>0.令m=x,n=-x,代入条件式有f(0)=f(x)·f(-x),而f(0)=1,
∴f(x)=![]() >1.
>1.
(2)证明:设x1<x2,则x2-x1>0,
∴0<f(x2-x1)<1.
令m=x1,m+n=x2,
则n=x2-x1,代入条件式,得
f(x2)=f(x1)·f(x2-x1),
即0<![]() <1.∴f(x2)<f(x1).
<1.∴f(x2)<f(x1).
∴f(x)在R上单调递减.
(3)解:由f(x2)·f(y2)>f(1)![]() f(x2+y2)>f(1).
f(x2+y2)>f(1).
又由(2)知f(x)为R上的减函数,
∴x2+y2<1![]() 点集A表示圆x2+y2=1的内部.
点集A表示圆x2+y2=1的内部.
由f(ax-y+2)=1得ax-y+2=0![]() 点集B表示直线ax-y+2=0.
点集B表示直线ax-y+2=0.
∵A∩B=![]() ,∴直线ax-y+2=0与圆x2+y2=1相离或相切.
,∴直线ax-y+2=0与圆x2+y2=1相离或相切.
于是![]() ≥1
≥1![]() -
-![]() ≤a≤
≤a≤![]() .
.