素质能力检测(五)
一、选择题(每小题5分,共60分)
1.点M(4,-3)关于点N(5,-6)的对称点是
A.(4,3) B.(![]() ,0)
,0)
C.(-![]() ,3) D.(6,-9)
,3) D.(6,-9)
解析:设M关于N的对称点为![]() (x,y),
(x,y),![]() =
=![]() ,把坐标代入即可.
,把坐标代入即可.
答案:D
2.有三个命题:①向量![]() 与
与![]() 是共线向量,则A、B、C、D必在同一直线上;②向量a与向量b平行,则a与b的方向相同或相反;③四边形ABCD是平行四边形的充要条件是
是共线向量,则A、B、C、D必在同一直线上;②向量a与向量b平行,则a与b的方向相同或相反;③四边形ABCD是平行四边形的充要条件是![]() =
=![]() .其中正确的是
.其中正确的是
A.② B.③ C.①③ D.②③
解析:①![]() 与
与![]() 共线,AB与CD也可以平行.②中a与b也可能为0.选B.
共线,AB与CD也可以平行.②中a与b也可能为0.选B.
答案:B
3.已知A(1,2),B(4,2),则向量![]() 按向量a=(-1,3)平移后得到的向量坐标是
按向量a=(-1,3)平移后得到的向量坐标是
A.(3,0) B.(3,5)
C.(-4,3) D.(2,3)
解析:![]() =(3,0),向量
=(3,0),向量![]() 按任何方向平移后坐标不变.
按任何方向平移后坐标不变.
答案:A
4.已知a=4,b=8且a与2b-a互相垂直,则向量a与b的夹角是
A.arccos![]() B.π-arccos
B.π-arccos![]()
C.![]() D.
D.![]()
解析:由a⊥(2b-a)得a·(2b-a)=0,∴2abcosθ-a2=0.∴cosθ=![]() .
.
又0≤θ≤π,∴θ=arccos![]() .
.
答案:A
5.△ABC中,已知b=10,c=15,C=30°,则此三角形的解的情况是
A.一解 B.两解 C.无解 D.无法确定
解析:由b<c得B<C,B必为小于30°的锐角.
答案:A
6.下列命题:
①k∈R,且kb=0,则k=0或b=0;
②若a·b=0,则a=0或b=0;
③若不平行的两个非零向量a、b,满足a=b,则(a+b)·(a-b)=0;
④若a与b平行,则a·b=ab;
⑤a∥b,b∥c,则a∥c.
其中真命题的个数是
A.1 B.2 C.3 D.4
解析:①正确;②错误,若a⊥b,则a·b=0;③正确,因为(a+b)·(a-b)=a2-b2=0;④正确,可设a=λb,则a·b=λb·b=λb2;⑤错误,若b=0,则对任意a与c,均有a∥b,b∥c成立.
答案:C
7.已知点P(cosα,sinα),Q(cosβ,sinβ),则![]() 的最大值是
的最大值是
A.![]() B.2 C.4 D.不存在
B.2 C.4 D.不存在
解析:PQ2=(cosβ-cosα)2+(sinβ-sinα)2=2-2(cosαcosβ+sinαsinβ)=
2-2cos(α-β),故当cos(α-β)=-1时,PQ取最大值2.
答案:B
8.在△ABC中,a2+b2-c2=ab,则角C为
A.60° B.45°或135°
C.120° D.30°
解析:cosC=![]() =
=![]() ,C=60°.
,C=60°.
答案:A
9.点P1,P2,…,Pn是线段AB的n个n+1等分点,P∈{P1,P2,…,Pn},则P分有向线段![]() 的比λ的最大值和最小值分别是
的比λ的最大值和最小值分别是
A.n+1,![]() B.n+1,
B.n+1,![]()
C.n,![]() D.n-1,
D.n-1,![]()
解析:由![]() =λ
=λ![]() 知λ取得最大值时P为距点B最近的点Pn,取最小值时为P1.
知λ取得最大值时P为距点B最近的点Pn,取最小值时为P1.
答案:C
10.若a与b的夹角为60°,b=2,(a+b)·(a-2b)=-2,则向量a的模是
A.2 B.5 C.3 D.6
解析:由题意知a2-a·b-2b2=-2,b=2,cos60°=![]() ,代入得a2-a-6=0.
,代入得a2-a-6=0.
∴a=3或a=-2(舍去).
答案:C
11.命题p:a=b且a∥b;命题q:a=b,则p是q的
A.充分不必要条件 B.必要不充分要件
C.充分必要条件 D.既不充分又不必要条件
解析:当a∥b且a与b方向相反时,即使a=b,也不能得到a=b,故a=b且a∥b不是a=b的充分条件,而是必要不充分条件.
答案:B
12.在平面直角坐标系中,O为原点,OA=a,![]() =b,对任意一点M,它关于A的对称点为S,S关于点B的对称点为N,则
=b,对任意一点M,它关于A的对称点为S,S关于点B的对称点为N,则![]() 用a、b表示为
用a、b表示为
A.2(b-a) B.![]() (a-b)
(a-b)
C.a+b D.![]() (a+b)
(a+b)
解析:![]() =
=![]() +
+![]() =2
=2![]() +2
+2![]() =2
=2![]() -2
-2![]() .(四边形OASB是平行四边形)
.(四边形OASB是平行四边形)
答案:A
二、填空题(每小题4分,共16分)
13. ![]() =3e1,
=3e1,![]() =3e2,且
=3e2,且![]() =
=![]()
![]() ,则
,则![]() =____________.
=____________.
解析:![]() =3e2-3e1,
=3e2-3e1,![]() =
=![]()
![]() =e2-e1,
=e2-e1,![]() =
=![]() +
+![]() =2e1+e2.
=2e1+e2.
答案:2e1+e2
14.已知向量a=(1,![]() ),b=(-
),b=(-![]() ,1),若正数k和t满足x=a+(t2+1)b与y=-ka+
,1),若正数k和t满足x=a+(t2+1)b与y=-ka+![]() b垂直,则k的最小值是____________.
b垂直,则k的最小值是____________.
解析:x=(1-![]() -
-![]() t2,1+
t2,1+![]() +t2),y=(-k-
+t2),y=(-k-![]() ,-
,-![]() k+
k+![]() ),由x⊥y得x·y=0.又t>0,∴k=t+
),由x⊥y得x·y=0.又t>0,∴k=t+![]() ≥2.∴当t=1时,k的最小值为2.
≥2.∴当t=1时,k的最小值为2.
答案:2
15.在△ABC中,记BC=a,AC=b,AB=c,若9a2+9b2-19c2=0,则![]() =____________.
=____________.
解析:![]() =
=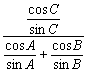
=![]() =
=![]() =
=![]()
=![]()
=![]() =
=![]() .
.
答案:![]()
16.已知直线l1过点(0,t),方向向量为(1,1),直线l2过点(t,1),方向向量为(1,-2),P为l1、l2的交点,当t变化时,P的轨迹方程为____________.
解析:l1方程为x-y+t=0,l2方程为2x+y-1-2t=0,两式消去t即得P的轨迹方程.
答案:4x-y-1=0
三、解答题(本大题共6小题,共74分)
17.(12分)已知向量a=(3,-4),求:
(1)与a平行的单位向量b;
(2)与a垂直的单位向量c;
(3)将a绕原点逆时针方向旋转45°得到的向量e的坐标.
解:(1)设b=λa,则b=1,b=(![]() ,-
,-![]() )或b=(-
)或b=(-![]() ,
,![]() ).
).
(2)由a⊥c,a=(3,-4),可设c=λ(4,3),求得c=(![]() ,
,![]() )或c=(-
)或c=(-![]() ,-
,-![]() ).
).
(3)设e=(x,y),则x2+y2=25.
又a·e=3x-4y=aecos45°,即3x-4y=![]() ,由上面关系求得e=(
,由上面关系求得e=(![]() ,-
,-![]() ),或e=(-
),或e=(-![]() ,-
,-![]() ),
),
而向量e由a绕原点逆时针方向旋转45°得到,故e=(![]() ,-
,-![]() ).
).
18.(12分)向量a=(1,cos2θ),b=(2,1),c=(4sinθ,1),d=(![]() sinθ,1),其中θ∈(0,
sinθ,1),其中θ∈(0,![]() ).
).
(1)求a·b-c·d的取值范围;
(2)若函数f(x)=x-1,判断f(a·b)与f(c·d)的大小,并说明理由.
解:(1)a·b=2+cos2θ,c·d=2sin2θ+1=2-cos2θ.
∵a·b-c·d=2cos2θ,
∴0<θ<![]() .∴0<2θ<
.∴0<2θ<![]() .
.
∴0<cos2θ<1.∴0<2cos2θ<2.
∴a·b-c·d的取值范围是(0,2).
(2)f(a·b)=2+cos2θ-1=1+cos2θ=2cos2θ,
f(c·d)=2-cos2θ-1=1-cos2θ=2sin2θ.
于是有f(a·b)-f(c·d)=2(cos2θ-sin2θ)=2cos2θ.
∵0<θ<![]() ,∴0<2θ<
,∴0<2θ<![]() .
.
∴2cos2θ>0.∴f(a·b)>f(c·d).
19.(12分)△ABC的三个内角A、B、C满足下列条件:
①A<B<C;②A、B、C成等差数列;③tanA·tanC=2+![]() .
.
(1)求A、B、C的大小;
(2)若AB边上的高为4![]() ,求a、b、c的大小.
,求a、b、c的大小.
解:(1)由题意知B=60°,A+C=120°,tan(A+C)=![]() =-tanB=-
=-tanB=-![]() ,∴tanA+tanC=3+
,∴tanA+tanC=3+![]() .故
.故![]() 或
或![]() (舍),故A=45°,B=60°,C=75°.
(舍),故A=45°,B=60°,C=75°.
(2)过C作CD⊥AB于点D,则CD=4![]() ,在Rt△ACD和Rt△ABC中,由正弦定理得a=
,在Rt△ACD和Rt△ABC中,由正弦定理得a=![]() =8,b=
=8,b=![]() =4
=4![]() ,c=AD+DB=4
,c=AD+DB=4![]() +4.
+4.
20.(12分)已知a=(cosθ,sinθ),b=(cosβ,sinβ),a与b之间有关系式ka+b=![]() a-kb(k>0).
a-kb(k>0).
(1)用k表示a·b;
(2)求a·b的最小值,并求此时a与b夹角的大小.
解:(1)将ka+b=![]() a-kb两边平方得a·b=
a-kb两边平方得a·b=![]() =
=![]() .
.
(2)∵(k-1)2≥0,
又k>0,∴![]() ≥
≥![]() =
=![]() ,
,
即a·b≥![]() ,cosα=
,cosα=![]() .
.
又0°≤α≤180°,故a与b的夹角为60°.
21.(12分)已知矩形ABCD,E、F分别是AD、BC的中点,求证:对角线AC⊥BE,AC⊥DF的充要条件是AB∶BC=1∶![]() .
.
证明:设![]() =a,
=a,![]() =b,则a⊥b.
=b,则a⊥b.
![]() =
=![]() b,
b,![]() =b-a,
=b-a,![]() =
=![]() +
+![]() =a+
=a+![]() b.
b.
(1)必要性:∵![]() ⊥
⊥![]() ,∴(b-a)·(a+
,∴(b-a)·(a+![]() b)=0,
b)=0,
即a·b+![]() b2-a2-
b2-a2-![]() a·b=0.
a·b=0.
∵a⊥b,∴a·b=0.
∴![]() b2-a2=0,即
b2-a2=0,即![]() b2=a2,得b2=2a2,b=
b2=a2,得b2=2a2,b=![]() a.
a.
∴AB∶BC=1∶![]() .
.
(2)充分性:∵![]() ·
·![]() =(b-a)·(a-
=(b-a)·(a-![]() b)=a·b+
b)=a·b+![]() b2-a2-
b2-a2-![]() a·b,
a·b,
又∵a⊥b,∴a·b=0.
∴![]() ·
·![]() =
=![]() b2-a2=
b2-a2=![]() b2-a2.
b2-a2.
∵AB∶BC=1∶![]() ,∴a∶b=1∶
,∴a∶b=1∶![]() .
.
∴a2=![]() b2.∴
b2.∴![]() ·
·![]() =0.
=0.
故![]() ⊥
⊥![]() .
.
同理可证![]() ·
·![]() =0,则
=0,则![]() ⊥
⊥![]() .
.
综合(1)(2)知AC⊥BE,AC⊥DF的充要条件是AB∶BC=1∶![]() .
.
22.(14分)设坐标平面上全部向量的集合为V,a=(a1,a2)为V的一个单位向量.已知从V到V的映射f由f(x)=-x+2(x·a)a(x∈V)确定.
(1)若x、y∈V,求证:f(x)·f(y)=x·y;
(2)对于x∈V,计算f[f(x)]-x;
(3)设u=(1,0),v=(0,1),若f(u)=v,求a.
(1)证明:f(x)·f(y)=[-x+2(x·a)a]·[-y+2(y·a)a]
=x·y-4(x·a)(y·a)+4(x·a)(y·a)a2=x·y.
(2)解:∵f[f(x)]=f[-x+2(x·a)a]
=-[-x+2(x·a)a]+2{[-x+2(x·a)a]·a}a
=x-2(x·a)a+2[-x·a+2(x·a)a2]a
=x-2(x·a)a+2(x·a)a=x,
∴f[f(x)]-x=0.
(3)解:由f(u)=v,得![]()
解得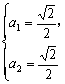 或
或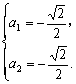
∴a=(![]() ,
,![]() )或a=(-
)或a=(-![]() ,-
,-![]() ).
).