高考第一轮复习数学：三角函数（附答案）

素质能力检测（四）

一、选择题（每小题6分，共60分）

1.（2004年辽宁，1）若cosθ＞0，且sin2θ＜0，则角θ的终边所在象限是

A.第一象限　　　　　　　　　　　　　　　　　　　　　　　　　　 B.第二象限

C.第三象限　　　　　　　　　　　　　　　　　　　　　　　　　　 D.第四象限

解析：由sin2θ＜0得2sinθcosθ＜0.又cosθ＞0，∴sinθ＜0.∴角θ的终边在第四象限.

答案：D

2.要得到函数y=sin2x的图象可由函数y=cos2x的图象

A.向左平移个单位　　　　　　　　　　　　　　　　　　　B.向右平移个单位

C.向左平移个单位　　　　　　　　　　　　　　　　　　　D.向右平移个单位

解析：y=sin2x=cos（－2x）=cos［2（x－）］.

答案：D

3.已知函数y=Asin（ωx+）在同一周期内，当x=时，取得最大值，当x=时，取得最小值－，则该函数的解析式为

A.y=2sin（－）　　　　　　　　　　　　　　　　　　　 B.y=sin（3x+）

C.y=sin（3x－）　　　　　　　　　　　　　　　　　　　D.y=sin（－）

解析：A=，=，ω==3，易知第一个零点为（－，0），则y=sin［3（x+）］，即y=sin（3x+）.

答案：B

4.设集合M={yy=sinx}，N={yy=cosxtanx}，则M、N的关系是

A.NM　　　　　　　　　　　　B.MN　　　　　　　　　　　　C.M=N　　　　　　　　　　　　 D.M∩N=

解析：M={y－1≤y≤1}，N={y－1＜y＜1}，选A.

答案：A

5.y=的值域是

A.［－1，1］　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.［－，］

C.［－，1］　　　　　　　　　　　　　　　　　　　　　　 D.［－1，］

解析：原式可化为sinx+ycosx=2y，

sin（x+）=2y（tan=），

sin（x+）=∈［－1，1］，

解得y∈［－1，1］.

答案：A

6.在△ABC中，tanA·tanB＞1，则△ABC为

A.直角三角形　　　　　　　　　　　　　　　　　　　　　　　　　　　　B.锐角三角形

C.钝角三角形　　　　　　　　　　　　　　　　　　　　　　　　　　　　D.等腰三角形

解析：tan（A+B）=－tanC，得=－tanC.∵tanA·tanB＞1，∴tanA＞0，tanB＞0.1－tanA·tanB＜0，∴－tanC＜0.tanC＞0，∴△ABC为锐角三角形.故选B.

答案：B

7.方程cosx=lgx的实根个数为

A.1个　　　　　　　　　　　　　B.2个　　　　　　　　　　　　　C.3个　　　　　　　　　　　　　D.无数个

解析：当x=10时，lgx=1，在同一坐标系中画出y=cosx和y=lgx的图象，可知有3个交点，选C.

答案：C

8.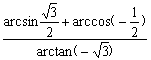的值是

A.－3　　　　　　　　　　　　　 B.2　　　　　　　　　　　　　　　C.－　　　　　　　　　　　　D.

解析：原式=－3，选A.

答案：A

9.已知f（sinx）=sin3x，则f（cosx）等于

A.－cos3x　　　　　　　　　　B.cos3x　　　　　　　　　　　　C.sin3x　　　　　　　　　　　　 D.－sin3x

解析：f（cosx）=f［sin（－x）］=sin3（－x）=－cos3x，选A.

答案：A

10.函数f（x）=sin2x+5sin（+x）+3的最小值是

A.－3　　　　　　　　　　　　　 B.－6　　　　　　　　　　　　　 C.　　　　　　　　　　　　　　　　　 D.－1

解析：f（x）=2sinxcosx+（sinx+cosx）+3.令t=sinx+cosx，t∈［－，］，则y=（t+）²－.则当t=－时，y_min=－1，选D.

答案：D

二、填空题（每小题4分，共16分）

11.已知角α的终边上一点P（，－1），则sec²α+csc²α+cot²α=_________.

解析：secα=，cscα=－2，cotα=－，代入得.

答案：

12.（2005年春季上海，11）函数y=sinx+arcsinx的值域是____________.

解析：该函数的定义域为［－1，1］.

∵y=sinx与y=arcsinx都是［－1，1］上的增函数，

∴当x=－1时，y_min=sin（－1）+arcsin（－1）=－－sin1，

当x=1时，y_max=sin1+arcsin1=+sin1，

∴值域为［－－sin1，+sin1］.

答案：［－－sin1，+sin1］

13.△ABC中，若sinA=，cosB=，则cosC=_______.

解析：由cosB=，得sinB=＞=sinA.A是锐角，cosA=，cosC=cos（π－A－B）=.

答案：

14.若f（x）=asin³x+btanx+1且f（3）=5，则f（－3）=_______.

解析：令g（x）=asin³x+btanx，则g（－x）=－g（x）.

f（3）=g（3）+1=5，g（3）=4.

f（－3）=g（－3）+1=－g（3）+1=－4+1=－3.

答案：－3

三、解答题（本大题共6小题，共74分）

15.（12分）（2005年黄冈市调研题）已知sin－cos=，α∈（，π），tan（π－β）=，求tan（α－2β）的值.

解：∵sin－cos=，

∴1－sinα=.∴sinα=.

又∵α∈（，π），∴cosα=－=－.

∴tanα=－.

由条件知tanβ=－，

∴tan2β==－.

∴tan（α－2β）==.

16.（12分）已知2cos2α－cos2β=1，求sin²2α+sin²β+2cos⁴α的值.

解：由2cos2α－cos2β=1，即2cos2α=1+cos2β，得cos2α=cos²β.因此sin²2α+sin²β+2cos⁴α=sin²2α+sin²β+2·（）²=1+cos2α+sin²β=1+cos²β+sin²β=2.

17.（12分）（2004年浙江，理17）在△ABC中，角A、B、C所对的边分别为a、b、c，且cosA=.

（1）求sin²+cos2A的值；

（2）若a=，求bc的最大值.

解：（1）sin²+cos2A=［1－cos（B+C）］+（2cos²A－1）=（1+cosA）+（2cos²A－1）=（1+）+（－1）=－.

（2）∵=cosA=，

∴bc=b²+c²－a²≥2bc－a².

∴bc≤a².

又∵a=，∴bc≤.

当且仅当b=c=时，bc=.故bc的最大值是.

18.（12分）已知a₁=，a_n+1=a_ncosx－sinnx，求a₂、a₃、a₄，推测a_n并证明.

解：a₂=a₁cosx－sinx==，a₃=a₂cosx－sin2x=，a₄=.

可推测a_n=，数学归纳法可证之.（读者自己完成）

19.（12分）设A、B、C是三角形的内角，且lgsinA=0，又sinB、sinC是关于x的方程4x²－2（+1）x+k=0的两个根，求实数k的值.

解：由lgsinA=0，得sinA=1，A=，B+C=，sinC=cosB.

又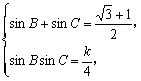

∴

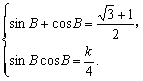
由sinBcosB=［（sinB+cosB）²－1］，得=［（）²－1］，解得k=.

20.（14分）已知F（θ）=cos²θ+cos²（θ+α）+cos²（θ+β），问是否存在满足0≤α＜β≤π的α、β，使得F（θ）的值不随θ的变化而变化?如果存在，求出α、β的值；如果不存在，请说明理由.

解：F（θ）=+［cos2θ+cos（2θ+2α）+cos（2θ+2β）］=+（1+cos2α+cos2β）cos2θ－（sin2α+sin2β）sin2θ.

F（θ）的值不随θ变化的充要条件是

得（cos2α+1）²+sin²2α=1，

cos2α=－.同理，cos2β=－.

又0≤α＜β≤π，

故存在α、β满足条件，其值分别为α=，β=.

●意犹未尽

相信自己是一只雄鹰

一个人在高山之巅的鹰巢里，抓到了一只幼鹰，他把幼鹰带回家，养在鸡笼里.这只幼鹰和鸡一起啄食、嬉闹和休息.它以为自己是一只鸡.这只鹰渐渐长大，羽翼丰满了，主人想把它训练成猎鹰，可是由于终日和鸡混在一起，它已经变得和鸡完全一样，根本没有飞的愿望了.主人试了各种办法，都毫无效果，最后把它带到山顶上，一把将它扔了出去.这只鹰像块石头似的，直掉下去，慌乱之中它拼命地扑打翅膀，就这样，它终于飞了起来！

一语中的：磨炼召唤成功的力量.