素质能力检测（十二）
一、选择题（每小题5分，共60分）
1.从50件产品中，采用逐一抽取的方法抽取5件产品，若其中只有一件次品，在送质检部门进行检验时次品被抽到的概率是
A.0.1 B.0.02
C.0或1 D.以上都不对
解析：次品被抽到的概率，即入样的概率p=
=
=0.1.
答案：A
2.某校有40个班级，每班50人，每班选派3人参加“学代会”，在这个问题中样本容量是
A.40 B.50
C.120 D.150
解析：3×40=120.
答案：C
3.从N个编号中要抽n个号码入样，考虑采用系统抽样方法，抽样距（间距）为
A.
B.n
C.［］
D.［］+1
解析：抽样间距应为的整数部分即［］.
答案：C
4.某养鸡场养有蛋鸡、肉鸡和草鸡三种鸡，其中有蛋鸡1500只，肉鸡3000只，草鸡900只，估计产量时，应采用的抽样方法是
A.分层抽样 B.随机抽样
C.系统抽样 D.以上三种方法都可以
解析：由于个体之间差异较大，故采用分层抽样.
答案：A
5.某校高三年级的195名学生已编号为1，2，3，…，195，为了解高三学生的饮食情况，要按1∶5的比例抽取一个样本，若采用系统抽样法进行抽取，其中抽取的3名编号可能是
A.3，24，33 B.31，47，147
C.133，153，193 D.102，132，159
解析：由系统抽样方法，分成39个部分，每部分5个个体，分段间隔k=5，抽取编号相差5的整数倍.
答案：C
6.一个容量为20的样本数据，分组后，组距与频数如下：（10，20］，2；（20，30］，3；（30，40］，4；（40，50］，5；（50，60]，4；（60，70]，2.则样本在（－∞，50]上的频率为
A.5% B.25%
C.50% D.70%
解析：
=
.
答案：D
7.若数据x1，x2，…，xn的平均数为
，方差为s2，则3x1+5，3x2+5，…，3xn+5的平均数和方差分别是
A.，s2 B.3+5，9s2
C.3+5，s2 D.3+5，9s2+30s+25
解析：代入公式易得为B.
答案：B
8.在抽查某产品的尺寸的过程中，将其尺寸分成若干组，［a，b］是其中一组，抽查出的个数在该组上的频率为m，该组上的直方图的高为h，则a－b等于
A.h·m B.
C.
D.与m、h无关
解析：a－b即为组距，m=hx.
答案：C
9.从107名学生中，采用系统抽样法抽取10名学生作为样本，则每名学生被抽到的概率为
A.
B.
C.
D.
解析：p=
×
=.
答案：D
10.已知样本容量为30，在样本频率分布直方图中，各小长方形的高之比为AE∶BF∶CG∶DH=2∶4∶3∶1，则第2组的频率和频数分别为
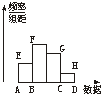
A.0.4，12 B.0.6，16 C.0.4，16 D.0.6，12
解析：频数n2=30×
=12，频率f2=
=0.4.
答案：A
11.将容量为100的样本数据，按由小到大排列分成8个组如下表：
| 组 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频 数 | 10 | 13 | 14 | 14 | 15 | 13 | 12 | 9 |
第三组的频率和累积频率分别为
A.0.14和0.37
B.
和
C.0.03和0.06
D.
和
解析：
=0.14，
=
=0.37.
答案：A
12.在100个零件中，有一级品20个、二级品30个、三级品50个，从中抽取20个作为样本.
①采用随机抽样法将零件编号为00，01，…，99，抽签取出20个；
②采用系统抽样法，将所有零件分成20组，每组5个，然后每组中随机抽取1个；
③采用分层抽样法，从一级品中随机抽取4个，从二级品中随机抽取6个，从三级品中随机抽取10个.
对于上述问题，下面说法正确的是
A.不论采用哪一种抽样方法，这100个零件中每一个被抽到的概率都是
B.①②两种抽样方法，这100个零件中每一个被抽到的概率为，③并非如此
C.①③两种抽样方法，这100个零件中每一个被抽到的概率为，②并非如此
D.采用不同的抽样方法，这100个零件中每一个零件被抽到的概率是各不相同的
解析：依据抽样方法的基本原理知选A.
答案：A
二、填空题（每小题4分，共16分）
13.利用简单随机抽样法，从n个个体（n>13）中抽取13个个体，若第二次抽取时，余下的每个个体被抽取到的概率为
，则在整个抽样过程中，各个个体被抽取到的概率为___________.
解析：第二次抽取时，余下的每个个体被抽到的概率为，所以余下的人数为36人.所以n=37.则在整个抽样过程中，各个个体被抽取到的概率为
.
答案：
14.某公司生产三种型号的轿车，产量分别为1200辆，6000辆和2000辆，为检验该公司的产品质量，现用分层抽样法抽取46辆进行检验，这三种型号的轿车依次应抽取_______辆、_______辆、_______辆.
答案：6 30 10
15.容量为100的某个样本数据拆分为10组，并填写频率分布表，若前七组频率之和为0.79，而剩下的三组的频率成公差为0.05的等差数列，则剩下的三组中频率最大的一组的频率为___________.
解析：依题意，剩下三组的频率之和为1－0.79=0.21，∴0.21=a1+a1+d+a1+2d=3a1+0.15.得a1=0.02.∴频率最大的一组的频率为0.02+2×0.05=0.12.
答案：0.12
16.从甲、乙两个总体中各抽取了一个样本：
甲：900，920，900，850，910，920；
乙：890，960，950，850，860，890.
总体波动较小的是___________.
解析：甲=
（0+20+0－50+10+20）+900=900，
乙=（－10+60+50－50－40－10）+900=900，
s甲2=［（900－900）2+（920－900）2+…+（920－900）2］=
≈567，
s乙2=［（890－900）2+（950－900）2+…+（890－900）2］=
≈1733.
∴波动较小的是甲.
答案：甲
三、解答题（本大题共6小题，共74分）
17.（12分）一个城市有210家商店，其中大型商店有20家，中型商店有40家，小型商店有150家，为掌握各商店的营业情况，要从中抽取一个容量为21的样本，按照分层抽样法抽取样本时，各类商店要抽多少家？写出抽样过程.
解：抽样比为
=，20×=2，40×=4，150×=15，
∴大、中、小型商店各抽2家、4家、15家.
抽样过程：从20家大型商店中随机抽2家，从40家中型商店中随机抽4家，从150家小型商店中随机抽15家，将此21家商店综合在一起即为样本.
18.（12分）某文艺团体演职人员共100人，其中乐队15人，歌队20人，曲艺队30人，舞队25人，职员10人.
（1）列出各队的频率分布表；
（2）画出频率分布条形图.
解：（1）频率分布表如下.
| 队 号 | 1 | 2 | 3 | 4 | 5 |
| 频 数 | 15 | 20 | 30 | 25 | 10 |
| 频 率 | 0.15 | 0.2 | 0.3 | 0.25 | 0.1 |
（2）频率分布条形图如下：
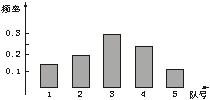
19.（12分）某班有50名学生（男生30名，女生20名），现调查平均身高，准备抽取，问应如何抽样？如果已知男、女生身高有显著差异，又应如何抽样？
解：（1）运用简单随机抽样方法从50名学生中抽取5名学生作为样本.
（2）若男、女生身高有显著差异，则运用分层抽样法抽样，分别运用简单随机抽样法从30名男生中抽取3名，从20名女生中抽取2名，将这5名学生组成样本即为所求.
20.（12分）已知一个样本：25，21，23，25，27，29，25，28，30，29，26，24，25，27，26，22，24，25，26，28.以2为组距，列出频率分布表，并绘出频率分布直方图，并估计样本值出现在22～28之间的概率.
解：可知最大值为30，最小值为21，组距为2，所以可分5组.
频率分布表如下.
| 分 组 | 个数累计 | 频 数 | 频 率 |
| ［20.5，22.5) |
| 2 | 0.10 |
| ［22.5，24.5) |
| 3 | 0.15 |
| ［24.5，26.5) | 正 | 8 | 0.40 |
| ［26.5，28.5) |
| 4 | 0.20 |
| ［28.5，30.5) |
| 3 | 0.15 |
频率分布直方图如下.
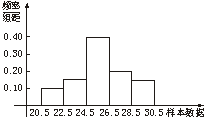
样本值出现在22～28之间的概率为0.75.
21.（12分）有一容量为50的样本，数据的分组及各组的频数如下：
| 分 组 | 频 数 | 频 率 | 累积频率 |
| ［12.5，15.5) | 3 | ||
| ［15.5，18.5) | 8 | ||
| ［18.5，21.5) | 9 | ||
| ［21.5，24.5) | 11 | ||
| ［24.5，27.5) | 10 | ||
| ［27.5，30.5) | 5 | ||
| ［30.5，33.5) | 4 | ||
| 合 计 | 50 |
（1）完成样本的频率分布表（含累积频率）；
（2）画出频率分布直方图和累积频率分布图；
（3）根据累积频率分布图估计小于30的数据约占多大百分比.
解：（1）频率分布表如下：
| 分 组 | 频 数 | 频 率 | 累积频率 |
| ［12.5，15.5) | 3 | 0.06 | 0.06 |
| ［15.5，18.5) | 8 | 0.16 | 0.22 |
| ［18.5，21.5) | 9 | 0.18 | 0.40 |
| ［21.5，24.5) | 11 | 0.22 | 0.62 |
| ［24.5，27.5) | 10 | 0.20 | 0.82 |
| ［27.5，30.5) | 5 | 0.10 | 0.92 |
| ［30.5，33.5) | 4 | 0.08 | 1.00 |
| 合 计 | 50 | 1.00 |
（2）频率分布直方图如下：
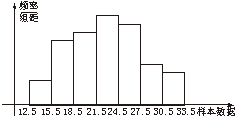
累积频率分布图如下：
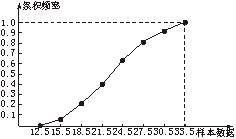
（3）由累积频率分布图可得约占90%.
22.（14分）在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按照5天一组分组统计，绘制了频率分布直方图（如下图）.已知从左到右各长方形的高的比为2∶3∶4∶6∶4∶1，第三组的频数为12，请解答下列各题.
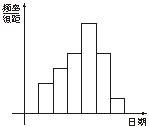
（1）本次活动共有多少件作品参加评比？
（2）哪组上交的作品数量最多？有多少件？
（3）经过评比，第四组和第六组分别有10件、2件作品获奖，问这两组哪一组获奖率较高？
解：（1）依题意可算出第三组的频率为
=.
设共有n件作品，则
=，∴n=60（件）.
（2）由直方图，可看出第四组上交作品数量最多，共有60×
=18（件）.
（3）第四组获奖率为
=
，
第六组获奖率为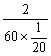
=
=
，
所以第六组获奖率较高.
●意犹未尽
自己救自己
某人在屋檐下躲雨，看见观音正撑伞走过.这人说：“观音菩萨，普度一下众生吧，带我一段如何？”观音说：“我在雨里，你在檐下，而檐下无雨，你不需要我度.”这人立刻跳出檐下，站在雨中：“现在我也在雨中了，该度我了吧？”观音说：“你在雨中，我也在雨中，我不被淋，因为有伞；你被雨淋，因为无伞，所以不是我度自己，而是伞度我.你要想度，不必找我，请自找伞去！”说完便走了.第二天，这人遇到了难事，便去寺庙里求观音.走进庙里，才发现观音的像前也有一个人在拜，那个人长得和观音一模一样，丝毫不差.这人问：“你是观音吗？”那人答道：“我正是观音.”这人又问：“那你为何还拜自己？”观音笑道：“我也遇到了难事，但我知道，求人不如求己.”
一语中的：成功者自救.