福州三中数学模拟试卷(理)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题共60分)
参考公式:
如果事件![]() 、
、![]() 互斥,那么
互斥,那么![]()
如果事件![]() 、
、![]() 相互独立,那么
相互独立,那么![]() ·
·![]() ·
·![]()
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么它在
,那么它在![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
次的概率![]()
球的表面积公式![]() ,其中
,其中![]() 表示球的半径.
表示球的半径.
球的体积公式![]() ,其中
,其中![]() 表示球的半径.
表示球的半径.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如果全集![]() 则
则![]() 等于 ( )
等于 ( )
A.![]() B.(2,4) C.
B.(2,4) C.![]() D.
D.![]()
2.已知角![]() 的终边经过点
的终边经过点![]() ,且
,且![]() ,则
,则![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3.如果向量 ![]() 与
与![]() 共线且方向相反,则
共线且方向相反,则![]() = ( )
= ( )
A.±2 B.-2 C.2 D.0
4.若不等式2x-3>4与不等式x2+px+q>0的解集相同,则![]() = ( )
= ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.设有如下三个命题:甲:相交直线![]() 、m都在平面α内,并且都不在平面β内;乙:直线
、m都在平面α内,并且都不在平面β内;乙:直线![]() 、m中至少有一条与平面β相交;丙:平面α与平面β相交.当甲成立时, ( )
、m中至少有一条与平面β相交;丙:平面α与平面β相交.当甲成立时, ( )
A、乙是丙的充分而不必要条件 B、乙是丙的必要而不充分条件
C、乙是丙的充分且必要条件 D、乙既不是丙的充分条件又不是丙的必要条件
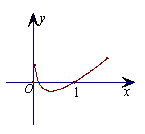
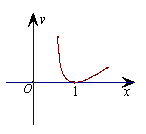
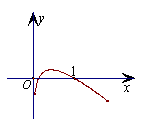
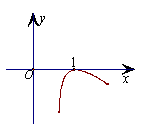 6.函数
6.函数![]() 的图象大致形状是 (
)
的图象大致形状是 (
)
A. B. C. D.
7.要从10名男生和5名女生中选出6人组成啦啦队,若按性别依比例分层抽样且某男生担任队长,则不同的抽样方法数是 ( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若直线mx+ny=4和⊙O∶![]() 没有交点,则过(m,n)的直线与椭圆
没有交点,则过(m,n)的直线与椭圆![]() 的
的
交点个数为( )
A.至多一个 B.2个 C.1个 D.0个
9.数列![]() 是其前n项的和,当
是其前n项的和,当![]() 时,
时,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知函数f(x)是偶函数,且当![]() 时,f(x)=x-1,则不等式f(x-1)<0的解集为( )
时,f(x)=x-1,则不等式f(x-1)<0的解集为( )
A.(-1,0) B. (-∞,0)∪(1,2) C.(0,2) D.(1,2)
 11.如图,建筑工地有一用细砂堆成的多面体,其上下两个底面平行且都是矩形,上底面矩形的两边分别为6米与3米,下底面矩形的
11.如图,建筑工地有一用细砂堆成的多面体,其上下两个底面平行且都是矩形,上底面矩形的两边分别为6米与3米,下底面矩形的
长边为10米,若此多面体的四个侧面与底
面所成的二面角都相等,则其下底面的短边
边长为 ( )
A.7米 B.6米
C.5米 D.4米
12.若函数![]() 在
在![]() 上可导且满足不等式
上可导且满足不等式![]() 恒成立,且常数
恒成立,且常数![]() 满足
满足![]() ,则下列不等式一定成立的是
( )
,则下列不等式一定成立的是
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
第Ⅱ卷 (非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.设![]() 展开式中的第4项是
.
展开式中的第4项是
.
14.双曲线![]() 的两焦点为F1,F2,P在双曲线上,且满足PF1+PF2=
的两焦点为F1,F2,P在双曲线上,且满足PF1+PF2=![]() 则△PF1F2的面积为
则△PF1F2的面积为
15.已知实数x,y满足约束条件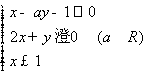 ,目标函数
,目标函数![]() 只有当
只有当![]() 时取得最大值,则
时取得最大值,则![]() 的取值范围是
.
的取值范围是
.
 16.“神六”上天并顺利返回,让越来越多的青少
16.“神六”上天并顺利返回,让越来越多的青少
年对航天技术发生了兴趣。我校的科技小组在
计算机上模拟航天器变轨返回试验,设计方案
如图:航天器运行(按顺时针方向)的轨迹方
程为![]() =1,变轨(航天器运行轨迹
=1,变轨(航天器运行轨迹
由椭圆变为抛物线)后返回的轨迹是以y轴为
对称轴、M(0,![]() )为顶点的抛物线的实线部分,
)为顶点的抛物线的实线部分,
降落点为D(8,0),观测点A(4,0)、B(6,0)同时跟踪
航天器。试问:当航天器在x轴上方时,观测点A、B测得离航天器的距离分别为
___ ______________________时航天器发出变轨指令。
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题12分)
某中学有5名体育类考生要到某大学参加体育专业测试,学校指派一名教师带队,已知每位考生测试合格的概率都是![]() ,
,
(1)若他们乘坐的汽车恰好有前后两排各3个座位,求体育教师不坐后排的概率;
(2)若5人中恰有r人合格的概率为![]() ,求r的值;
,求r的值;
(3)记测试合格的人数为![]() ,求
,求![]() 的期望和方差。
的期望和方差。
18.(本小题12分)
设向量![]()
(1)若![]() ,求
,求![]() 的值.
的值.
(2)记向量![]() 所在的直线的倾斜角为
所在的直线的倾斜角为![]() ,求证:
,求证:![]()
(3)在(2)的条件下,求函数![]() 的值域。
的值域。
19.(本小题满分12分)
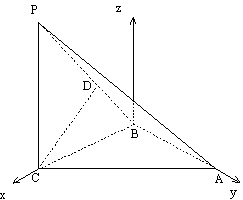
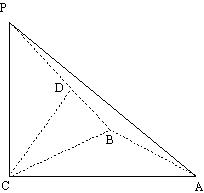 如图,三棱锥P—ABC中, PC
如图,三棱锥P—ABC中, PC![]() 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD![]() 平面PAB.
平面PAB.
(1) 求证:AB![]() 平面PCB;
平面PCB;
(2) 求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B的大小.
20.(本小题12分)
已知数列![]() 、
、![]() 满足:
满足:![]() 为常数),且
为常数),且![]() ,其中
,其中![]() …
…
(Ⅰ)若{an}是等比数列,试求数列{bn}的前n项和![]() 的表达式;
的表达式;
(Ⅱ)当{bn}是等比数列时,甲同学说:{an}一定是等比数列;乙同学说:{an}一定不是等比数列,你认为他们的说法是否正确?为什么?
21.(本小题12分)
设函数![]() (n∈N),且当x=
(n∈N),且当x=![]() 时,f(x)的值为17+12
时,f(x)的值为17+12![]() ;
;![]() (a≠1,a∈R),定义:
(a≠1,a∈R),定义:![]() =
=![]()
![]() -
-![]()
![]() .
.
(1)当a =-1时,![]() 的表达式.
的表达式.
(2)当x ∈[0,1]时,
![]() 的最大值为-65,求a的值.
的最大值为-65,求a的值.
22.(本小题满分14分)
在直角坐标平面上,O为原点,M为动点,![]() ,
,![]() .过点M作MM1⊥
.过点M作MM1⊥![]() 轴于M1,过N作NN1⊥
轴于M1,过N作NN1⊥![]() 轴于点N1,
轴于点N1,![]() .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线![]() 交曲线C于两个不同的点P、Q(点Q在A与P之间).
交曲线C于两个不同的点P、Q(点Q在A与P之间).
(1) 求曲线C的方程;
(2) 证明不存在直线![]() ,使得
,使得![]() ;
;
(3) 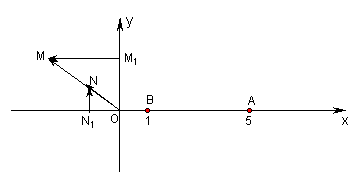 过点P作
过点P作![]() 轴的平行线与曲线C的另一交点为S,若
轴的平行线与曲线C的另一交点为S,若![]() ,证明
,证明![]() .
.
福州三中数学模拟试卷(理)答案
一、选择题:
1.A 2.D 3.B 4.C 5.C 6.A 7.D 8.B 9.A 10. C 11. A 12. B
二、填空题:
13.-35i 14.1 15.![]() 16.
16.![]() ,4
,4
三、解答题
17.解:(1)体育教师不坐后排记为事件A,则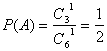 。
。
(2)每位考生测试合格的概率![]() ,测试不合格的概率为
,测试不合格的概率为![]()
则![]() ,即
,即![]() ,
,
∴![]() ,
,![]()
(3)∵![]() ~
~![]() ∴
∴ ![]()
![]()
18.解:(1)![]() ,
,![]() 又
又![]() ,故
,故![]()
(2)![]() ,
,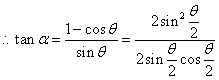
=![]() ,又
,又![]() [0,
[0,![]() ),
),![]() ,
,![]()
(3)将原函数化简得![]() ,由
,由![]() 及
及![]()
可知![]() 故
故![]() ,于是
,于是![]() ]
]
19.解法一:(1) ∵PC![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
∴PC![]() AB.
AB.
 ∵CD
∵CD![]() 平面PAB,
平面PAB,![]() 平面PAB,
平面PAB,
∴CD![]() AB.
AB.
又![]() ,
,
∴AB![]() 平面PCB.
平面PCB.
(2) 过点A作AF//BC,且AF=BC,连结PF,CF.
则![]() 为异面直线PA与BC所成的角.
为异面直线PA与BC所成的角.
由(1)可得AB⊥BC,
∴CF![]() AF.
AF.
由三垂线定理,得PF![]() AF.
AF.
则AF=CF=![]() ,PF=
,PF=![]() ,
,
在![]() 中, tan∠PAF=
中, tan∠PAF=![]() =
=![]() ,
,
∴异面直线PA与BC所成的角为![]() .
.
(3)取AP的中点E,连结CE、DE.
∵PC=AC=2,∴CE ![]() PA,CE=
PA,CE=![]() .
.
∵CD![]() 平面PAB,
平面PAB,
由三垂线定理的逆定理,得 DE ![]() PA.
PA.
∴![]() 为二面角C-PA-B的平面角.
为二面角C-PA-B的平面角.
由(1) AB![]() 平面PCB,又∵AB=BC,可求得BC=
平面PCB,又∵AB=BC,可求得BC=![]() .
.
在![]() 中,PB=
中,PB=![]() ,
,
![]() .
.
 在
在![]() 中, sin∠CED=
中, sin∠CED=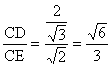 .
.
∴二面角C-PA-B的大小为arcsin![]() .
.
解法二:(1)同解法一.
(2) 由(I) AB![]() 平面PCB,∵PC=AC=2,
平面PCB,∵PC=AC=2,
又∵AB=BC,可求得BC=![]() .
.
以B为原点,如图建立坐标系.
则A(0,![]() ,0),B(0,0,0),
,0),B(0,0,0),
C(![]() ,0,0),P(
,0,0),P(![]() ,0,2).
,0,2).
![]() ,
,![]() .
.
则![]() +0+0=2.
+0+0=2.
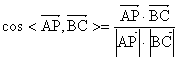 =
=![]() =
= ![]() .
.
∴异面直线AP与BC所成的角为![]() .
.
(3)设平面PAB的法向量为m= (x,y,z).
![]() ,
,![]() ,
,
则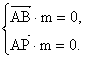 即
即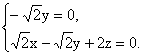
![]()
解得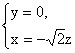 令
令![]() = -1, 得 m= (
= -1, 得 m= (![]() ,0,-1).
,0,-1).
设平面PAC的法向量为n=(![]() ).
).
![]() ,
,![]() ,
,
则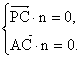 即
即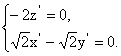
解得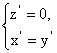 令
令![]() =1, 得 n= (1,1,0).
=1, 得 n= (1,1,0).
![]() =
=![]() .
.
∴二面角C-PA-B的大小为arccos![]() .
.
20. (I)解:因为{an}是等比数列a1=1,a2=a.
∴a≠0,an=an-1.
又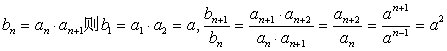
即![]() 是以a为首项, a2为公比的等比数列.
是以a为首项, a2为公比的等比数列.
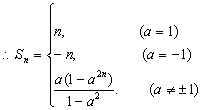
(II)甲、乙两个同学的说法都不正确,理由如下:
解法一:设{bn}的公比为q,则![]()
又a1=1,a2=a, a1, a3, a5,…,a2n-1,…是以1为首项,q为公比的等比数列,
a2, a4, a6, …, a2n , …是以a为首项,q为公比的等比数列,
即{an}为:1,a, q, aq , q2, aq2,
当q=a2时,{an}是等比数列;
当q≠a2时,{an}不是等比数列.
解法二:{an}可能是等比数列,也可能不是等比数列,举例说明如下:
设{bn}的公比为q
(1)取a=q=1时,an=1(n∈N),此时bn=anan+1=1, {an}、{bn}都是等比数列.
(2)取a=2, q=1时,
所以{bn}是等比数列,而{an}不是等比数列.
21. 解:∵f(x)=(x +1)![]() , f(
, f(![]() )= 17+12
)= 17+12![]() , ∴n= 4
, ∴n= 4
又∵![]() , ∴m= 4, ∴F(x)=(x+1)
, ∴m= 4, ∴F(x)=(x+1)![]() -(x+a)
-(x+a)![]()
(1)当a =-1时,F(x)=(x +1)![]() -(x +a)
-(x +a)![]() =8x
=8x![]() +8x
+8x
(2)∵![]()
∴F![]() (x)=12(1-a)x
(x)=12(1-a)x![]() +12(1-a
+12(1-a![]() )x +4(1-a
)x +4(1-a![]() )
)
若![]() ,则
,则![]() =0,不合题意,故
=0,不合题意,故![]()
∴△=[12(1-a![]() )]
)]![]() -4·12(1-a)·4(1-a
-4·12(1-a)·4(1-a![]() )
)
=-48(1-a)![]() < 0
< 0
Ⅰ)当1-a >0时,![]() ,F(x)为增函数.∵x∈[0,1]
,F(x)为增函数.∵x∈[0,1]
∴F(1)=-65
∴2 ![]() -(1+a)
-(1+a)![]() =-65
=-65
∴1+a=±3 ∴a =-4 a=2(舍去)
Ⅱ) 当1-a <0时,![]() ,F(x)为减函数.
,F(x)为减函数.
∴F(0)=-65
∴1 ![]() -a
-a![]() =-65 ∴a =
=-65 ∴a =![]() a =-
a =-![]() (舍去)
(舍去)
综上:a =![]() 或a =-4
或a =-4
22. 解:(1)解:设点T的坐标为![]() ,点M的坐标为
,点M的坐标为![]() ,则M1的坐标为
,则M1的坐标为![]()
![]() ∴点N的坐标为
∴点N的坐标为![]()
∴N1的坐标为![]() ∴
∴![]()
由![]() 有
有 ![]()
∴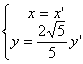 由此得
由此得![]()
由![]() 有
有![]()
∴![]() 即
即![]() ,即为所求的方程.曲线C为椭圆.
,即为所求的方程.曲线C为椭圆.
(2)证:点A(5,0)在曲线C即椭圆的外部,当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 与椭圆C无交点,所以直线
与椭圆C无交点,所以直线![]() 斜率存在,并设为
斜率存在,并设为![]() .直线
.直线![]() 的方程为
的方程为![]() .
.
由方程组 得
得![]()
依题意![]() ,得
,得![]() .
.
当![]() 时,设交点
时,设交点![]() ,PQ的中点为R
,PQ的中点为R![]() ,则
,则
![]() ,
,
![]()
∴![]()
又![]()
![]() BR⊥
BR⊥![]()
![]()
![]()
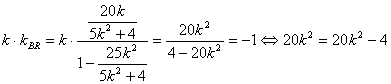
但![]() 不可能成立,所以不存在直线
不可能成立,所以不存在直线![]() 使得
使得![]() .
.
(3)证明:由题有S![]() ,
,![]() .
.
则有方程组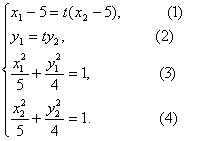
由(1)得:![]()
将(2)、(5)代入(3)有![]()
整理并将(4)、(5)代入得 ![]()
易知![]() ,解得
,解得![]()
因![]() ,故
,故![]() ,
,![]() ,
,
∴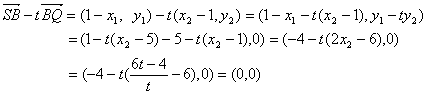
∴![]() .
.