福州三中数学模拟试卷(文)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题共60分)
参考公式:
如果事件![]() 、
、![]() 互斥,那么
互斥,那么![]()
如果事件![]() 、
、![]() 相互独立,那么
相互独立,那么![]() ·
·![]() ·
·![]()
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么它在
,那么它在![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
次的概率![]()
球的表面积公式![]() ,其中
,其中![]() 表示球的半径.
表示球的半径.
球的体积公式![]() ,其中
,其中![]() 表示球的半径.
表示球的半径.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知集合A={x0≤x≤![]() ,x∈Z},集合B={xx=2a,a∈A},则集合A∩B等于 ( )
,x∈Z},集合B={xx=2a,a∈A},则集合A∩B等于 ( )
A.{0,2} B.{0,1} C.{1,2} D.{0}
2. 已知角![]() 的终边经过点
的终边经过点![]() ,且
,且![]() ,则
,则![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3.如果向量 ![]() 与
与![]() 共线且方向相反,则
共线且方向相反,则![]() = ( )
= ( )
A.±2 B.-2 C.2 D.0
4.若不等式2x-3>4与不等式x2+px+q>0的解集相同,则![]() = ( )
= ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.设等差数列{an}前n项和为Sn,则使S6=S7的一组值是 ( )
(A)a3=9, a10=―9 (B)a3=―9,a10= 9
(C)a3=―12, a10=9 (D)a3=―9,a10=12
6.要从10名男生和5名女生中选出6人组成啦啦队,若按性别依比例分层抽样且某男生担任队长,则不同的抽样方法数是 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
7. 椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点![]() 、
、![]() 是它的焦点,长轴长为
是它的焦点,长轴长为![]() ,焦距为
,焦距为![]() ,静放在点
,静放在点![]() 的小球(小球的半径不计),从点
的小球(小球的半径不计),从点![]() 沿直线出发,经椭圆壁反弹后第一次回到点
沿直线出发,经椭圆壁反弹后第一次回到点![]() 时,小球经过的路程是
( )
时,小球经过的路程是
( )
A.![]() B.
B.![]() C.
C.![]() D.以上答案均有可能
D.以上答案均有可能
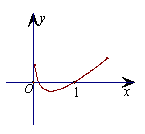
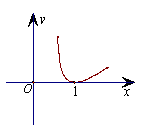
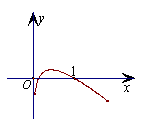
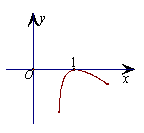 8.函数
8.函数![]() 的图象大致形状是 (
)
的图象大致形状是 (
)
A. B. C. D
9.有以下四个命题:①若直线![]() 是异面直线,
是异面直线,![]() 是异面直线,则
是异面直线,则![]() 是异面直线;②若一条直线与两个平面所成的角相等,则这两个平面平行;③若一个平面内有不共线三个点到另一个平面的距离相等,则这两个平面平行;④三个平面两两相交,有三条交线,则这三条交线一定平行.以上命题中真命题个数有
( )
是异面直线;②若一条直线与两个平面所成的角相等,则这两个平面平行;③若一个平面内有不共线三个点到另一个平面的距离相等,则这两个平面平行;④三个平面两两相交,有三条交线,则这三条交线一定平行.以上命题中真命题个数有
( )
![]() 0个
0个
![]() 1个
1个 ![]() 2个
2个 ![]() 3个
3个
10.已知函数f(x)是偶函数,且当![]() 时,f(x)=x-1,则不等式f(x-1)<0的解集为( )
时,f(x)=x-1,则不等式f(x-1)<0的解集为( )
A.(-1,0) B. (-∞,0)∪(1,2) C.(0,2) D.(1,2)
11. 已知F1、F2为双曲线![]() =1(a>0,b>0)的焦点,过F2作垂直于x轴的直线,它与双曲
=1(a>0,b>0)的焦点,过F2作垂直于x轴的直线,它与双曲
线的一个交点为P,且∠PF1F2=30°,则双曲线的渐近线方程为 ( )
A.y=±![]() x B.y=±
x B.y=±![]() x C.y=±
x C.y=±![]() x D.y=±
x D.y=±![]() x
x
12.若函数![]() 在
在![]() 上是奇函数且可导,若
上是奇函数且可导,若![]() 恒成立,且常数
恒成立,且常数![]() ,则下列不等式一定成立的是
( )
,则下列不等式一定成立的是
( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
第Ⅱ卷 (非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.函数![]() 的定义域为
的定义域为
14.已知球面上A、B两点间的球面距离是1,过这两点的球面半径的夹角为60°,则这个球的表面积与球的体积之比是 .
15.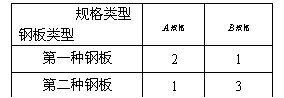 将大小不同的两种钢板截成A、B两种规格的成品,每张钢板可同时截得这两种规格的成品的块数如右表所示.现在需要A、B两种规格的成品分别为12块和10块,则至少需要这两种钢板共 张.
将大小不同的两种钢板截成A、B两种规格的成品,每张钢板可同时截得这两种规格的成品的块数如右表所示.现在需要A、B两种规格的成品分别为12块和10块,则至少需要这两种钢板共 张.
16.请阅读下列命题:
①直线![]() 与椭圆
与椭圆![]() 总有两个交点;
总有两个交点;
②函数![]() 的图象可由函数
的图象可由函数![]() 按向量
按向量![]() 平移得到;
平移得到;
③函数![]() 一定是偶函数;
一定是偶函数;
④抛物线![]() 的焦点坐标是
的焦点坐标是![]() .
.
回答以上四个命题中,真命题是__ _____________(写出所有真命题的编号).
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.
17.(本小题12分)
某中学有5名体育类考生要到某大学参加体育专业测试,学校指派一名教师带队,已知每位考生测试合格的概率都是![]() ,
,
(1)若他们乘坐的汽车恰好有前后两排各3个座位,求体育教师不坐后排的概率;
(2)若5人中恰有r人合格的概率为![]() ,求r的值;
,求r的值;
18. (本小题12分)
设向量![]()
(1)若![]() ,求
,求![]() 的值。
的值。
(2)若![]() ,求向量
,求向量![]() 所在直线的倾斜角
所在直线的倾斜角![]() 的大小。
的大小。
(3)若![]() ,求函数
,求函数![]() 的值域。
的值域。
19.(本小题满分12分)
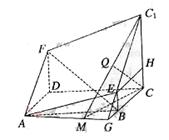
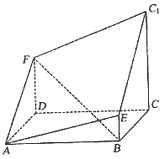 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
(Ⅰ)求证:四边形AEC1F为平行四边形,
(Ⅱ)求BF的长;
(Ⅲ)求点C到平面AEC1F的距离.
20.(本小题满分12分)
已知曲线C:![]() 过点
过点![]() 作C的切线
作C的切线![]() ,切点为P.
,切点为P.
(1)求证:不论![]() 怎样变化,点P总在一条定直线上。
怎样变化,点P总在一条定直线上。
(2)若![]() ,求过P且与
,求过P且与![]() 垂直的直线与
垂直的直线与![]() 轴的交点到原点O的最小距离。
轴的交点到原点O的最小距离。
21.(本小题12分)
已知数列![]() 、
、![]() 满足:
满足:![]() 为常数),且
为常数),且![]() ,其中
,其中![]() …
…
(Ⅰ)若{an}是等比数列,试求数列{bn}的前n项和![]() 的表达式;
的表达式;
(Ⅱ)当{bn}是等比数列时,甲同学说:{an}一定是等比数列;乙同学说:{an}一定不是等比数列,你认为他们的说法是否正确?为什么?
22.(本小题满分14分)
在直角坐标系XOY中,已知点A(1,0),![]() ,C(0,1),
,C(0,1),![]() ,动点M满足
,动点M满足![]() ,其中m是参数(
,其中m是参数(![]() )
)
(Ⅰ)求动点M的轨迹方程,并根据m的取值讨论方程所表示的曲线类型;
(Ⅱ)当动点M的轨迹表示椭圆或双曲线,且曲线与直线![]() 交于不同的两点
交于不同的两点
时,求该曲线的离心率的取值范围.
福州三中数学模拟试卷(文)答案
一、选择题:
1. A 2. D 3. B 4. C 5. C 6. A 7. D 8. A 9. A 10. A 11. D 12. A
二、填空题:
13.![]() 14.
14.![]() 15.7 16.①④
15.7 16.①④
三、解答题:
17. 解:(1)体育教师不坐后排记为事件A,则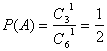 。
。
(2)每位考生测试合格的概率![]() ,测试不合格的概率为
,测试不合格的概率为![]()
则![]() ,(
,(![]() 0,1,2,3,4,5)
0,1,2,3,4,5)
即![]() ,
,
∴![]() ,可得
,可得![]() 或
或 ![]() =4
=4
18.解:(1)![]() ,
,![]() 又
又![]() ,故
,故![]()
(2)![]() ,
,![]()
=![]() ,又
,又![]() [0,
[0,![]() ),
),![]()
(3)将原函数化简得![]() ,由
,由![]() 及
及![]()
可知![]() 故
故![]() ,于是
,于是![]() ]
]
19. 解法1:(Ⅰ)由长方体的性质得平面ADF//平面BC![]() E
E![]()
又![]() 平面AE
平面AE![]() F
F![]() 平面BC
平面BC![]() E=
E=![]() E
E![]()
平面AE![]() F
F![]() 平面ADF=AF
平面ADF=AF
∴AF//![]() E
E![]() 同理AE//
同理AE//![]() F
F
∴四边形AEC1F为平行四边形,
(Ⅱ)过E作EH//BC交CC1于H,则CH=BE=1,EH//AD,且EH=AD.
|
∴Rt△ADF≌Rt△EHC1. ∴DF=C1H=2.
![]()
( Ⅲ)延长C1E与CB交于G,连AG,
则平面AEC1F与平面ABCD相交于AG.
过C作CM⊥AG,垂足为M,连C1M,
由三垂线定理可知AG⊥C1M.由于AG⊥面C1MC,且
AG![]() 面AEC1F,所以平面AEC1F⊥面C1MC.在Rt△C1CM中,作CQ⊥MC1,垂足为Q,则CQ的长即为C到平面AEC1F的距离.
面AEC1F,所以平面AEC1F⊥面C1MC.在Rt△C1CM中,作CQ⊥MC1,垂足为Q,则CQ的长即为C到平面AEC1F的距离.
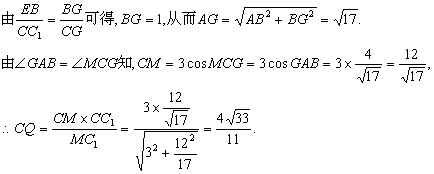
解法2:(Ⅰ)同上
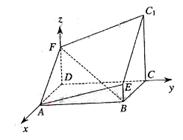
(Ⅱ)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0),A(2,0,0),
C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,z).
|

(Ⅲ)设![]() 为平面AEC1F的法向量,
为平面AEC1F的法向量,
![]()
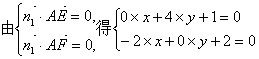
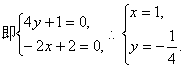 ∴
∴![]()
则C到平面AEC1F的距离为
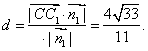
20.证明:(1)设P点的坐标为(![]() ),则
),则
![]() 又
又![]()
则![]() 的斜率为
的斜率为![]() ,
,
又切线过点![]() ,
,
故![]() 的斜率又为
的斜率又为![]() ,
,
即![]()
所以![]() ,所以
,所以![]() ,
,
于是点P总在直线![]() 上.
上.
(2)证法一:直线![]() 的斜率为
的斜率为![]() ,则垂线的斜率为
,则垂线的斜率为![]()
故垂线方程为![]()
令![]() ,解得垂线于
,解得垂线于![]() 轴的交点的坐标为
轴的交点的坐标为
![]()
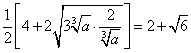 ,
,
当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
所以垂线于![]() 轴的交点到原点O的最小距离为
轴的交点到原点O的最小距离为![]()
证法二:直线![]() 的斜率为
的斜率为![]() ,则垂线斜率为
,则垂线斜率为![]()
垂线方程为![]()
令![]() ,解得垂线于
,解得垂线于![]() 轴的交点的坐标为
轴的交点的坐标为
![]()
= 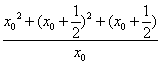
=![]() 2
2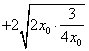
![]() ,
,![]()
当且仅当![]() 即
即![]() 时,等号成立.
时,等号成立.
所以垂线于![]() 轴的交点到原点O的最小距离为
轴的交点到原点O的最小距离为![]() .
.
21.(I)解:因为{an}是等比数列a1=1,a2=a.
∴a≠0,an=an-1.
又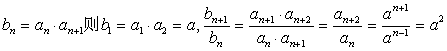
即![]() 是以a为首项, a2为公比的等比数列.
是以a为首项, a2为公比的等比数列.
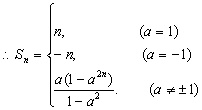
(II)甲、乙两个同学的说法都不正确,理由如下:
解法一:设{bn}的公比为q,则![]()
又a1=1,a2=a, a1, a3, a5,…,a2n-1,…是以1为首项,q为公比的等比数列,
a2, a4, a6, …, a2n , …是以a为首项,q为公比的等比数列,
即{an}为:1,a, q, aq , q2, aq2,
当q=a2时,{an}是等比数列;
当q≠a2时,{an}不是等比数列.
解法二:{an}可能是等比数列,也可能不是等比数列,举例说明如下:
设{bn}的公比为q
(1)取a=q=1时,an=1(n∈N),此时bn=anan+1=1, {an}、{bn}都是等比数列.
(2)取a=2, q=1时,
所以{bn}是等比数列,而{an}不是等比数列.
22.解:(I)设动点M的坐标为(x,y)
由题意得![]()
![]()
![]()
![]()
![]() 动点M的轨迹方程为
动点M的轨迹方程为![]()
当![]() 时,
时,![]() ,即
,即![]() ,动点M的轨迹是一条直线;
,动点M的轨迹是一条直线;
当![]() 时,方程可以化为:
时,方程可以化为:![]()
此时,当![]() 时,动点M的轨迹是一个圆;
时,动点M的轨迹是一个圆;
当![]() ,或
,或![]() 时,动点M的轨迹是一个椭圆
时,动点M的轨迹是一个椭圆
当![]() 时,动点M的轨迹是一条双曲线
时,动点M的轨迹是一条双曲线
(II)当![]() 且
且![]() 时,由
时,由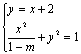 得
得![]()
![]()
![]() 与该圆锥曲线交于不同的两个点
与该圆锥曲线交于不同的两个点
![]()
即![]()
![]() 且
且![]() 或
或![]()
(1)![]() 且
且![]() 时,圆锥曲线表示双曲线
时,圆锥曲线表示双曲线![]()
其中,![]()
![]() 且
且![]()
(2)当![]() 时,该圆锥曲线表示椭圆:
时,该圆锥曲线表示椭圆:![]()
其中![]()
![]()
![]()
综上:该圆锥曲线的离心率e的取值范围是![]()