福州市2003—2004学年第二学期高三质量检查
数学试卷(理科)
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题),全卷满分150分,考试时间120分钟.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率Pn(k)=CnkPk(1-P)n-k
球的表面积公式:S=4πR2,其中R表示球的半径.
球的体积公式:V=![]() πR3,其中R表示球的半径.
πR3,其中R表示球的半径.
第I卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集![]() 则 ( )
则 ( )
A.M∪N=R B.M∩N=![]() C.
C.![]() D.
D.![]()
2.将函数y=sinx按向量![]() =(-
=(-![]() ,3)平移后的函数的解析式为 ( )
,3)平移后的函数的解析式为 ( )
A.y=sin(x-![]() )+3 B.y=sin(x-
)+3 B.y=sin(x-![]() )-3
)-3
C.y=sin(x+![]() )+3 D.y=sin(x+
)+3 D.y=sin(x+![]() )-3
)-3
3.设l、m、n表示三条直线,α、β、γ表示三个平面,则下列命题中不成立的是( )
A.若l⊥α,m⊥α,则l∥m
B.若m![]() β,n是l在β内的射影,m⊥l,则m⊥n
β,n是l在β内的射影,m⊥l,则m⊥n
C.若m![]() α,n
α,n![]() α,m∥n,则n∥α
α,m∥n,则n∥α
D.若α⊥γ,β⊥γ,则α∥β
4.如果数列![]() 是首项为1,公比为2的等比数列,
是首项为1,公比为2的等比数列,
那么![]() = ( )
= ( )
A.2n+1-1 B.2n-1 C.2n-1 D.2n+1
5.已知复数z满足z=1,则z+i的最大值是 ( )
A.0 B.1 C.2 D.3
6.0<x<5是不等式x-2<4成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.有A、B两种类型的车床各一台,现有甲、乙、丙三名工人,其中甲、乙都会操作两种车
床,丙只会操作A种车床,现从这三名工人中选2人分别去操作以上车床,则不同的
选派方法有 ( )
A.6种 B.5种 C.4种 D.3种
8.直线xsinθ+ycosθ=2+sinθ与圆(x-1)2+y2=4的位置关系是 ( )
A.相离 B.相切 C.相交 D.以上都有可能
9.已知x、y满足约束条件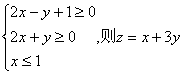 的最小值为 ( )
的最小值为 ( )
A.7 B.![]() C.-5 D.5
C.-5 D.5
|
A.30° B.45°
C.60° D.75°
11.过抛物线y2=4x的焦点的直线交抛物线于A、B两点,
|
A.12 B.-12
C.3 D.-3
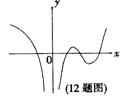
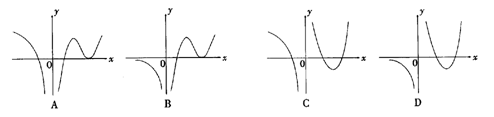
12.设函数f(x)在定义域内可导,y= f(x)的图象如右图所示,
则导函数y= f′(x)的图象可能为 ( )
第Ⅱ卷(非选择题;共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中的横线上.
|
13.一离散型随机变量ξ的概率分布为: 且Eξ=1.5,
则a-b= .
14.正方体的全面积是24cm2,它的顶点都在一个球面上,这个球的表面积是 cm2.
15.已知P是椭圆![]() 上的一点,F1、F2是椭圆的两个焦点,且∠F1PF2=60°,则△F1PF2的面积是
.
上的一点,F1、F2是椭圆的两个焦点,且∠F1PF2=60°,则△F1PF2的面积是
.
16.设![]() 展开式中含x2项的系数,则
展开式中含x2项的系数,则![]() =
=
.
三、解答题:本大题6个小题,共74分.解答题应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知函数![]()
![]() 的大小.
的大小.
18.(本小题满分12分)
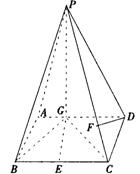
|
(Ⅰ)求异面直线GE与PC所成的角;
(Ⅱ)求点D到平面PBG的距离;
(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求![]() 的值.
的值.
19.(本小题满分12分)
冰箱中放有甲、乙两种饮料各5瓶,每次饮用时从中任意取1瓶甲种或乙种饮料,取用甲种或乙种饮料的概率相等.
(Ⅰ)求甲种饮料饮用完毕而乙种饮料还剩下3瓶的概率;
(Ⅱ)求甲种饮料被饮用瓶数比乙种饮料被饮用瓶数至少多4瓶的概率.
20.(本小题满分12分)
已知数列{an}中,a2=a+2(a为常数);Sn是{an}的前n项和,且Sn是nan与na的等差中项.
(Ⅰ)求a1, a3 ;
(Ⅱ)猜想an的表达式,并用数学归纳法加以证明;
(Ⅲ)求证以![]() 为坐标的点Pn(n=1, 2, …)都落在同一直线上.
为坐标的点Pn(n=1, 2, …)都落在同一直线上.
21.(本小题满分12分)
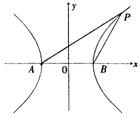
设双曲线C1的方程为![]() ,A、B为其左、右两个顶点,P是双曲线C1上的任意一点,引QB⊥PB,QA⊥PA,AQ与BQ交于点Q.
,A、B为其左、右两个顶点,P是双曲线C1上的任意一点,引QB⊥PB,QA⊥PA,AQ与BQ交于点Q.
|
(Ⅱ)设(I)中所求轨迹为C2,C1、C2
的离心率分别为e1、e2,当![]() 时,e2的取值范围.
时,e2的取值范围.
22.(本小题满分14分)
已知二次函数f(x)=ax2+(a+1)x-a,方程f(x)=0两实根的差的绝对值等于2.
(Ⅰ)求实数a的值.
(Ⅱ)是否存在实数p、q,使得函数F(x)=pf[f(x)]+q f(x),在区间(-∞,-3)内是增函数,在区间(-3,0)内是减函数?若存在,求p、q所要满足的条件;若不存在,说明理由.
福州市2003—2004学年第二学期高三质量检查
数学试卷(理科)参考答案及评分标准
一、选择题
1.B 2.C 3.D 4.B 5.C 6.A 7.C 8.B 9.C 10.B 11.D 12.D
二、填空题
13.0; 14.12π; 15.![]() 16.1.
16.1.
三、解答题
17.解法一:

18.解法一:
(I)由已知![]()
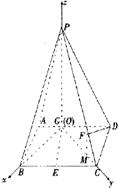 ∴PG=4…………2′
∴PG=4…………2′
如图所示,以G点为原点建立空间直角坐标系o—xyz,
则
B(2,0,0),C(0,2,0),P(0,0,4)
故E(1,1,0)
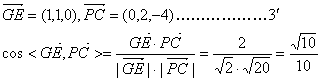
∴异面直线GE与PC所成的角为arccos![]() ……………………4′
……………………4′
(II)平面PBG的单位法向量![]()
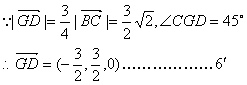
∴点D到平面PBG的距离为![]() ……………………8′
……………………8′
(III)设F(0,y , z)
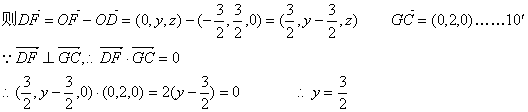
在平面PGC内过F点作FM⊥GC,M为垂足,则![]()
![]() ……………………………………………………………………12′
……………………………………………………………………12′
解法二:
(I)由已知![]()
∴PG=4…………2′
在平面ABCD内,过C点作CH//EG
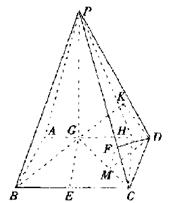 交AD于H,连结PH,则
交AD于H,连结PH,则
∠PCH(或其补角)就是异面直线GE
与PC所成的角.………………3′
在△PCH中,![]()
由余弦定理得,cos∠PCH=![]()
∴异面直线GE与PC所成的角为arccos![]() ……………………4′
……………………4′
(II)∵PG⊥平面ABCD,PG![]() 平面PBG
平面PBG
∴平面PBG⊥平面ABCD
在平面ABCD内,过D作DK⊥BG,交BG延长线于K,则DK⊥平面PBG
∴DK的长就是点D到平面PBG的距离…………………………6′
![]()
在△DKG,DK=DGsin45°=![]()
∴点D到平面PBG的距离为![]() ……………………………………8′
……………………………………8′
(III)在平面ABCD内,过D作DM⊥GC,M为垂足,连结MF,又因为DF⊥GC
∴GC⊥平面MFD, ∴GC⊥FM
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD ∴FM//PG
由GM⊥MD得:GM=GD·cos45°=![]() …………………………10′
…………………………10′
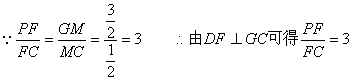 …………12′
…………12′
19.解:(I)由题意知,甲种已饮用5瓶,乙种已饮用2瓶。记“饮用一次,饮用的是甲种饮料”为事件A,则P=P(A)=![]() .题(I)即求7次独立重复试验中事件A发生5次的概率为:
.题(I)即求7次独立重复试验中事件A发生5次的概率为:![]() …………………………6′
…………………………6′
(II)有且仅有3种情形满足要求:
甲被饮用5瓶,乙被饮用1瓶;甲被饮用5瓶,乙没有被饮用;甲被饮用4瓶,乙没有被饮用.……………………………………………………………………8′
所求概率为:P6(5)+P5(5)+P4(4) ………………………………………9′
=C65P5(1-P)+C55P5+C44P4
=![]() …………………………………………………………11′
…………………………………………………………11′
答:甲饮料饮用完毕而乙饮料还剩3瓶的概率为![]() ,甲饮料被饮用瓶数比乙饮料被饮用瓶数至少多4瓶的概率为
,甲饮料被饮用瓶数比乙饮料被饮用瓶数至少多4瓶的概率为![]() .……………………………………12′
.……………………………………12′
20.解:解:(I)由已知得:![]() ………………1′
………………1′
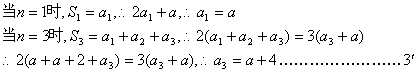
(II)![]() ………4′
………4′
证明:(i)当n=1时,左边=a1=a,右边=a+2(1-1)=a, ∴当n=1时,等式成立
当n=2时,左边=a2=a+2,右边=a+2(2-1)=a+2
∴当n=2时,等式成立.……………………………………………………5′
(ii)假设n=k(k∈N*,k≥2)时,等式成立,即ak=a+2(k-1),
则当n=k+1时
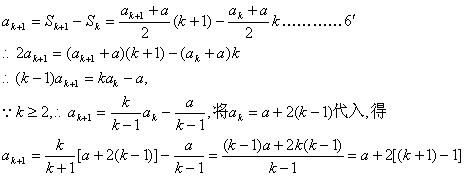
∴当n=k+1时,等式也成立.
由(i)(ii)可知,对任何正整数n,等式![]() 都成立.……………8′
都成立.……………8′
(III)证明当n≥2时,∵an=a+2(n-1)
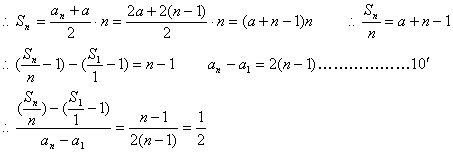
![]() ……)都落在同一直线上.…………………………12′
……)都落在同一直线上.…………………………12′
21.(I)解法一:设P(x0,y0), Q(x ,y )
|

经检验点![]() 不合
不合
因此Q点的轨迹方程为a2x2-b2y2=a4(除点(-a,0),(a,0)外)…………8′
(I)解法二:设P(x0,y0), Q(x,y), ∵A(-a, 0), B(a , 0), QB⊥PB, QA⊥PA
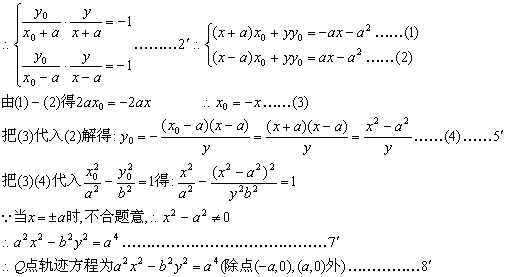
(I)解法三:设P(x0,y0), Q(x,y), ∵PA⊥QA
∴![]() ……(1)…………………………………………1′
……(1)…………………………………………1′
连接PQ,取PQ中点R

22.解:(I)![]()
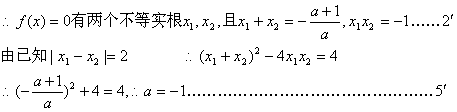
(II)![]() ………………………………6′
………………………………6′
设存在实数p、q满足要求,则
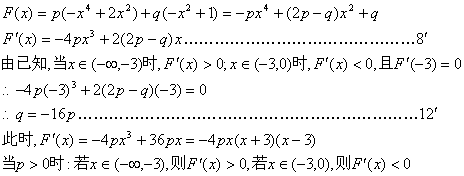
∴存在实数p、q,当p>0且q=-16p时,满足设要求………………14′