 |
数 学 试 卷（文史类）
考试说明：本试卷分第I卷（选择题）第II卷（非选择题）两部分，满分150分。考试时间为120分钟。
以下公式可供解题时参考：如果事件A、B互斥，那么P（A+B）=P（A）+P（B），如果事件互相独立，那么P（A·B）=P（A）·P（B），如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
第Ⅰ卷（选择题，共60分）
一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1．函数y=lg(1－x)(x<0)的反函数是 （ ）
A．y=101－x(x<0) B．y=101－x(x>0)
C．y=1－10x(x<0) D．y=1－10x(x>0)
2．函数
（ ）
A．周期为
的奇函数 B．周期为的偶函数
C．周期2的奇函数 D．周期为2的偶函数
3．设
的值等于 （ ）
A．－
B．－
C． D．
4．正方形ABCD，沿对角线BD折成直二面角后不会成立的结论是 （ ）
A．AC⊥BD B．△ADC为等边三角形
C．AB、CD所成角为60° D．AB与平面BCD所成角为60°
5．已知向量
，则m的值为 （ ）
A．
B．
C．
D．
6．函数
的最大值是 （ ）
A．
B．
C．
D．
7．关于直线a,b,c以及平面M，N，给出下面命题：
①若a//M，b//M, 则a//b ②若a//M,
b⊥M，则b⊥a ③若a
M，bM,且c⊥a，c⊥b,则c⊥M ④若a⊥M, a//N，则M⊥N，其中正确命题的个数为 （ ）
A．0个 B．1个 C．2个 D．3个
8．用四种不同颜色给正方体ABCD—A1B1C1D1的六个面涂色，要求相邻两个面涂不同颜色，则共有涂色方法 （ ）
A．24种 B．72种 C．96种 D．48种
9． 已知a1, a2, a3, a4, a5, a6, a7, a8 各项都大于零的数列，命题①a1, a2, a3, a4, a5, a6, a7, a8不是等比数列；命题②：a1+a8<a4+a5则命题②是命题①的 （ ）
A．充分且必要条件 B．充分但不必要条件
C．必要但不充分条件 D．既不充分也不必要条件
10．一个容量为20的样本数据，分组后，组距与频数如下：
10，20
，2；（20，30，3；（30，40，4；（40，50，5；（50，60，4；（60，70，2；则样本在（50，+∞）上的频率为（ ）
A．
B．
C．
D．
11．点P的曲线
上移动，在点P处的切线的倾斜角为α，则α的取值范围是（ ）
A．
B．
C．
D．
12．直线3x+4y－12=0与椭圆C：
相交于A、B两点，C上点P，使得△PAB的面积等于3，这样的点P共有 （ ）
A．1个 B．2个 C．3个 D．4个
第Ⅱ卷（非选择题，共90分）
二、填空题（本大题共4个小题，每小题4分，共16分）
13．若不等式ax+2<6的解集为（－1，2），则实数a等于
14．把直线
绕点（1，1）顺时针旋转，使它与圆x2+y2－2x=0相切，则直线转动的最小正角是
15．已知
的展开式的第7项为
，则x的值为
16．对于定义域为R的非常值函数f(x)，请将下面左侧中每一个f(x)满足的条件与右侧所提供的f(x)的性质中选择一个用线连接起来
f(x)=－f(－x) f(x)是周期函数
f(x+1)= f(x－1) f(x)是奇函数
f(x+1)= f(1－x) f(x)是偶函数
f(x+y)+ f(x－y)= f(x)f(y) f(x)关于直线x=1对称
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）
17．（本小题满分12分）
已知定义在R上的函数
周期为
（1）写出f(x)的表达式；
（2）写出函数f(x)的单调递增区间；
（3）说明f(x)的图象如何由函数y=2sinx的图象经过变换得到.
18．（本小题满分12分）
已知数列{an}是公比为q的等比数列，Sn是其前n项和，且S3，S9，S6成等差数列
（1）求证：a2 , a8, a5也成等差数列
（2）判断以a2, a8, a5为前三项的等差数列的第四项是否也是数列{an}中的一项，若是求出这一项，若不是请说明理由.
19．（本小题满分12分）
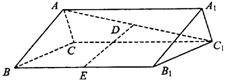
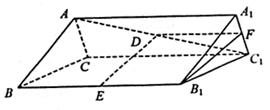
如图，在正三棱柱ABC—A1B1C1中，各棱长都相等，D，E分别为AC1，BB1的中点.
|
（2）求二面角A1—DE—B1的大小.
20．（本小题满分12分）
某职业联赛的总决赛在甲、乙两队之间角逐，采用七局四胜制，即有一队胜四场，则此队获胜，且比赛结束.在每场比赛中，甲队获胜的概率是
乙队获胜的概率是
.根据以往资料统计，每场比赛组织者可获门票收入为30万元，两队决出胜负后，问：
（1）组织者在此决赛中获门票收入为120万元的概率是多少？
（2）组织者在此决赛中获门票收入不低于180万元的概率是多少？
21．（本小题满分12分）
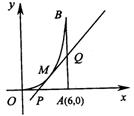
已知定点F（1，0），动点P在y轴上运动，过点P作PM交x轴于点M，并延长MP到点N，且
（1）动点N的轨迹方程；
（2）线l与动点N的轨迹交于A，B两点，若
，求直线l的斜率k的取值范围.
22．（本小题满分14分）
如图所示，曲线段OMB是函数f(x)=x2(0<x<6)的图象，BA⊥x轴于A，曲线段OMB上一点M(t, f(t)处的切线PQ交x轴于P，交线段AB于Q.
（1）试用t表示切线PQ的方程；
（2）设△QAP的面积为g(t)，若函数g(t)在（m , n）上单调递减，试求出m的最小值；
|
，试求出点P横坐标的取值范围.
 |
数 学 试 卷（文科农医类）答案
一、选择题答案
1．D 2．A 3．D 4．D 5．C 6．D 7．C 8．C 9．B 10．C 11．B 12．B
二、填空题答案 13．－4 14．
15．
16．
三、解答题答案
17．（1）
…………………………………………4分
（2）在每个闭区间
…………………………8分
（3）将函数y=2sinx的图象向左平移
个单位，再将得到的函数图象上的所有的点的纵坐标不变，横坐标缩短为原来的………………………………………………12分
18．证明：（1）S3=3a1, S9=9a1, S6=6a1, 而a1≠0，所以S3，S9，S6不可能成等差数列……2分
所以q≠1，则由公式
……4分
即2q6=1+q3 ∴2q6a1q=a1q+q3a1q , ∴2a8=a2+a5 所以a2, a8, a5成等差数列…………6分
（2）由2q6=1+q3=－……………………………………………………………………8分
要以a2, a8, a5为前三项的等差数列的第四项是数列{an}中的第k项，
必有ak－a5=a8－a2,所以
所以
由k是整数，所以
不可能成立，所以a2, a8, a5
为前三项的等差数列的第四项不可能也是数列{an}中的一项.………………………………………………………12分
|
∵D，E分别为AC1和BB1的中点，
∴DF//AA1，DF=AA1
B1E//AA1，B1E=AA1，∴DF//B1E，DF=B1E，∴DEB1F为平行四边形，……………………2分
∴DE//B1F，又∵B1F平面A1B1C1，DE
平面A1B1C1，∴DE//平面A1B1C1.……4分
（2）连结A1D，A1E，在正三棱柱ABC—A1B1C1中，
∵平面A1B1C1⊥平面ACC1A1，A1C1是平面A1B1C1与平面ACC1A1的交线，
又∵B1F平面A1B1C1，且B1F⊥A1C1，∴B1F⊥平面ACC1A1，又DE//B1F，∴DE⊥平面ACC1A1，
∴∠FDA1为二面角A1—DE—B1的平面角，…………8分 并且∠FDA1=∠A1DC1，
设正三棱柱的棱长为1，∵∠AA1C1=90°，D是AC1中点，
∴DC1=
，A1D=，∠A1DC1=90°∴∠FDA1=45°，即二面角A1—DE—B1为45°.………12分
20．（1）①门票收入为120万元的概率为
………………………15分
（2）门票收入不低于180万元的概率
…12分
21．（1）设动点N的坐标为（x,y），则 
…………………2分
，因此，动点的轨迹方程为 
……4分
（2）设l与抛物线交于点A（x1,y1）,B(x2,y2)，当l与x轴垂直时，
则由
， 不合题意，
故与l与x轴不垂直，可设直线l的方程为y=kx+b(k≠0),则由
…6分
由点A，B在抛物线
又y2=4x, y=kx+b得ky2－4y+4b=0,……………………8分
所以
……10分
因为
解得直线l的斜率的取值范围是
.………………………………………………………………12分
22．（1）
………2分
（2）令y=0得
又0<t<6,
∴4<t<6，g(t)在(m, n)上单调递减，故（m, n）
…………8分
（3）当
在（0，4）上单调递增，
∴P的横坐标的取值范围为
.……………………………………………………14分