2005年12月南京江浦中学高三数学月考试卷
一、选择题（本题共12小题，每小题5分，共60分）
1．“x≠2，且y≠3”是“x+y≠5”的 （ ）
A．充分但不必要条件 B．必要但不充分条件
C．充分且必要条件 D．既不充分也不必要条件
2．函数
的图象关于 （ ）
A．直线y=x对称 B．x轴对称 C．y轴对称 D．原点对称
3．下列不等式中成立的是 （ ）
A．
B．
C．
D．
4．设a、b∈R+，则下述不等式中不正确的是 （ ）
A．
B．
C．
D．
5．已知点A（2，—3），B（—3，—2），直线
过点P（1，1）且与线段AB相交，则的斜率k的取值范围是 （ ）
A．
B．
C．
或
D．
或
6．把函数
的图象沿向量
平移后得到函数
的图象，则向量
是 （ ）
A．
B．
C．
D．
7．在等差数列{an}中，已知
则
等于 （ ）
A．45 B．50 C．55 D．60
8．已知公差
等差数列{an}共有m项，am=19，前m项的和Sm=99，则项数m为（ ）
A．7或9 B．7或10 C．8或10 D．9或11
9．去年一辆自行车卖360元，自行车雨衣卖40元，假设今年这种自行车涨价5%，而雨衣降价20%，则今年买同样一辆自行车和一件雨衣要比去年 （ ）
A．多花费2.5% B．多花费3.2% C．少花费4.5% D．少花费1.5%
10．已知函数
，函数
的图象与
的图象关于直线y=x
对称，则g（11）等于 （ ）
A．
B．
C．
D．
11．椭圆的焦点在x轴上，中心在原点，F为左焦点，A为左顶点，B1、B分别为上、下顶点，
若直线AB1⊥BF，则椭圆的离心率为 （ ）
A．
B．
C．
D．
12．从一楼到二楼的楼梯有15级台阶，某人从一楼到二楼每步跨1级或跨2级，他想10
步走完，则不同的走法总数为 （ ）
A．252 B．840 C．1260 D．30240
二、填空题（本大题共4小题，每小题4分，共16分）
13．已知向量=（3，4），
⊥且的起点为（1，2），终点为（x，3x），则=
14．设三个实数
等差数列，又m2，1，n2成等比数列，则
等于
．
15．中心在原点，焦点在x轴上的双曲线的一条渐近线为
焦点到渐近线的距离为6，
则该双曲线的方程为 ．
16．已知函数
在区间[0，a]（a＞0）上的最大值是3，最小值是2，则实
数a的取值范围是 ．
三、解答题（共6小题，共74分）
17．已知
求：
的值．
18．△ABC中，已知三边a、b、c成等差数列，
求
的最小值，并确定此时△ABC的形状．
19．已知函数
（
且
，
（Ⅰ）讨论f（x）的奇偶性与单调性；
（Ⅱ）求f（x）的反函数
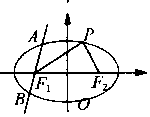（Ⅲ）求使
成立的x的取值范围．
20．已知椭圆C的中点在原点，焦点F1、F2在x轴上，直线过焦点F1且倾角为
，与椭圆C相交于A、B两点，
，点P是椭圆上的动点，
且
的最大值为
，求椭圆C的方程．
21．某大型商厦的家电部计划2002年销售“海豹”牌冰箱2000台，经铁路分若干次等量进货，运输费用按每台50元计算，但每次进货必须另加1万元火车车箱调度费用。冰箱进货后需租用商厦仓库存放，但仓库租用面积必须年前（2001年底）作出计划，租用面积确定以后必须租用一年（中途不能更改租用面积），仓库年租金按所租用面积能存放冰箱的最大数量乘以100元计算．问几次等量进货，才能使运输费用与仓库租金总和最小，最小总费用是多少？
22． 已知数列{an}的首项a1=3，通项an与前n项和Sn之间满足
（Ⅰ）求证：
是等差数列，并求公差；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）数列{an}中是否存在正整数k，使得不等式
对任意不小于k的正整数都成立？若存在，求出最小的k值；若不存在，请说明理由．
答案
一、1．D 2．D 3．D 4．C 5．C 6．D 7． A 8．D 9．A 10．A 11．A 12．A
二、13．
14．—3或1， 15．
16．[1，2]
三、17．由条件得
原式=
18．
等号成立时a=c，∴2a=2b得a=b=c，故
此时△ABC为正三角形．
19．（I）
为奇函数；
任取
，①当
时f（x）为增函数；②当
时f（x）为减函数；
（Ⅱ）
（Ⅲ）①当a＞1时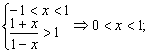
②当0＜a＜1时，
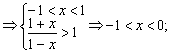
20．设
，等号成立时
，
∴椭圆C方程为
①，而方程为
②，联立①、②得
故椭圆方程为
21．设分n次等量进货，∴总费用
当
时等号成立；而f（4）=f（5）=9；故分4次或5次（最好4次）进货才能使总费用最小，
元．
22．（I）当
时，
（），故
是公差为
的等差数列；（Ⅱ）
得
当时，
而a1=3；
（Ⅲ）
或
∴当k≥3时，恒有
故最小k=3．