中科大附中2005—2006学年度高三试题
数 学
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
第I卷(选择题,共60分)
一、选择题:(题共12小题, 每小题5分,共60分)
1.设全集U![]() , 集合M
, 集合M![]() , N
, N![]() , 那么
, 那么
(CUM)![]() N为 ( )
N为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.等差数列![]() 前四项和为40, 末四项和为72, 所有项和为140, 则该数列共有 ( )
前四项和为40, 末四项和为72, 所有项和为140, 则该数列共有 ( )
A.9项 B.12项 C.10项 D.13项
3.已知平面向量与向量![]() ,
,![]() , 且
, 且![]() , 则
, 则![]() = ( )
= ( )
A.3 B.1
C.-1![]() D.-3
D.-3
4.一平面截一球得到直径是6cm的圆面, 球心到这个平面的距离是4cm , 则该球的体积是
[球的体积公式: ![]() ]
( )
]
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.函数![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6. ![]() 的值是 ( )
的值是 ( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
7.已知抛物线的顶点为原点, 焦点在y轴上, 抛物线上点![]() 到焦点的距离为4, 则m的值为
( )
到焦点的距离为4, 则m的值为
( )
A.4 B.-2 C.4或-4 D.2或-2
8.函数![]() ( )
( )
A.在![]() 内单调递增 B.在
内单调递增 B.在![]() 内单调递减
内单调递减
C.在![]() 内单调递增
D.在
内单调递增
D.在![]() 内单调递减
内单调递减
9.若P![]() 为圆
为圆![]() 的弦AB的中点, 则直线AB的方程是
( )
的弦AB的中点, 则直线AB的方程是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.拟定从甲地到乙地通话m分钟的电话费由![]() (元)决定, 其中
(元)决定, 其中
![]()
![]() 是大于或等于m的最小整数, (如
是大于或等于m的最小整数, (如![]() ), 则从甲地
), 则从甲地
到乙地通话时间为5.5分钟的电话费为 ( )
A.3.71元 B.3.97元 C.4.24元 D.4.77元
11.已知2a+1<0,关于x的不等式![]() 的解集是
( )
的解集是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.设函数![]() ,区间M=[a,b]
,区间M=[a,b]![]() , 集合N={
, 集合N={![]() },
},
则使M=N成立的实数对 (a, b)有 ( )
A.0个 B.1个 C.2个 D.无数多个
第II卷(非选择题,共90分)
二、填空题:(本大题共4小题;每小题4分,共16分)
13.设a、b、c分别是△ABC的∠A、∠B、∠C的对边边长, 则直线![]()
与直线![]() 的夹角大小是
.
的夹角大小是
.
14.已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() , 点P在椭圆上. 若
, 点P在椭圆上. 若![]() 是
是
一个直角三角形的三个顶点, 则点P到x轴的距离为 .
15.已知a、b为不垂直的异面直线, ![]() 是一个平面, 则a、b在
是一个平面, 则a、b在![]() 上的射影有可能是
上的射影有可能是
①两条平行直线 ②两条互相垂直的直线 ③同一条直线 ④一条直线及其外一点称
在上面结论中, 正确结论的编号是 .(写出所有正确结论的编号)
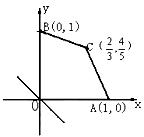 16.给出平面区域如图所示, 目标函数为:
16.给出平面区域如图所示, 目标函数为: ![]()
若当且仅当![]() 时, 目标函数t取最小值,
时, 目标函数t取最小值,
则实数a的取值范围是 .
三、解答题:(本大题6小题,共74分)
17.(本题12分)已知函数![]()
最小正周期![]() .
.
(1) 求实数![]() 的值;
的值;
(2) 若x是![]() 的最小内角, 求函数
的最小内角, 求函数![]() 的值域.
的值域.
18. (本题12分) 解关于![]() 的不等式
的不等式![]() 其中
其中![]() .
.
19.(本题12分) 等差数列![]() 是递增数列,前n项和为
是递增数列,前n项和为![]() , 且
, 且![]() 成等比数列,
成等比数列, ![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() 求数列
求数列![]() 的前99项的和.
的前99项的和.
20. (本题12分)在棱长为4的正方体ABCD—A1B1C1D1中, O是正方形A1B1C1D1的中心, 点
P在棱CC1上, 且CC1=4CP.
(1) 求直线AP与平面BCC1B1所成的角的大小 (结果用反三角函数值表示);
(2) 设O点在平面D1AP上的射影是H, 求证: D1H⊥AP;
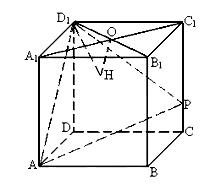 (3) 求点P到平面ABD1的距离.
(3) 求点P到平面ABD1的距离.
21. (本题12分)运货卡车以每小时x千米的速度匀速行驶130千米, 按交通法规限制![]() (单位: 千米/小时). 假设汽油的价格是每升2元, 而汽车每小时耗油
(单位: 千米/小时). 假设汽油的价格是每升2元, 而汽车每小时耗油![]() 升, 司机的工资是每小时14元.
升, 司机的工资是每小时14元.
(1) 求这次行车总费用y关于x的表达式;
(2) 当x为何值时, 这次行车的总费用最低, 并求出最低费用的值.
(精确到小数点后两位,![]() )
)
22.(本题14分)已知双曲线C的中心在原点,抛物线![]() 的焦点是双曲线C的一
的焦点是双曲线C的一
个焦点,且双曲线过点(1, ![]() )
)
(1)求双曲线的方程;
(2)设直线![]() :
:![]() 与双曲线C交于A、B两点, 试问:
与双曲线C交于A、B两点, 试问:
① ![]() 为何值时
为何值时![]()
② 是否存在实数![]() , 使A、B两点关于直线
, 使A、B两点关于直线![]() 对称(
对称(![]() 为常数), 若存在, 求出
为常数), 若存在, 求出![]()
的值; 若不存在, 请说明理由.
数学参考答案
一、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | B | C | D | B | C | A | C | C | A | A |
二、填空题(每小题4分,共16分)
13. ![]() ; 14.
; 14. ![]() ; 15. ① ② ④ ; 16.
; 15. ① ② ④ ; 16. ![]() ;
;
三、解答题(共74分)
17.(本小题满分12分)
解: (1) 因为![]() ………(5分)
………(5分)
所以![]()
![]() .………(6分)
.………(6分)
(2) 因为x是![]() 的最小内角, 所以
的最小内角, 所以![]() ………(8分)
………(8分)
又![]() , 所以
, 所以![]() ………(12分)
………(12分)
18.(本小题满分12分)
解: ∵![]()
![]() ∴
∴ 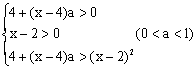 ……(6分)
……(6分)
∴ 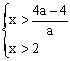 ∴不等式的解集为
∴不等式的解集为![]() ………(12分)
………(12分)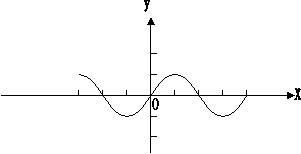
19.(本小题满分12分)
解:(1) 设数列![]() 公差为
公差为![]()
∵![]() 成等比数列 ∴
成等比数列 ∴![]() ………(1分)
………(1分)
![]() ………(3分)
………(3分)
![]() ∵
∵![]() ∴
∴![]() ……… ①………(4分)
……… ①………(4分)
∵![]() ∴
∴![]() ……… ②………(5分)
……… ②………(5分)
由①②得: ![]()
![]() ∴
∴![]() ………(7分)
………(7分)
(2) 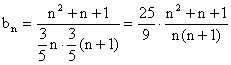
![]() ………(9分)
………(9分)
![]()
![]()
![]() ………(12分)
………(12分)
20.(本小题满分12分)
解:(1)连接BP, ![]() 平面BCC1B1,BP
平面BCC1B1,BP![]() 平面BCC1B1,
平面BCC1B1,
∴![]() BP,
BP, ![]() 为所求的角的平面角, ………(2分)
为所求的角的平面角, ………(2分)
在Rt△ABP中, ![]()
![]() ∴
∴![]() ………(4分)
………(4分)
(2)连接D1B1,A1C1, D1B1⊥A1C1, D1B1⊥A1A, ∴D1B1⊥平面A1A P C1
AP![]() 平面A1A P C1, ∴D1B1⊥AP, ………(5分)
平面A1A P C1, ∴D1B1⊥AP, ………(5分)
又O在平面D1AP上的射影是H ∴OH⊥平面D1AP, AP![]() 平面D1AP
平面D1AP
即OH⊥AP, ………(7分)
得到 AP⊥平面D1OH
, D1H![]() 平面D1OH
平面D1OH
∴AP⊥D1H………(8分)
(3)在平面CC1D1D上作PN∥CD, CD∥AB , 得PN∥AB, ∴PN∥平面ABD1
要求P点到平面ABD1的距离, 即是求N点到平面ABD1的距离.………(9分)
过N点作NM⊥AD1,垂足为M.
|
![]() ………(11分)
………(11分)
![]()
∴点P到平面ABD1的距离是![]() .………(12分)
.………(12分)
21.(本小题满分12分)
解: (1) 设行车所用时间为![]() ………(1分)
………(1分)
![]() ………(5分)
………(5分)
所以, 这次行车总费用y关于x的表达式是
![]()
(或:![]()
![]() ………(7分)
………(7分)
(2)![]() ,
,![]() ………(9分)
………(9分)
仅当![]() 时,
时,
上述不等式中等号成立………(11分)
答:当x约为56.88km/h时, 行车的总费用最低, 最低费用的值约为82.16元.………(12分)
22.(本小题满分14分)
解: (1) 由题意设双曲线方程为![]() ,把(1,
,把(1,![]() )代入得
)代入得![]() (*)………(1分)
(*)………(1分)
又![]() 的焦点是(
的焦点是(![]() ,0),故双曲线的
,0),故双曲线的![]() (2分)与(*)
(2分)与(*)
联立,消去![]() 可得
可得![]() ,
,![]()
∴
![]() ,
,![]() (不合题意舍去)………(3分)
(不合题意舍去)………(3分)
于是![]() ,∴ 双曲线方程为
,∴ 双曲线方程为![]() ………(4分)
………(4分)
(2) 由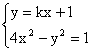 消去
消去![]() 得
得![]() (*),当
(*),当![]()
即![]() (
(![]() )时,
)时,![]() 与C有两个交点A、B………(6分)
与C有两个交点A、B………(6分)
①
设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),因
),因![]() ,故
,故![]() ………(7分)
………(7分)
即![]() ,由(*)知
,由(*)知![]() ,
,![]() ,代入可得
,代入可得
![]() ………(8分)
………(8分)
化简得![]()
∴
![]() ,检验符合条件,故当
,检验符合条件,故当![]() 时,
时,![]() ………(9分)
………(9分)
②
若存在实数![]() 满足条件,则必须
满足条件,则必须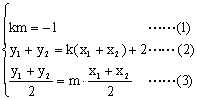 ………(11分)
………(11分)
由(2)、(3)得![]() ………(4)
………(4)
把![]() 代入(4)得
代入(4)得![]() ………(13分)
………(13分)
这与(1)的![]() 矛盾,故不存在实数
矛盾,故不存在实数![]() 满足条件………(14分)
满足条件………(14分)